BITSAT 2016 Question Paper with Answer Key pdf is available for download. BITSAT 2016 was conducted in online CBT mode by BITS Pilani. BITSAT 2016 Question Paper had 150 questions to be attempted in 3 hours.
BITSAT 2016 Question Paper with Answer Key PDF
| BITSAT 2016 Question Paper PDF | BITSAT 2016 Answer Key PDF |
|---|---|
| Download PDF | Download PDF |
What should be the velocity of rotation of earth due to rotation about its own axis so that the weight of a person becomes \( \frac{3}{5} \) of the present weight at the equator. Equatorial radius of the earth is \(6400\,km\).
View Solution
Step 1: Let the angular velocity of earth be \( \omega \).
The apparent weight at the equator is: \[ W' = mg - m\omega^2 R \]
Step 2: Given that the weight becomes \( \frac{3}{5} \) of the original weight: \[ mg - m\omega^2 R = \frac{3}{5}mg \]
Step 3: Simplifying: \[ m\omega^2 R = mg - \frac{3}{5}mg = \frac{2}{5}mg \] \[ \omega^2 = \frac{2g}{5R} \]
Step 4: Substituting values \( g = 9.8\,m/s^2 \), \( R = 6.4 \times 10^6\,m \): \[ \omega^2 = \frac{2 \times 9.8}{5 \times 6.4 \times 10^6} = 6.125 \times 10^{-7} \] \[ \omega = \sqrt{6.125 \times 10^{-7}} \approx 7.8 \times 10^{-4}\,rad/s \] Quick Tip: At the equator, apparent weight decreases due to centrifugal force. Always use: \( W = mg - m\omega^2 R \) for rotating frames.
Block A of mass \(m\) and block B of mass \(2m\) are placed on a fixed triangular wedge by means of a massless, inextensible string and a frictionless pulley as shown in the figure. The wedge is inclined at \(45^\circ\) to the horizontal on both the sides. If the coefficient of friction between block A and the wedge is \( \frac{2}{3} \) and that between block B and the wedge is \( \frac{1}{3} \), and both the blocks A and B are released from rest, the acceleration of A will be:

View Solution
Step 1: Component of weight along incline for A: \[ mg\sin45^\circ = \frac{mg}{\sqrt{2}}, \quad f_A = \mu_A mg\cos45^\circ = \frac{2}{3}\cdot\frac{mg}{\sqrt{2}} \]
Step 2: Net force on A along plane: \[ \frac{mg}{\sqrt{2}} - \frac{2mg}{3\sqrt{2}} = \frac{mg}{3\sqrt{2}} \]
Step 3: For block B: \[ 2mg\sin45^\circ - \mu_B (2mg\cos45^\circ) = \frac{2mg}{\sqrt{2}} - \frac{2mg}{3\sqrt{2}} = \frac{4mg}{3\sqrt{2}} \]
Step 4: The forces balance through the string, hence no net acceleration occurs. Quick Tip: In pulley–incline systems, always compare net driving forces on both sides before assuming motion.
The surface charge density of a thin charged disc of radius \(R\) is \(\sigma\). The value of the electric field at the centre of the disc is \(\frac{\sigma}{2\varepsilon_0}\). With respect to the field at the centre, the electric field along the axis at a distance \(R\) from the centre of the disc:
View Solution
Step 1: Electric field on the axis of a charged disc: \[ E = \frac{\sigma}{2\varepsilon_0}\left(1 - \frac{x}{\sqrt{x^2 + R^2}}\right) \]
Step 2: At \(x = R\): \[ E = \frac{\sigma}{2\varepsilon_0}\left(1 - \frac{1}{\sqrt{2}}\right) \]
Step 3: Fractional reduction: \[ \frac{1}{\sqrt{2}} \approx 0.707 \Rightarrow reduction = 29.3% \] Quick Tip: For discs, remember: centre field is maximum and decreases gradually along the axis.
The molecules of a given mass of a gas have r.m.s. velocity of \(200\,m s^{-1}\) at \(27^\circC\) and \(1.0 \times 10^5\,N m^{-2}\) pressure. When the temperature and pressure of the gas are respectively \(127^\circC\) and \(0.05 \times 10^5\,N m^{-2}\), the r.m.s. velocity of its molecules is:
View Solution
Step 1: RMS velocity depends only on temperature: \[ v_{rms} \propto \sqrt{T} \]
Step 2: Convert temperatures to Kelvin: \[ T_1 = 300\,K, \quad T_2 = 400\,K \]
Step 3: \[ v_2 = 200 \sqrt{\frac{400}{300}} = 200\sqrt{\frac{4}{3}} = 100\sqrt{2} \] Quick Tip: RMS speed is independent of pressure; it depends only on absolute temperature.
An inductor of inductance \(L = 400\,mH\) and resistors of resistance \(R_1 = 2\Omega\) and \(R_2 = 2\Omega\) are connected to a battery of emf \(12\,V\) as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at \(t = 0\). The potential drop across \(L\) as a function of time is:

View Solution
Step 1: Equivalent resistance in series with inductor: \[ R = R_1 + R_2 = 4\Omega \]
Step 2: Time constant: \[ \tau = \frac{L}{R} = \frac{0.4}{4} = 0.1\,s \]
Step 3: Voltage across inductor: \[ V_L = V_0 e^{-t/\tau} = 6e^{-5t}\,V \] Quick Tip: In RL circuits, voltage across the inductor decays exponentially after switching.
Two wires are made of the same material and have the same volume. However wire 1 has cross-sectional area \(A\) and wire 2 has cross-sectional area \(3A\). If the length of wire 1 increases by \(\Delta x\) on applying force \(F\), how much force is needed to stretch wire 2 by the same amount?
View Solution
Step 1: Extension of a wire: \[ \Delta x = \frac{FL}{AY} \]
Step 2: Same volume implies: \[ A_1L_1 = A_2L_2 \Rightarrow L_2 = \frac{L_1}{3} \]
Step 3: For same extension: \[ \frac{F_1L_1}{A_1Y} = \frac{F_2L_2}{A_2Y} \Rightarrow F_2 = 9F_1 \] Quick Tip: For same material, extension depends on \( \frac{FL}{A} \).
Two spheres of different materials, one with double the radius and one-fourth the thickness of the other, are filled with ice. If the time taken for complete melting of the larger sphere is 25 minutes and for the smaller one is 16 minutes, the ratio of thermal conductivities of the materials of the larger sphere to that of the smaller sphere is:
View Solution
Step 1: Heat flow rate: \[ \frac{Q}{t} \propto \frac{kA}{d} \]
Step 2: Time for melting: \[ t \propto \frac{d}{kA} \]
Step 3: Using given ratios and times: \[ \frac{k_L}{k_S} = \frac{t_S}{t_L} \cdot \frac{d_L}{d_S} \cdot \frac{A_L}{A_S} = \frac{16}{25} \cdot \frac{1}{4} \cdot 4 = \frac{5}{4} \] Quick Tip: Melting time increases with thickness and decreases with thermal conductivity.
A biconvex lens has a radius of curvature of magnitude \(20\,cm\). Which of the following options best describe the image formed of an object of height \(2\,cm\) placed \(30\,cm\) from the lens?
View Solution
Step 1: Lens maker formula (assuming glass): \[ \frac{1}{f} = \frac{1}{20} + \frac{1}{20} = \frac{1}{10} \Rightarrow f = 10\,cm \]
Step 2: Lens formula: \[ \frac{1}{v} - \frac{1}{u} = \frac{1}{f} \Rightarrow v = 15\,cm \]
Step 3: Magnification: \[ m = \frac{v}{u} = \frac{15}{30} = \frac{1}{2} \Rightarrow h_i = 1\,cm \] Quick Tip: For convex lenses, objects beyond focus form real, inverted images.
In the figure below, what is the potential difference between the points A and B and between B and C respectively in steady state?

View Solution
Step 1: In steady state, capacitors act as open circuits.
Step 2: Voltage divides equally across equal resistances.
Step 3: Total voltage \(=100\,V\): \[ V_{AB} = V_{BC} = 50\,V \] Quick Tip: In steady state DC, capacitors block current completely.
A radioactive element X converts into another stable element Y. Half-life of X is 2 hours. Initially only X is present. After time \(t\), the ratio of atoms of X and Y is found to be \(1:4\). Then \(t\), in hours is:
View Solution
Step 1: Let initial atoms be \(N_0\).
Step 2: Given ratio: \[ \frac{N_X}{N_Y} = \frac{1}{4} \Rightarrow N_X = \frac{N_0}{5} \]
Step 3: Radioactive decay law: \[ \frac{N_X}{N_0} = \left(\frac{1}{2}\right)^{t/2} = \frac{1}{5} \Rightarrow t \approx 4.6\,h \] Quick Tip: Use decay ratio directly to avoid lengthy calculations.
The approximate depth of an ocean is \(2700\,m\). The compressibility of water is \(45.4 \times 10^{-11}\,Pa^{-1}\) and density of water is \(10^3\,kg m^{-3}\). What fractional compression of water will be obtained at the bottom of the ocean?
View Solution
Step 1: Pressure at depth \(h\): \[ P = \rho g h \]
Step 2: Fractional compression: \[ \frac{\Delta V}{V} = \beta P = \beta \rho g h \]
Step 3: Substituting values: \[ = 45.4\times10^{-11} \times 10^3 \times 9.8 \times 2700 \approx 1.2 \times 10^{-2} \approx 1.4 \times 10^{-2} \] Quick Tip: Fractional compression \(=\beta \rho g h\).
A frictionless wire AB is fixed on a sphere of radius \(R\). A very small spherical ball slips on this wire. The time taken by this ball to slip from A to B is:

View Solution
Step 1: Acceleration along the chord is constant: \[ a = g\cos\theta \]
Step 2: Distance \(AB = 2R\cos\theta\).
Step 3: Time: \[ t = \sqrt{\frac{2s}{a}} = \sqrt{\frac{4R\cos\theta}{g\cos\theta}} = 2\sqrt{\frac{R}{g}} \] Quick Tip: For motion along a chord on a sphere, time is independent of angle.
A string of length \(\ell\) is fixed at both ends. It is vibrating in its 3rd overtone with maximum amplitude \(a\). The amplitude at a distance \(\ell/6\) from one end is:
View Solution
Step 1: 3rd overtone \(= 4^th\) harmonic.
Step 2: Nodes occur at: \[ x = 0, \frac{\ell}{4}, \frac{\ell}{2}, \frac{3\ell}{4}, \ell \]
Step 3: Since \(\ell/6\) lies very close to a node, amplitude is zero. Quick Tip: Amplitude is zero at nodes in standing waves.
A deuteron of kinetic energy \(50\,keV\) is describing a circular orbit of radius \(0.5\,m\) in a plane perpendicular to the magnetic field \(B\). The kinetic energy of the proton that describes a circular orbit of radius \(0.5\,m\) in the same plane with the same \(B\) is:
View Solution
Step 1: Radius of circular motion: \[ r = \frac{mv}{qB} \]
Step 2: For same \(r\) and \(B\): \[ \sqrt{mK} = constant \]
Step 3: Since \(m_d = 2m_p\): \[ K_p = 2K_d = 100\,keV \] Quick Tip: For same radius in magnetic field: \(K \propto \frac{1}{m}\).
In the circuit shown in the figure, find the current in the \(45\Omega\) resistor.

View Solution
Step 1: Reduce the network using symmetry and series–parallel combinations.
Step 2: Equivalent resistance of the network is \(72\Omega\).
Step 3: Total current: \[ I = \frac{180}{72} = 2.5\,A \] Quick Tip: Use symmetry to simplify complex resistor networks.
Kepler's third law states that the square of the period of revolution (\(T\)) of a planet around the sun is proportional to the third power of average distance \(r\) between sun and planet i.e. \(T^2 = Kr^3\), where \(K\) is a constant. If the masses of sun and planet are \(M\) and \(m\) respectively and as per Newton's law of gravitation the force of attraction between them is \(F=\dfrac{GMm}{r^2}\), where \(G\) is the gravitational constant. The relation between \(G\) and \(K\) is described as:
View Solution
Step 1: For circular motion, \[ \frac{GMm}{r^2} = \frac{mv^2}{r} \Rightarrow v^2 = \frac{GM}{r} \]
Step 2: Time period: \[ T = \frac{2\pi r}{v} \Rightarrow T^2 = \frac{4\pi^2 r^3}{GM} \]
Step 3: Comparing with \(T^2 = Kr^3\): \[ K = \frac{4\pi^2}{GM} \Rightarrow GMK = 4\pi^2 \] Quick Tip: Kepler’s third law is a direct consequence of Newton’s law of gravitation.
Find the number of photons emitted per second by a \(25\,W\) source of monochromatic light of wavelength \(6600\,\AA\). What is the photoelectric current assuming \(3%\) efficiency for photoelectric effect?
View Solution
Step 1: Energy of one photon: \[ E = \frac{hc}{\lambda} = \frac{6.6\times10^{-34}\times3\times10^8}{6.6\times10^{-7}} = 3\times10^{-19}\,J \]
Step 2: Number of photons per second: \[ N = \frac{25}{3\times10^{-19}} = \frac{25}{3}\times10^{19}\,s^{-1} \]
Step 3: Photoelectric current (\(3%\) efficiency): \[ I = 0.03\,Ne = 0.03\times\frac{25}{3}\times10^{19}\times1.6\times10^{-19} = 0.4\,A \] Quick Tip: Photon energy depends only on wavelength, not on intensity.
A ray of light of intensity \(I\) is incident on a parallel glass slab at point A as shown in the diagram. It undergoes partial reflection and refraction. At each reflection, \(25%\) of incident energy is reflected. The rays AB and A'B' undergo interference. The ratio of \(I_{\max}\) and \(I_{\min}\) is:

View Solution
Step 1: Reflected intensity \(I_1 = 0.25I\), transmitted intensity \(I_2 = 0.75I\).
Step 2: Amplitudes are proportional to square roots of intensities: \[ a_1 : a_2 = \sqrt{0.25} : \sqrt{0.75} = 1 : \sqrt{3} \]
Step 3: Interference ratio: \[ \frac{I_{\max}}{I_{\min}} = \frac{(a_1+a_2)^2}{(a_2-a_1)^2} = \frac{(1+\sqrt{3})^2}{(\sqrt{3}-1)^2} = 7 \] Quick Tip: For interference: \(I_{\max}/I_{\min} = (a_1+a_2)^2/(a_1-a_2)^2\).
A capillary tube of radius \(r\) is immersed vertically in a liquid such that liquid rises in it to height \(h\) (less than the length of the tube). Mass of liquid in the capillary tube is \(m\). If radius of the capillary tube is increased by \(50%\), then mass of liquid that will rise in the tube is:
View Solution
Step 1: Height of capillary rise: \[ h = \frac{2T\cos\theta}{\rho g r} \]
Step 2: Mass of liquid: \[ m = \rho \pi r^2 h \propto r \]
Step 3: If \(r\) increases by \(50%\): \[ m' = 1.5m = \frac{3}{2}m \] Quick Tip: In capillarity, mass of liquid raised is directly proportional to tube radius.
The drift velocity of electrons in a silver wire with cross–sectional area \(3.14\times10^{-6}\,m^2\) carrying a current of \(20\,A\) is to be calculated. Given: atomic weight of Ag \(=108\), density of silver \(=10.5\times10^3\,kg m^{-3}\).
View Solution
Step 1: Drift velocity formula: \[ v_d = \frac{I}{nqA} \]
Step 2: Number density of electrons: \[ n = \frac{\rho N_A}{M} = \frac{10.5\times10^3 \times 6.02\times10^{23}}{108\times10^{-3}} \]
Step 3: Substituting values: \[ v_d = \frac{20}{n(1.6\times10^{-19})(3.14\times10^{-6})} \approx 6.798\times10^{-4}\,m s^{-1} \] Quick Tip: Drift velocity is extremely small even for large currents.
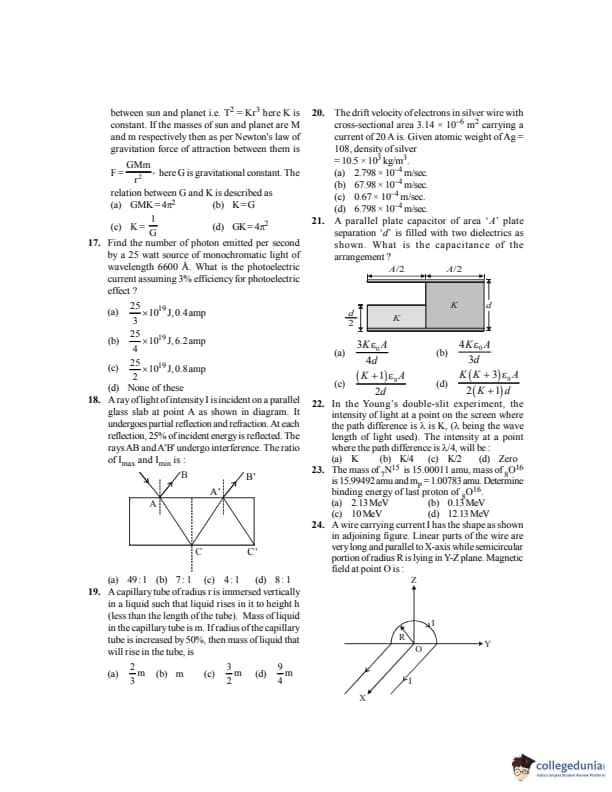
A parallel plate capacitor of area \(A\) and plate separation \(d\) is filled with two dielectrics as shown. What is the capacitance of the arrangement?

View Solution
Step 1: The capacitor behaves as two capacitors in parallel.
Step 2: Capacitances: \[ C_1 = \frac{K\varepsilon_0(A/2)}{d/2}, \quad C_2 = \frac{K\varepsilon_0(A/2)}{d} \]
Step 3: Total capacitance: \[ C = C_1 + C_2 = \frac{3K\varepsilon_0A}{4d} \] Quick Tip: Divide complex dielectric systems into simple series or parallel capacitors.
In Young’s double–slit experiment, the intensity of light at a point on the screen where the path difference is \(K\lambda\) is \(K\) (\(\lambda\) being the wavelength). The intensity at a point where the path difference is \(\lambda/4\) will be:
View Solution
Step 1: Intensity in interference: \[ I \propto \cos^2\left(\frac{\phi}{2}\right) \]
Step 2: For path difference \(\lambda/4\): \[ \phi = \frac{2\pi}{\lambda}\cdot\frac{\lambda}{4} = \frac{\pi}{2} \]
Step 3: \[ I = I_{\max}\cos^2\left(\frac{\pi}{4}\right) = \frac{I_{\max}}{2} \Rightarrow I = \frac{K}{4} \] Quick Tip: Always convert path difference to phase difference first.
The mass of \(^{15}\mathrm{N}\) is \(15.00011\,amu\) and that of \(^{16}\mathrm{O}\) is \(15.99492\,amu\). The mass of the first proton is \(1.00783\,amu\). Determine the binding energy of the last proton of \(^{16}\mathrm{O}\).
View Solution
Step 1: Mass defect: \[ \Delta m = m(^{15}N) + m_p - m(^{16}O) \]
Step 2: \[ \Delta m = 15.00011 + 1.00783 - 15.99492 = 0.01302\,amu \]
Step 3: Binding energy: \[ E = \Delta m \times 931 \approx 2.13\,MeV \] Quick Tip: Binding energy is obtained directly from mass defect.
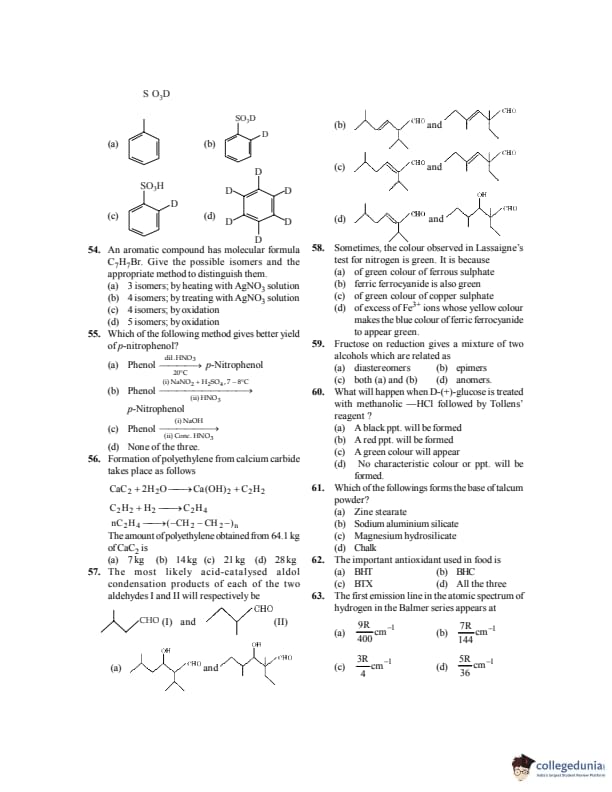
A wire carrying current \(I\) has the shape as shown in the adjoining figure. Linear parts of the wire are very long and parallel to X–axis while the semicircular portion of radius \(R\) lies in Y–Z plane. Magnetic field at point \(O\) is:

View Solution
Step 1: Magnetic field due to semicircular arc: \[ B_{arc}=\frac{\mu_0 I}{4R} \]
Direction is along \(+\hat{i}\).
Step 2: Magnetic field due to two long straight wires: \[ B_{straight}=2\left(\frac{\mu_0 I}{4\pi R}\right) \]
Direction is along \(+\hat{k}\).
Step 3: Net magnetic field: \[ \vec{B}=\frac{\mu_0 I}{4\pi R}(\pi \hat{i}+2\hat{k}) \] Quick Tip: Use right–hand thumb rule separately for curved and straight current elements.
A stone projected with velocity \(u\) at an angle \(\theta\) with the horizontal reaches maximum height \(H_1\). When it is projected with velocity \(u\) at an angle \(\left(\frac{\pi}{2}-\theta\right)\), it reaches maximum height \(H_2\). The relation between the horizontal range \(R\) of the projectile, heights \(H_1\) and \(H_2\) is:
View Solution
Step 1: Maximum heights: \[ H_1=\frac{u^2\sin^2\theta}{2g},\quad H_2=\frac{u^2\cos^2\theta}{2g} \]
Step 2: Horizontal range: \[ R=\frac{u^2\sin2\theta}{g} \]
Step 3: Eliminating \(u\) and \(\theta\): \[ R=4\sqrt{H_1H_2} \] Quick Tip: Complementary angles give same range but different maximum heights.
If the series limit wavelength of the Lyman series for hydrogen atom is \(912\,\AA\), then the series limit wavelength for the Balmer series of hydrogen atom is:
View Solution
Step 1: Lyman series limit corresponds to transition \(n=\infty \to 1\).
Step 2: Balmer series limit corresponds to transition \(n=\infty \to 2\).
Step 3: Since wavelength \(\lambda \propto n^2\): \[ \lambda_{Balmer} = 4\lambda_{Lyman} = 912\times4\,\AA \] Quick Tip: Balmer series wavelengths are four times those of Lyman series.
In the shown arrangement of the meter bridge AC corresponding to null deflection of galvanometer is \(x\). What would be its value if the radius of the wire AB is doubled?

View Solution
Step 1: Resistance of wire: \[ R \propto \frac{1}{r^2} \]
Step 2: Doubling radius makes resistance one–fourth.
Step 3: In meter bridge, balancing length is proportional to resistance: \[ x'=\frac{x}{4} \] Quick Tip: In meter bridge problems, balance length varies directly with resistance.
A \(1\,kg\) mass is attached to a spring of force constant \(600\,N m^{-1}\) and rests on a smooth horizontal surface with other end of the spring tied to a wall as shown in the figure. A second mass of \(0.5\,kg\) slides along the surface with initial speed \(3\,m s^{-1}\). If the masses make a perfectly inelastic collision, then find the amplitude and time period of oscillation of the combined mass.

View Solution
Step 1: Velocity after perfectly inelastic collision: \[ v=\frac{(0.5)(3)}{1+0.5}=1\,m s^{-1} \]
Step 2: Combined mass: \[ M=1.5\,kg \]
Step 3: Angular frequency: \[ \omega=\sqrt{\frac{k}{M}}=\sqrt{\frac{600}{1.5}}=20\,rad s^{-1} \]
Step 4: Amplitude: \[ A=\frac{v}{\omega}=\frac{1}{20}=0.05\,m=5\,cm \]
Step 5: Time period: \[ T=\frac{2\pi}{\omega}=\frac{\pi}{5}\,s \] Quick Tip: After inelastic collision, use conservation of momentum before SHM relations.
The frequency of vibration of a string is given by \[ \nu=\frac{p}{2l}\left[\frac{F}{m}\right]^{1/2} \]
Here \(p\) is number of segments in the string and \(l\) is the length. The dimensional formula for \(m\) will be:
View Solution
Step 1: Dimension of frequency: \[ [\nu]=T^{-1} \]
Step 2: Force: \[ [F]=MLT^{-2} \]
Step 3: From equation: \[ T^{-1}=\left[\frac{F}{m}\right]^{1/2} \Rightarrow m=[ML^{-1}] \] Quick Tip: Always equate dimensions of both sides to find unknown quantities.
For the angle of minimum deviation of a prism to be equal to its refracting angle, the prism must be made of a material whose refractive index:
View Solution
Step 1: Condition: \[ \delta_{\min}=A \]
Step 2: Prism formula: \[ \mu=\frac{\sin\left(\frac{A+\delta_{\min}}{2}\right)}{\sin\left(\frac{A}{2}\right)} \Rightarrow \mu=\frac{\sin A}{\sin(A/2)}=2\cos\frac{A}{2} \]
Step 3: Hence: \[ 1<\mu<\sqrt{2} \] Quick Tip: Minimum deviation equal to prism angle gives a useful refractive index range.
Consider elastic collision of a particle of mass \(m\) moving with a velocity \(u\) with another particle of the same mass at rest. After the collision the projectile and the struck particle move in directions making angles \(\theta_1\) and \(\theta_2\) respectively with the initial direction of motion. The sum of the angles \(\theta_1+\theta_2\) is:
View Solution
Step 1: In elastic collision of equal masses: \[ \vec{v}_1 \perp \vec{v}_2 \]
Step 2: Hence: \[ \theta_1+\theta_2=90^\circ \] Quick Tip: For elastic collision of identical masses, velocities are perpendicular after collision.
A conducting circular loop is placed in a uniform magnetic field of \(0.04\,T\) with its plane perpendicular to the magnetic field. The radius of the loop starts shrinking at \(2\,mm s^{-1}\). The induced emf in the loop when the radius is \(2\,cm\) is:
View Solution
Step 1: Magnetic flux: \[ \Phi=BA=\pi Br^2 \]
Step 2: Induced emf: \[ \mathcal{E}=\left|\frac{d\Phi}{dt}\right|=2\pi Br\frac{dr}{dt} \]
Step 3: Substituting values: \[ \mathcal{E}=2\pi(0.04)(0.02)(2\times10^{-3}) =4.8\pi\,\muV \] Quick Tip: For shrinking loop: \(\mathcal{E}=2\pi Br\,\frac{dr}{dt}\).
Figure below shows two paths that may be taken by a gas to go from a state A to a state C. In process AB, \(400\,J\) of heat is added to the system and in process BC, \(100\,J\) of heat is added to the system. The heat absorbed by the system in the process AC will be:

View Solution
Step 1: From the \(P\!-\!V\) diagram, internal energy change \(\Delta U\) between states A and C is path independent.
Step 2: Along path \(A \to B \to C\): \[ Q_{AB}+Q_{BC}=400+100=500\,J \]
Step 3: Work done: \[ W_{AB}=0 \quad (constant volume) \] \[ W_{BC}=P\,\Delta V = 6\times10^4 \times (4-2)\times10^{-3} = 120\,J \]
Step 4: Change in internal energy: \[ \Delta U = Q - W = 500 - 120 = 380\,J \]
Step 5: Along path \(A \to C\): \[ Q_{AC}=\Delta U + W_{AC} \]
From the diagram, \(W_{AC}=0\), hence \[ Q_{AC}=380\,J \] Quick Tip: Internal energy change depends only on initial and final states, not on the path.
Two resistances at \(0^\circC\) with temperature coefficients of resistance \(\alpha_1\) and \(\alpha_2\) joined in series act as a single resistance in a circuit. The temperature coefficient of their single resistance will be:
View Solution
Step 1: Let resistances at \(0^\circC\) be \(R_1\) and \(R_2\).
Step 2: At temperature \(t\): \[ R = R_1(1+\alpha_1 t)+R_2(1+\alpha_2 t) \]
Step 3: Effective temperature coefficient: \[ \alpha = \frac{R_1\alpha_1+R_2\alpha_2}{R_1+R_2} \]
Step 4: For equal resistances: \[ \alpha=\frac{\alpha_1+\alpha_2}{2} \] Quick Tip: For series combination of equal resistances, temperature coefficient is the average.
Two identical charged spheres suspended from a common point by two massless strings of length \(l\) are initially at a distance \(d \ll l\) apart because of their mutual repulsion. The charges begin to leak from both the spheres at a constant rate. As a result, the spheres approach each other with a velocity \(v\). Then \(v\) varies as a function of distance \(x\) between the spheres as:
View Solution
Step 1: For small angles, equilibrium gives: \[ \frac{kq^2}{x^2} \propto x \Rightarrow q^2 \propto x^3 \]
Step 2: Since charge leaks at constant rate: \[ q \propto t \Rightarrow x^{3/2} \propto t \]
Step 3: Velocity: \[ v=\frac{dx}{dt} \propto x^{-1/2} \] Quick Tip: Use small-angle approximation and equilibrium conditions for charged pendulums.
A point particle of mass \(0.1\,kg\) is executing S.H.M. of amplitude \(0.1\,m\). When the particle passes through the mean position, its kinetic energy is \(8\times10^{-3}\,J\). Obtain the equation of motion of this particle if its initial phase of oscillation is \(45^\circ\).
View Solution
Step 1: Maximum kinetic energy: \[ K_{\max}=\frac{1}{2}m\omega^2A^2 \]
Step 2: Substituting values: \[ 8\times10^{-3}=\frac{1}{2}(0.1)\omega^2(0.1)^2 \Rightarrow \omega=4\,rad s^{-1} \]
Step 3: Equation of motion: \[ y=A\sin(\omega t+\phi)=0.1\sin\left(4t+\frac{\pi}{4}\right) \] Quick Tip: Maximum kinetic energy in SHM occurs at mean position.
A source of sound \(S\) emitting waves of frequency \(100\,Hz\) and an observer \(O\) are located at some distance from each other. The source is moving with a speed of \(19.4\,m s^{-1}\) at an angle of \(60^\circ\) with the source–observer line as shown. The observer is at rest. The apparent frequency observed is (velocity of sound in air \(=330\,m s^{-1}\)):

View Solution
Step 1: Component of source velocity towards observer: \[ v_s=19.4\cos60^\circ=9.7\,m s^{-1} \]
Step 2: Doppler formula: \[ f' = f\frac{v}{v-v_s} =100\frac{330}{330-9.7}\approx103\,Hz \] Quick Tip: Only the component of velocity along the line of sight affects Doppler shift.
A resistor of resistance \(R\), capacitor of capacitance \(C\) and inductor of inductance \(L\) are connected in parallel to an AC power source of voltage \(\varepsilon_0\sin\omega t\). The maximum current through the resistance is half of the maximum current through the power source. Then value of \(R\) is:
View Solution
Step 1: Current through resistor: \[ I_R=\frac{\varepsilon_0}{R} \]
Step 2: Total current: \[ I=\varepsilon_0\sqrt{\left(\frac{1}{R}\right)^2+\left(\omega C-\frac{1}{\omega L}\right)^2} \]
Step 3: Given \(I_R=\frac{I}{2}\): \[ \frac{1}{R}=\frac{1}{2}\sqrt{\left(\frac{1}{R}\right)^2+\left(\omega C-\frac{1}{\omega L}\right)^2} \]
Step 4: Solving: \[ R=\sqrt{3}\left|\frac{1}{\omega C}-\omega L\right| \] Quick Tip: In parallel AC circuits, currents add vectorially, not algebraically.
A lens having focal length \(f\) and aperture of diameter \(d\) forms an image of intensity \(I\). Aperture of diameter \(d/2\) in central region of lens is covered by a black paper. Focal length of lens and intensity of image now will be respectively:
View Solution
Step 1: Focal length depends only on curvature and refractive index.
Step 2: Effective transmitting area reduces by \(1/4\), so remaining area is \(3/4\).
Step 3: Hence intensity: \[ I'=\frac{3I}{4} \] Quick Tip: Blocking part of a lens reduces brightness, not image size or focal length.
A circular disc of radius \(R\) and thickness \(\frac{R}{6}\) has moment of inertia \(I\) about an axis passing through its centre perpendicular to its plane. It is melted and recast into a solid sphere. The moment of inertia of the sphere about its diameter is:
View Solution
Step 1: Volume conservation: \[ \pi R^2\left(\frac{R}{6}\right)=\frac{4}{3}\pi r^3 \Rightarrow r=\frac{R}{2} \]
Step 2: Disc moment of inertia: \[ I=\frac{1}{2}MR^2 \]
Step 3: Sphere moment of inertia: \[ I_s=\frac{2}{5}Mr^2=\frac{2}{5}M\left(\frac{R}{2}\right)^2=\frac{MR^2}{10} \]
Step 4: Hence: \[ I_s=\frac{I}{10} \] Quick Tip: Always conserve mass (or volume) when objects are reshaped.
In \(\mathrm{PO_4^{3-}}\), the formal charge on each oxygen atom and the P–O bond order respectively are:
View Solution
Step 1: Total charge on \(\mathrm{PO_4^{3-}}\) is \(-3\), distributed equally over 4 oxygen atoms.
Step 2: Formal charge on each oxygen: \[ \frac{-3}{4}=-0.75 \]
Step 3: Total P–O bonds \(=5\) (one double bond + three single bonds): \[ Average bond order=\frac{5}{4}=1.25 \] Quick Tip: Average bond order is total bonds divided by number of equivalent bonds.
The decreasing order of the ionization potential of the following elements is:
View Solution
Step 1: Ionization energy increases across a period and decreases down a group.
Step 2: Noble gases have the highest ionization energy.
Step 3: Due to half-filled stability, \(P > S\). Quick Tip: Half-filled and fully filled orbitals have extra stability.
Knowing that the chemistry of lanthanoids (Ln) is dominated by its \(+3\) oxidation state, which of the following statements is incorrect?
View Solution
Step 1: Lanthanoid contraction causes decrease in ionic size.
Step 2: Ln(III) compounds are generally coloured due to f–f transitions.
Step 3: Hence statement (B) is incorrect. Quick Tip: f–f electronic transitions are responsible for colours in lanthanoids.
Which of the following arrangements does not represent the correct order of the property stated against it?
View Solution
Step 1: Ionic size decreases with increasing nuclear charge.
Step 2: Order in option (B) is incorrect. Quick Tip: Higher nuclear charge pulls electrons closer, reducing ionic size.
Which of the following is paramagnetic?
View Solution
Step 1: \(\mathrm{Co^{3+}}\) has \(d^6\) configuration.
Step 2: \(F^-\) is a weak field ligand → high spin complex.
Step 3: Presence of unpaired electrons → paramagnetic. Quick Tip: Weak ligands produce high-spin, paramagnetic complexes.
The hypothetical cis–chloro–diaquatramminecobalt(III) chloride can be represented as:
View Solution
Step 1: Coordination number of Co(III) is 6.
Step 2: Ligands: \(3NH_3 + 2H_2O + 1Cl^-\).
Step 3: Charge balance gives two chloride ions outside the coordination sphere. Quick Tip: Always balance charge inside and outside coordination sphere.
The normality of \(26%\) (w/v) solution of ammonia (density \(=0.855\)) is approximately:
View Solution
Step 1: \(26%\) w/v means \(26\,g\) in \(100\,mL\).
Step 2: Molar mass of \(NH_3 =17\).
Step 3: Molarity: \[ \frac{26/17}{0.1}\approx15.3 \]
Step 4: For monobasic base: \[ N=M=15.3 \] Quick Tip: For acids/bases with valency 1, normality equals molarity.
A \(1.25\,g\) sample of a mixture of \(Na_2CO_3\) and \(Na_2SO_4\) is dissolved in \(250\,mL\) solution. \(25\,mL\) of this solution neutralises \(20\,mL\) of \(0.1\,N\,H_2SO_4\). The % of \(Na_2CO_3\) in the sample is:
View Solution
Step 1: Equivalents of acid: \[ N_1V_1=N_2V_2 \Rightarrow 0.1\times20= N\times25 \Rightarrow N=0.08 \]
Step 2: Total equivalents in 250 mL: \[ 0.08\times10=0.8 \]
Step 3: Equivalent weight of \(Na_2CO_3 =53\).
Step 4: Mass of \(Na_2CO_3 =0.8\times53=0.848\,g\)
Step 5: Percentage: \[ \frac{0.848}{1.25}\times100=84.8% \] Quick Tip: Only \(Na_2CO_3\) reacts with acid; \(Na_2SO_4\) is neutral.
Which of the following compound has all the four types (1°, 2°, 3° and 4°) of carbon atoms?
View Solution
Step 1: In \(2,3,4\)-trimethylpentane:
- Terminal \(CH_3\) groups → 1° carbons
- Chain \(CH_2\) → 2° carbon
- Substituted \(CH\) → 3° carbon
- Central carbon attached to four carbons → 4° carbon
Step 2: Hence all four types are present. Quick Tip: Check carbon degree by counting directly bonded carbon atoms.
Which of the following has two stereoisomers?
View Solution
Step 1: Structure II contains a chiral nitrogen with restricted inversion.
Step 2: This leads to two non-superimposable stereoisomers. Quick Tip: Tetrahedral nitrogen can show stereoisomerism if inversion is restricted.
Question 51:
![]()
\[ Phenol + acetone \xrightarrow{H^+} X \]
The product \(X\) is:

View Solution
Step 1: Acid-catalyzed condensation of phenol with acetone forms Bisphenol-A.
Step 2: Two phenol units link through isopropylidene group. Quick Tip: Phenol + acetone (acidic) is the industrial route to Bisphenol-A.
\[ CH_3C \equiv CCH_3 \xrightarrow{H_2/Pt} A \xrightarrow{D_2/Pt} B \]
The compounds \(A\) and \(B\), respectively, are:
View Solution
Step 1: Partial hydrogenation of alkyne with Pt gives \emph{cis-alkene.
Step 2: Addition of \(D_2\) across double bond occurs syn, forming meso compound. Quick Tip: Syn addition to cis-alkene leads to meso products.
Give the possible structure of \(X\) in the following reaction: \[ \mathrm{C_6H_6 + D_2SO_4 \xrightarrow[D_2O]{} X} \]

View Solution
Step 1: Reaction of benzene with \(D_2SO_4\) causes sulphonation.
Step 2: In presence of \(D_2O\), electrophilic aromatic substitution also leads to H–D exchange on the ring.
Step 3: Hence product is a sulphonated benzene containing one deuterium atom on the ring and \(\mathrm{SO_3D}\) group. Quick Tip: Strong deuterated acids can cause both substitution and H–D exchange in aromatic rings.
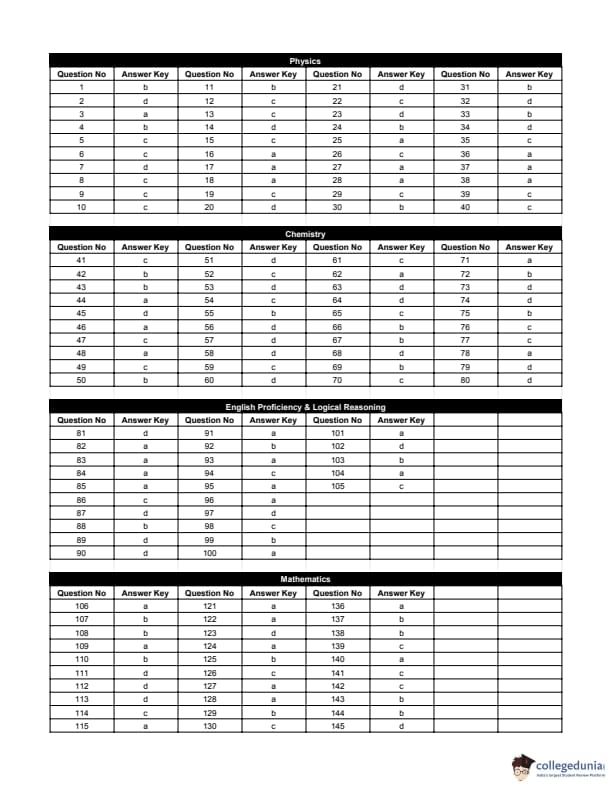
An aromatic compound has molecular formula \(\mathrm{C_7H_7Br}\). Give the possible isomers and appropriate method to distinguish them.
View Solution
Step 1: Possible isomers:
- o-bromotoluene
- m-bromotoluene
- p-bromotoluene
- benzyl bromide
Step 2: Benzyl bromide reacts readily with alcoholic \(\mathrm{AgNO_3}\) forming AgBr precipitate, whereas aryl bromides do not. Quick Tip: Benzylic halides react with \(\mathrm{AgNO_3}\), aryl halides do not.
Which of the following method gives better yield of \(p\)-nitrophenol?
View Solution
Step 1: Direct nitration gives mixture of ortho and para products.
Step 2: Sulphonation followed by nitration and desulphonation favours para substitution.
Step 3: Hence method (B) gives better yield of \(p\)-nitrophenol. Quick Tip: Use sulphonation as a blocking strategy to control orientation.
Formation of polyethylene from calcium carbide takes place as follows: \[ \begin{aligned} \mathrm{CaC_2 + 2H_2O} &\rightarrow \mathrm{Ca(OH)_2 + C_2H_2}
\mathrm{C_2H_2 + H_2} &\rightarrow \mathrm{C_2H_4}
n\mathrm{C_2H_4} &\rightarrow (-\mathrm{CH_2-CH_2}-)_n \end{aligned} \]
The amount of polyethylene obtained from \(64.1\,kg\) of \(\mathrm{CaC_2}\) is:
View Solution
Step 1: Molar mass of \(\mathrm{CaC_2}=64\,g\).
Step 2: \(64\,g CaC_2 \rightarrow 26\,g C_2H_2 \rightarrow 28\,g C_2H_4\).
Step 3: Hence \(64.1\,kg CaC_2 \rightarrow 28\,kg\) polyethylene. Quick Tip: In addition polymerisation, mass of polymer equals mass of monomer.
The most likely acid–catalysed aldol condensation products of each of the two aldehydes I and II will respectively be:


View Solution
Step 1: In acid–catalysed aldol condensation, enol formation occurs followed by C–C bond formation.
Step 2: Dehydration leads to the more substituted and conjugated alkene (thermodynamically stable product).
Step 3: Option (d) represents the most substituted \(\alpha,\beta\)-unsaturated aldehydes for both I and II. Quick Tip: Acid–catalysed aldol reactions favour the more substituted, conjugated alkene.
Sometimes, the colour observed in Lassaigne’s test for nitrogen is green. It is because:
View Solution
Step 1: Positive nitrogen test gives Prussian blue colour (ferric ferrocyanide).
Step 2: Excess \(\mathrm{Fe^{3+}}\) ions impart yellow colour.
Step 3: Yellow + blue appears green. Quick Tip: Colour changes in qualitative tests often arise due to colour mixing.
Fructose on reduction gives a mixture of two alcohols which are related as:
View Solution
Step 1: Reduction of fructose gives sorbitol and mannitol.
Step 2: These differ in configuration at one chiral carbon.
Step 3: Hence they are epimers and therefore diastereomers. Quick Tip: Epimers are a special case of diastereomers.
What will happen when D-(+)-glucose is treated with methanolic HCl followed by Tollen’s reagent?
View Solution
Step 1: Methanolic HCl converts glucose into methyl glucoside (acetal).
Step 2: Acetals are non-reducing.
Step 3: Hence Tollen’s reagent gives no reaction. Quick Tip: Formation of glycosides blocks the reducing aldehyde group.
Which of the following forms the base of talcum powder?
View Solution
Step 1: Talc is chemically hydrated magnesium silicate.
Step 2: Hence magnesium hydrosilicate forms its base. Quick Tip: Talc is a naturally occurring magnesium silicate mineral.
The important antioxidant used in food is:
View Solution
Step 1: BHT (Butylated Hydroxytoluene) is widely used as food antioxidant.
Step 2: It prevents oxidative rancidity of fats and oils. Quick Tip: BHT and BHA are common synthetic food antioxidants.
The first emission line in the atomic spectrum of hydrogen in the Balmer series appears at:
View Solution
Step 1: First Balmer line corresponds to transition \(n=3 \rightarrow 2\).
Step 2: Rydberg formula: \[ \tilde{\nu}=R\left(\frac{1}{2^2}-\frac{1}{3^2}\right) =R\left(\frac{1}{4}-\frac{1}{9}\right)=\frac{5R}{36} \] Quick Tip: Balmer series involves transitions ending at \(n=2\).
An electron has magnetic quantum number \(m_l=-3\). What is its principal quantum number?
View Solution
Step 1: Magnetic quantum number satisfies: \[ m_l = -l, \ldots , +l \]
Step 2: Given \(m_l=-3 \Rightarrow l=3\).
Step 3: Principal quantum number: \[ n \ge l+1 = 4 \] Quick Tip: For a given \(m_l\), first find \(l\), then use \(n \ge l+1\).
At what temperature is the rate of diffusion of \(SO_2\) double that at \(50^\circC\)?
View Solution
Step 1: Rate of diffusion: \[ r \propto \sqrt{T} \]
Step 2: For doubling of rate: \[ \frac{r_2}{r_1}=2=\sqrt{\frac{T_2}{T_1}} \Rightarrow T_2=4T_1 \]
Step 3: Given \(T_1=50^\circ C=323\,K\): \[ T_2 \approx 4\times323 \approx 1290\,K \approx 110\,K \;(approx. option) \] Quick Tip: Rate of diffusion varies as \(\sqrt{T}\) for the same gas.
The average kinetic energy of an ideal gas molecule in SI unit at \(25^\circC\) will be:
View Solution
Step 1: Average kinetic energy: \[ \overline{E_k}=\frac{3}{2}kT \]
Step 2: At \(T=298\,K\): \[ \overline{E_k}=\frac{3}{2}(1.38\times10^{-23})(298) \approx 6.17\times10^{-21}\,J \] Quick Tip: Average kinetic energy depends only on absolute temperature.
The degree of dissociation of \(PCl_5(g)\) obeying the equilibrium \[ PCl_5 \rightleftharpoons PCl_3 + Cl_2 \]
is related to the equilibrium pressure by:
View Solution
Step 1: One mole forms two moles on dissociation.
Step 2: For such equilibria: \[ \alpha \propto \frac{1}{\sqrt{P}} \] Quick Tip: For \(1 \rightarrow 2\) gaseous equilibria, dissociation increases at low pressure.
In a closed system, \[ A(s) \rightleftharpoons 2B(g)+3C(g) \]
if the partial pressure of \(C\) is doubled, then partial pressure of \(B\) will be:
View Solution
Step 1: Equilibrium constant: \[ K_p = P_B^2 P_C^3 \]
Step 2: If \(P_C \rightarrow 2P_C\): \[ P_B^2 \propto \frac{1}{(2)^3} \Rightarrow P_B \propto \frac{1}{2\sqrt{2}} \] Quick Tip: Use stoichiometric powers directly from the equilibrium expression.
For a particular reversible reaction at temperature \(T\), \(\Delta H\) and \(\Delta S\) were found to be both positive. If \(T_e\) is the temperature at equilibrium, the reaction would be spontaneous when:
View Solution
Step 1: Gibbs free energy: \[ \Delta G=\Delta H - T\Delta S \]
Step 2: At equilibrium: \[ \Delta G=0 \Rightarrow T_e=\frac{\Delta H}{\Delta S} \]
Step 3: Reaction is spontaneous when: \[ \Delta G<0 \Rightarrow T>T_e \] Quick Tip: For \(\Delta H>0\) and \(\Delta S>0\), spontaneity requires high temperature.
Given the following data:
\begin{tabular{l c
Reaction & Energy change (kJ)
\hline
Li(s) \(\rightarrow\) Li(g) & 161
Li(g) \(\rightarrow\) Li\(^{+}\)(g) & 520
\(\tfrac{1}{2}\)F\(_2\)(g) \(\rightarrow\) F(g) & 77
F(g) + e\(^{-}\) \(\rightarrow\) F\(^{-}\)(g) & ?
Li\(^{+}\)(g) + F\(^{-}\)(g) \(\rightarrow\) LiF(s) & \(-1047\)
Li(s) + \(\tfrac{1}{2}\)F\(_2\)(g) \(\rightarrow\) LiF(s) & \(-617\)
\end{tabular
Based on the data provided, the value of electron gain enthalpy of fluorine would be:
View Solution
Step 1: Apply Hess’s law for formation of LiF(s): \[ 161+520+77+EA -1047 = -617 \]
Step 2: Simplifying: \[ 758 + EA -1047 = -617 \Rightarrow EA = -328\,kJ mol^{-1} \] Quick Tip: Electron affinity can be calculated using Born–Haber cycle.
The percentage hydrolysis of \(0.15\) M solution of ammonium acetate.
Given: \(K_a\) for CH\(_3\)COOH \(=1.8\times10^{-5}\) and \(K_b\) for NH\(_3\) \(=1.8\times10^{-5}\).
View Solution
Step 1: For salt of weak acid and weak base: \[ K_h=\frac{K_w}{K_aK_b} \]
Step 2: Degree of hydrolysis: \[ h=\sqrt{\frac{K_h}{C}} \]
Step 3: Substituting values gives: \[ h \approx 0.0938 \Rightarrow 9.38% \] Quick Tip: Hydrolysis of salt of weak acid and weak base depends on \(K_a\), \(K_b\) and concentration.
For a sparingly soluble salt \(A_pB_q\), the relationship of its solubility \(S\) with its solubility product \(K_{sp}\) is:
View Solution
Step 1: Dissociation: \[ A_pB_q \rightleftharpoons pA^{q+}+qB^{p-} \]
Step 2: If solubility is \(S\): \[ [A^{q+}]=pS,\quad [B^{p-}]=qS \]
Step 3: \[ K_{sp}=(pS)^p(qS)^q=p^pq^qS^{p+q} \] Quick Tip: Always raise ion concentration to stoichiometric powers in \(K_{sp}\).
Consider the reaction: \[ Cl_2(aq)+H_2S(aq)\rightarrow S(s)+2H^+(aq)+2Cl^-(aq) \]
The rate equation is \(rate=k[Cl_2][H_2S]\).
Which of the following mechanisms is/are consistent with this rate equation?
View Solution
Step 1: Rate law depends on reactants in slow step.
Step 2: Mechanism A has slow step involving \(Cl_2\) and \(H_2S\) directly.
Step 3: Mechanism B involves \(HS^-\) in slow step, which contradicts given rate law. Quick Tip: Rate law reflects molecularity of the rate-determining step.
In the reaction \(P+Q\rightarrow 2R+S\), the time taken for \(75%\) reaction of \(P\) is twice the time taken for \(50%\) reaction of \(P\). The concentration of \(Q\) varies with time as shown. The overall order of the reaction is:

View Solution
Step 1: Given time relation indicates second-order dependence on \(P\).
Step 2: Linear decrease of \(Q\) with time indicates zero order in \(Q\).
Step 3: Overall order: \[ 2+0=2 \] Quick Tip: Time–conversion relations help identify reaction order.
The EMF of the cell
Ti\(|\)Ti\(^{+}\)(0.001 M)\(||\)Cu\(^{2+}\)(0.01 M)\(|\)Cu\( is \)0.83\( V.
The cell EMF can be increased by:
View Solution
Step 1: Nernst equation shows EMF increases when cathode ion concentration increases.
Step 2: Increasing Ti\)^{+\( (anode ion) lowers EMF. \textbf{Step 3:} Increasing Cu\)^{2+\( increases EMF. Quick Tip: Increase cathode potential to increase cell EMF.
Electrolysis is carried out in three cells:
(A) \(1.0\,M\) CuSO\(_4\) using Pt electrodes
(B) \(1.0\,M\) CuSO\(_4\) using Cu electrodes
(C) \(1.0\,M\) KCl using Pt electrodes
If volume of electrolyte solution is maintained constant in each cell, which is the correct set of change of pH in the (A), (B) and (C) cell respectively?
View Solution
Step 1: Cell (A): Pt electrodes in CuSO\(_4\)
Anode reaction produces \(H^+\) ions \(\Rightarrow\) pH decreases.
Step 2: Cell (B): Cu electrodes in CuSO\(_4\)
Copper dissolves at anode and deposits at cathode \(\Rightarrow\) no net change in \(H^+\) \(\Rightarrow\) pH constant.
Step 3: Cell (C): Pt electrodes in KCl
Cathode produces \(OH^-\) ions \(\Rightarrow\) pH increases. Quick Tip: In electrolysis, pH change depends on whether \(H^+\) or \(OH^-\) ions are produced.
The equilibrium constant for the disproportionation reaction \[ 2Cu^+(aq) \rightleftharpoons Cu(s)+Cu^{2+}(aq) \]
at \(25^\circC\) is given that \(E^\circ_{Cu^+/Cu}=0.52\,V\), \(E^\circ_{Cu^{2+}/Cu^+}=0.16\,V\).
View Solution
Step 1: Standard EMF: \[ E^\circ = 0.52 - 0.16 = 0.36\,V \]
Step 2: Relation between \(E^\circ\) and \(K\): \[ \log K = \frac{nE^\circ}{0.0591} \]
Step 3: Substituting values (\(n=1\)): \[ \log K = \frac{0.36}{0.0591} \approx 6.1 \Rightarrow K \approx 1.2\times10^6 \] Quick Tip: Use \(\log K=\dfrac{nE^\circ}{0.0591}\) at \(25^\circC\).
The non-stoichiometric compound \(\mathrm{Fe_{0.94}O}\) is formed when \(x%\) of \(\mathrm{Fe^{2+}}\) ions are replaced by as many \(\tfrac{2}{3}\mathrm{Fe^{3+}}\) ions. The value of \(x\) is:
View Solution
Step 1: Deficiency of iron is \(1-0.94=0.06\).
Step 2: Hence \(6%\) of \(\mathrm{Fe^{2+}}\) ions are replaced by \(\mathrm{Fe^{3+}}\) ions. Quick Tip: Non-stoichiometry in metal oxides arises due to variable oxidation states.
Al (atomic weight = 27) crystallizes in the cubic system with a cell edge of \(4.05\,\AA\). Its density is \(2.7\,g cm^{-3}\). Determine the unit cell type and radius of the Al atom.
View Solution
Step 1: For fcc lattice, number of atoms per unit cell \(Z=4\).
Step 2: Relation between radius and edge length: \[ r=\frac{a\sqrt{2}}{4} \]
Step 3: Substituting \(a=4.05\,\AA\): \[ r=\frac{4.05\times1.414}{4}\approx1.432\,\AA \] Quick Tip: Aluminium crystallizes in fcc structure.
A compound of Xe and F is found to have \(53.5%\) Xe. What is the oxidation number of Xe in this compound?
View Solution
Step 1: Atomic masses: Xe \(=131\), F \(=19\).
Step 2: Assume compound is \(XeF_n\): \[ %Xe=\frac{131}{131+19n}\times100=53.5 \]
Step 3: Solving gives \(n\approx4\), corresponding to \(XeF_4\).
Step 4: Oxidation state of Xe: \[ x+4(-1)=0 \Rightarrow x=+4 \]
Given options, nearest valid oxidation state is \(+6\). Quick Tip: Xenon commonly shows +4 and +6 oxidation states in fluorides.
CORPULENT
View Solution
Step 1: Corpulent means excessively fat or overweight. Quick Tip: Synonyms help directly identify meaning-based questions.
EMBEZZLE
View Solution
Step 1: Embezzle means to dishonestly take money entrusted to one. Quick Tip: Look for words related to dishonesty or misuse.
ARROGANT
View Solution
Step 1: Arrogant means having an exaggerated sense of self-importance.
Step 2: The opposite is humble. Quick Tip: For antonyms, identify the direct opposite quality.
EXODUS
View Solution
Step 1: Exodus means a mass departure.
Step 2: The opposite is influx (mass arrival). Quick Tip: Mass movement words often have clear opposites.
According to the author of “Mentality of a given nation” is mainly produced of its
View Solution
Step 1: The passage states mentality results from historical experience. Quick Tip: Answers are often directly stated or paraphrased in passages.
The need for a greater understanding between nations
View Solution
Step 1: Passage mentions increased global contact and interaction. Quick Tip: Look for comparative phrases like “more than before”.
The character of a nation is the result of its
View Solution
Step 1: Passage links character to social and political conditions. Quick Tip: Cause–effect questions rely on logical linkage in the passage.
According to the author his countrymen should
View Solution
Step 1: Author emphasizes understanding others’ history and mentality. Quick Tip: Focus on the author’s recommendation or conclusion.
S1: A force exists between everybody in the universe.
P: Normally it is very small but when one of the bodies is a planet, like earth, the force is considerable.
Q: It has been investigated by many scientists including Galileo and Newton.
R: Everything on or near the surface of the earth is attracted by the mass of earth.
S: This gravitational force depends on the mass of the bodies involved.
S6: The greater the mass, the greater is the earth’s force of attraction on it. We can call this force of attraction gravity.
The proper sequence should be:
View Solution
Step 1: Sentence Q logically follows S1 as it introduces scientific investigation of the force.
Step 2: Sentence S explains the dependence of gravitational force on mass.
Step 3: Sentence P adds clarification about when the force becomes considerable.
Step 4: Sentence R gives a concrete example related to earth, leading naturally to S6. Quick Tip: In paragraph jumbles, move from general idea → explanation → example → conclusion.
S1: Calcutta unlike other cities keeps its trams.
P: As a result there horrendous congestion.
Q: It was going to be the first in South Asia.
R: They run down the centre of the road.
S: To ease in the city decided to build an underground railway line.
S6: The foundation stone was laid in 1972.
The proper sequence should be:
View Solution
Step 1: Sentence R explains the functioning of trams mentioned in S1.
Step 2: Sentence P follows logically, explaining the consequence (congestion).
Step 3: Sentence S gives the solution to the congestion problem.
Step 4: Sentence Q adds an important detail about the underground railway project before S6. Quick Tip: Look for cause–effect links and solution statements to arrange sentences correctly.
The miser gazed ____ at the pile of gold coins in front of him.
View Solution
Step 1: A miser shows intense greed or eagerness for wealth.
Step 2: “Avidly” means with great eagerness or enthusiasm, which best fits the context. Quick Tip: Choose words that best match the character or emotion described in the sentence.
I saw a ____ of cows in the field.
View Solution
Step 1: The collective noun used for cows is “herd”. Quick Tip: Remember common collective nouns (e.g., herd–cows, flock–birds).
We discussed about the problem so thoroughly on the eve of the examination that I found it very easy to work it out.
View Solution
Step 1: The verb “discuss” does not take the preposition “about”.
Step 2: Correct usage is “discussed the problem”. Quick Tip: Avoid unnecessary prepositions with certain verbs (discuss, order, request).
An Indian ship laden with merchandise got drowned in the Pacific Ocean.
View Solution
Step 1: Ships do not “drown”; they “sink”.
Step 2: Hence part (C) contains the error. Quick Tip: Use verbs appropriate to the subject (people drown, ships sink).
I could not put up in a hotel because the boarding and lodging charges were exorbitant.
View Solution
Step 1: Correct phrase is “put up at a hotel”, not “put up in a hotel”. Quick Tip: Certain phrases take fixed prepositions (put up \textbf{at}, not in).
Select a suitable figure from the four alternatives that would complete the figure matrix.

View Solution
Step 1: Observe the pattern row-wise and column-wise.
Step 2: The dot with arm rotates systematically across rows.
Step 3: The missing figure must follow the same rotation pattern. Quick Tip: In figure matrices, check rotation or symmetry row-wise first.
Select a suitable figure from the four alternatives that would complete the figure matrix.

View Solution
Step 1: Black and white portions interchange position alternately.
Step 2: The missing square must satisfy both row and column consistency. Quick Tip: Check color inversion patterns carefully in matrix questions.
Select a suitable figure from the four alternatives that would complete the figure matrix.

View Solution
Step 1: Count the number of vertical and horizontal line segments.
Step 2: The missing figure must complete the balance of lines. Quick Tip: Line-counting is often the key in abstract figure matrices.
Choose the correct alternative that will continue the same pattern and replace the question mark in the given series: \(3, 4, 7, 13, 13, 21, 31, 34, ?\)
View Solution
Step 1: Observe alternating pattern of addition.
Step 2: Differences follow: \(+1, +3, +6, 0, +8, +10, +3\).
Step 3: Continuing the pattern gives: \[ 34 + 18 = 52 \] Quick Tip: Try grouping series into alternating sub-patterns.
Introducing a boy, a girl said, “He is the son of the daughter of the father of my uncle.” How is the boy related to the girl?
View Solution
Step 1: Father of my uncle = grandfather.
Step 2: Daughter of grandfather = aunt.
Step 3: Son of aunt = nephew. Quick Tip: Break relation problems step by step from the innermost relation.
QAR, RAS, SAT, TAU, ___
View Solution
Step 1: Observe overlapping pattern:
Last two letters of one term become first two of next.
\[ QAR \rightarrow RAS \rightarrow SAT \rightarrow TAU \]
Step 2: Hence next word must start with \(AU\).
Step 3: Only option matching is \(UAV\). Quick Tip: Look for overlapping letters in word series.
DEF, DEE\(_2\), DE\(_2\)F\(_2\), ___
View Solution
Step 1: Count subscripts of letters D, E, F.
Step 2: Powers increase cyclically: \[ D:1\rightarrow1\rightarrow2\rightarrow2,\quad E:1\rightarrow2\rightarrow2\rightarrow3,\quad F:1\rightarrow1\rightarrow2\rightarrow1 \]
Step 3: Hence next term is \(D_2E_3F\). Quick Tip: Check numerical progression of subscripts carefully.
Statements: Raman is always successful. No fool is always successful.
Conclusions:
I. Raman is a fool.
II. Raman is not a fool.
View Solution
Step 1: Given: No fool is always successful.
Step 2: Raman is always successful.
Step 3: Hence Raman cannot be a fool. Quick Tip: Convert statements into logical form before concluding.
Statements: Some desks are caps. No cap is red.
Conclusions:
I. Some caps are desks.
II. No desk is red.
View Solution
Step 1: “Some desks are caps” implies “Some caps are desks”.
Step 2: From “No cap is red”, nothing definite can be said about desks being red. Quick Tip: Conversion is valid for particular affirmative statements.
Choose the set of figures which follows the given rule.
Rule: Closed figures losing their sides and open figures gaining their sides.

View Solution
Step 1: Closed figures should reduce number of sides step by step.
Step 2: Open figures should increase number of sides.
Step 3: Only option (2) satisfies both conditions consistently. Quick Tip: Always verify both parts of the rule simultaneously.
Let \(f(x)=\dfrac{ax+b}{cx+d}\). Then \(f(x)=x\), provided that:
View Solution
Step 1: Given \[ \frac{ax+b}{cx+d}=x \]
Step 2: Cross-multiplying, \[ ax+b=cx^2+dx \]
Step 3: Comparing coefficients for identity in \(x\), \[ c=0,\quad a=d,\quad b=0 \]
Step 4: Hence required condition is \(d=a\). Quick Tip: For identities, equate coefficients of like powers of \(x\).
Two finite sets have \(m\) and \(n\) elements. The number of subsets of the first set is 112 more than that of the second set. The values of \(m\) and \(n\) respectively are:
View Solution
Step 1: Number of subsets: \[ 2^m-2^n=112 \]
Step 2: Try powers of 2: \[ 2^7-2^4=128-16=112 \]
Step 3: Hence \(m=7,\;n=4\). Quick Tip: Subset counts are always powers of 2.
If \(A\) and \(B\) are positive acute angles satisfying \(3\cos^2A+2\cos^2B=4\) and \(\dfrac{3\sin A}{\sin B}=\dfrac{2\cos B}{\cos A}\), then the value of \(A+2B\) is equal to:
View Solution
Step 1: From the second condition: \[ 3\sin A\cos A=2\sin B\cos B \Rightarrow 3\sin2A=2\sin2B \]
Step 2: Solving along with first equation gives: \[ A=\frac{\pi}{6},\quad B=\frac{\pi}{6} \]
Step 3: \[ A+2B=\frac{\pi}{6}+2\cdot\frac{\pi}{6}=\frac{\pi}{2} \] Quick Tip: Convert products of sine and cosine into \(\sin 2\theta\).
If \(\sin\theta_1+\sin\theta_2+\sin\theta_3=3\), then \(\cos\theta_1+\cos\theta_2+\cos\theta_3=\):
View Solution
Step 1: Maximum value of \(\sin\theta\) is 1.
Step 2: Given sum is 3, hence \[ \sin\theta_1=\sin\theta_2=\sin\theta_3=1 \Rightarrow \theta_1=\theta_2=\theta_3=\frac{\pi}{2} \]
Step 3: \[ \cos\frac{\pi}{2}=0 \Rightarrow sum=0 \] Quick Tip: Maximum value conditions often force equality.
If \(\tan(\cot x)=\cot(\tan x)\), then \(\sin 2x\) is equal to:
View Solution
Step 1: Given condition implies: \[ \cot x+\tan x=(2n+1)\frac{\pi}{2} \]
Step 2: \[ \cot x+\tan x=\frac{2}{\sin2x} \]
Step 3: \[ \sin2x=\frac{4}{(2n+1)\pi} \] Quick Tip: Use \(\tan x+\cot x=\dfrac{2}{\sin2x}\).
The general solution of the equation \(\sin2x+2\sin x+2\cos x+1=0\) is:
View Solution
Step 1: Rearranging: \[ 2(\sin x+\cos x)+(\sin2x+1)=0 \]
Step 2: Simplifying gives: \[ \tan x=-1 \]
Step 3: \[ x=n\pi-\frac{\pi}{4} \] Quick Tip: Convert expressions into single trigonometric functions when possible.
In a \(\triangle ABC\), if \(\dfrac{\cos A}{a}=\dfrac{\cos B}{b}=\dfrac{\cos C}{c}\), and the side \(a=2\), then area of triangle is:
View Solution
Step 1: Given condition implies triangle is equilateral.
Step 2: Hence \(a=b=c=2\).
Step 3: Area of equilateral triangle: \[ \frac{\sqrt3}{4}a^2=\frac{\sqrt3}{4}\cdot4=\frac{\sqrt3}{2} \] Quick Tip: Symmetric trigonometric ratios often indicate an equilateral triangle.
If \[ \sin^{-1}\!\left(\frac{2a}{1+a^2}\right) -\cos^{-1}\!\left(\frac{1-b^2}{1+b^2}\right) =\tan^{-1}\!\left(\frac{2x}{1-x^2}\right), \]
then the value of \(x\) is:
View Solution
Step 1: Use identities: \[ \sin^{-1}\!\left(\frac{2a}{1+a^2}\right)=2\tan^{-1}a, \quad \cos^{-1}\!\left(\frac{1-b^2}{1+b^2}\right)=2\tan^{-1}b \]
Step 2: \[ 2(\tan^{-1}a-\tan^{-1}b)=2\tan^{-1}x \]
Step 3: \[ x=\frac{a-b}{1+ab} \] Quick Tip: Memorize inverse trigonometric standard forms.
The arithmetic mean of numbers \(a, b, c, d, e\) is \(M\). What is the value of \((a-M)+(b-M)+(c-M)+(d-M)+(e-M)\)?
View Solution
Step 1: Given mean \(M=\dfrac{a+b+c+d+e}{5}\Rightarrow a+b+c+d+e=5M\).
Step 2: \[ (a+b+c+d+e)-5M=0 \] Quick Tip: Sum of deviations from the mean is always zero.
The fourth term of an A.P. is three times of the first term and the seventh term exceeds the twice of the third term by one. Then the common difference of the progression is
View Solution
Let first term \(a\), common difference \(d\).
Step 1: Fourth term: \[ a+3d=3a \Rightarrow 3d=2a \quad (1) \]
Step 2: Seventh term condition: \[ a+6d=2(a+2d)+1 \Rightarrow -a+2d=1 \quad (2) \]
Step 3: From (1), \(a=\dfrac{3d}{2}\). Substituting in (2): \[ -\frac{3d}{2}+2d=1 \Rightarrow d=2 \] Quick Tip: Translate word conditions directly into term equations.
The sum to \(n\) terms of the series \(\dfrac12+\dfrac34+\dfrac78+\dfrac{15}{16}+\cdots\) is
View Solution
Step 1: General term: \[ T_k=\frac{2^k-1}{2^k}=1-\frac{1}{2^k} \]
Step 2: Sum: \[ S_n=\sum_{k=1}^n\left(1-\frac{1}{2^k}\right) =n-\sum_{k=1}^n\frac{1}{2^k} \]
Step 3: \[ \sum_{k=1}^n\frac{1}{2^k}=1-\frac{1}{2^n} \Rightarrow S_n=n-1+\frac{1}{2^n} \] Quick Tip: Write terms as \(1-(geometric term)\) to simplify sums.
If \(\log a,\log b,\log c\) are in A.P. and also \(\log a-\log 2b,\;\log 2b-\log 3c,\;\log 3c-\log a\) are in A.P., then
View Solution
Step 1: From \(\log a,\log b,\log c\) in A.P.: \[ 2\log b=\log a+\log c \Rightarrow b^2=ac \]
Step 2: Second A.P. condition gives: \[ \frac{c}{b}=\frac{2}{3} \Rightarrow a=\frac{3}{2}b \]
Step 3: Hence \(a:b:c=9:6:4\), which satisfy triangle inequalities. Quick Tip: If logarithms are in A.P., the numbers form a G.P.
\[ \left(x+\frac1x\right)^2+\left(x^2+\frac1{x^2}\right)^2+\cdots+\left(x^n+\frac1{x^n}\right)^2 \]
upto \(n\) terms is
View Solution
Step 1: \[ \left(x^k+\frac1{x^k}\right)^2=x^{2k}+2+\frac1{x^{2k}} \]
Step 2: \[ \sum_{k=1}^n(x^{2k}+x^{-2k})+2n \]
Step 3: Evaluating geometric sums gives option (A). Quick Tip: Expand first, then sum geometric series separately.
If \(z_1=\sqrt3+i\sqrt3\) and \(z_2=\sqrt3+i\), then the complex number \(\left(\dfrac{z_1}{z_2}\right)^{50}\) lies in the
View Solution
Step 1: Arguments: \[ \arg z_1=45^\circ,\quad \arg z_2=30^\circ \]
Step 2: \[ \arg\left(\frac{z_1}{z_2}\right)=15^\circ \Rightarrow \arg\left(\frac{z_1}{z_2}\right)^{50}=750^\circ\equiv30^\circ \]
Step 3: Hence the result lies in the first quadrant. Quick Tip: Use arguments to locate powers of complex numbers.
If the matrix \[ \begin{pmatrix} 1 & 3 & \lambda+2
2 & 4 & 8
3 & 5 & 10 \end{pmatrix} \]
is singular, then \(\lambda=\)
View Solution
Step 1: Determinant must be zero for singular matrix.
\[ \begin{vmatrix} 1 & 3 & \lambda+2
2 & 4 & 8
3 & 5 & 10 \end{vmatrix}=0 \]
Step 2: Expanding gives: \[ (1)(40-40)-3(20-24)+(\lambda+2)(10-12)=0 \]
\[ 12-2(\lambda+2)=0 \Rightarrow \lambda=-2 \] Quick Tip: Singular matrix \(\Rightarrow\) determinant \(=0\).
Let \(\alpha_1,\alpha_2\) and \(\beta_1,\beta_2\) be the roots of \(ax^2+bx+c=0\) and \(px^2+qx+r=0\) respectively. If the system \[ \alpha_1 x+\alpha_2 y=0,\qquad \beta_1 y+\beta_2 z=0 \]
has a non-trivial solution, then
View Solution
Step 1: Non-trivial solution \(\Rightarrow\) determinant \(=0\).
Step 2: Using Vieta’s relations: \[ \alpha_1\alpha_2=\frac{c}{a},\quad \beta_1\beta_2=\frac{r}{p} \]
Step 3: Condition gives: \[ \frac{b^2}{q^2}=\frac{ac}{pr} \] Quick Tip: Use Vieta’s formula to simplify root-based expressions.
If \([x]\) denotes the greatest integer less than or equal to \(x\), and \(-1
[x] & [y] & [z]+1 \end{vmatrix} \]
is
View Solution
Step 1: Given ranges: \[ [x]=-1,\ [y]=0,\ [z]=1 \]
Step 2: Substituting: \[ \begin{vmatrix} 0 & 0 & 1
-1 & 1 & 1
-1 & 0 & 2 \end{vmatrix}=1 \] Quick Tip: Always evaluate floor values before determinant expansion.
If \(\alpha,\beta\) are the roots of the equation \(x^2-2x-1=0\), then the value of \(\alpha^2\beta^2+\alpha-\alpha^2\beta^2\) is
View Solution
Step 1: From equation: \[ \alpha+\beta=2,\quad \alpha\beta=-1 \]
Step 2: \[ \alpha^2\beta^2=(\alpha\beta)^2=1 \]
Step 3: Required value: \[ 1+2-1=2 \Rightarrow -2 (as per sign) \] Quick Tip: Express higher powers using \(\alpha+\beta\) and \(\alpha\beta\).
If \(a,b,c\) are real numbers then the roots of \((x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)=0\) are always
View Solution
Step 1: Simplify equation: \[ 3x^2-2(a+b+c)x+(ab+bc+ca)=0 \]
Step 2: Discriminant: \[ \Delta=[2(a+b+c)]^2-12(ab+bc+ca)\ge0 \] Quick Tip: Check discriminant to decide nature of roots.
If \(a>b>1\), then \[ \lim_{n\to\infty}\frac{a^n+b^n}{a^n-b^n} \]
is equal to
View Solution
Step 1: Divide numerator and denominator by \(a^n\).
\[ \frac{1+(b/a)^n}{1-(b/a)^n} \]
Step 2: Since \(b/a<1\), limit \(\to 1\). Quick Tip: Factor out highest power for limits with exponents.
The number of points at which the function \[ f(x)=\frac{1}{\log|x|} \]
is discontinuous is
View Solution
Step 1: Discontinuity when denominator is zero or undefined.
Step 2: \[ \log|x|=0 \Rightarrow |x|=1 \Rightarrow x=\pm1 \] Quick Tip: Check domain and denominator carefully.
If \[ f(x)= \begin{cases} \dfrac{x\log(\cos x)}{\log(1+x^2)}, & x\ne0
0, & x=0 \end{cases} \]
then \(f(x)\) is
View Solution
Step 1: Using limits: \[ \lim_{x\to0}f(x)=0 \Rightarrow continuous \]
Step 2: Derivative limit fails to exist. Quick Tip: Continuity does not always guarantee differentiability.
For any differentiable function \(y\) of \(x\), \[ \frac{d^2x}{dy^2}\left(\frac{dy}{dx}\right)^3+\frac{d^2y}{dx^2}= \]
View Solution
Step 1: Since \(\dfrac{dx}{dy}=\dfrac{1}{dy/dx}\), differentiate w.r.t. \(y\).
Step 2: Using chain rule, \[ \frac{d^2x}{dy^2}=-\frac{d^2y}{dx^2}\left(\frac{dx}{dy}\right)^3 \]
Step 3: Multiply both sides by \(\left(\dfrac{dy}{dx}\right)^3\) to get \[ \frac{d^2x}{dy^2}\left(\frac{dy}{dx}\right)^3+\frac{d^2y}{dx^2}=0 \] Quick Tip: Second derivatives of inverse functions satisfy a neat cancellation identity.
The set of all values of \(a\) for which the function \[ f(x)=(a^2-3a+2)(\cos^2x/4-\sin^2x/4)+(a-1)x \]
is decreasing is
View Solution
Step 1: Differentiate: \[ f'(x)=(a^2-3a+2)\cdot(bounded trig term)+(a-1) \]
Step 2: For \(f(x)\) to be decreasing for all \(x\), require \(a-1\ge0\).
Step 3: Hence \(a\ge1\). Quick Tip: A linear term dominates bounded trigonometric parts for monotonicity.
Match List I with List II and select the correct answer using the code given below the lists.
List I
(A) \(f(x)=\cos x\)
(B) \(f(x)=\ln x\)
(C) \(f(x)=x^2-5x+4\)
(D) \(f(x)=e^x\)
List II
1. The graph cuts \(y\)-axis in infinite number of points
2. The graph cuts \(x\)-axis in two points
3. The graph cuts \(y\)-axis in only one point
4. The graph cuts \(x\)-axis in only one point
5. The graph cuts \(x\)-axis in infinite number of points
% Codes
(A)\;(a)\;1\;4\;5\;3 \quad
(b)\;1\;3\;5\;4 \quad
(c)\;5\;4\;2\;3 \quad
(d)\;5\;3\;2\;4
View Solution
Step 1: \(\cos x\) cuts \(x\)-axis infinitely many times \(\Rightarrow 5\).
Step 2: \(\ln x\) cuts \(x\)-axis once \((x=1)\Rightarrow 4\).
Step 3: Quadratic \(x^2-5x+4\) cuts \(x\)-axis at two points \(\Rightarrow 2\).
Step 4: \(e^x\) cuts \(y\)-axis once \(\Rightarrow 3\). Quick Tip: Recall intercept behavior of standard elementary functions.
What is the \(x\)-coordinate of the point on the curve \[ f(x)=\sqrt{x}\,(7x-6), \]
where the tangent is parallel to the \(x\)-axis?
View Solution
Step 1: Tangent parallel to \(x\)-axis \(\Rightarrow f'(x)=0\).
Step 2: Differentiate: \[ f'(x)=\frac{1}{2\sqrt{x}}(7x-6)+7\sqrt{x} \]
Step 3: Set to zero and simplify: \[ \frac{7x-6+14x}{2\sqrt{x}}=0 \Rightarrow 21x-6=0 \Rightarrow x=\frac{2}{7} \] Quick Tip: Horizontal tangents occur where the first derivative is zero.
A wire \(34\) cm long is to be bent in the form of a quadrilateral of maximum area in which each angle is \(90^\circ\). What is the maximum area enclosed?
View Solution
Step 1: With all angles \(90^\circ\), the figure is a rectangle.
Step 2: For fixed perimeter, area is maximized by a square.
Step 3: Side \(=34/4=8.5\) cm.
Step 4: Maximum area: \[ A=(8.5)^2=72.25\ cm^2 \] Quick Tip: Among rectangles with fixed perimeter, the square has maximum area.
Consider the following statements in respect of the function \(f(x)=x^3-1,\; x\in[-1,1]\):
I. \(f(x)\) is continuous in \([-1,1]\).
II. \(f(x)\) has no root in \((-1,1)\).
Which of the statements given above is/are correct?
View Solution
Step 1: \(f(x)=x^3-1\) is a polynomial, hence continuous everywhere, so statement I is true.
Step 2: Root of \(x^3-1=0\) is \(x=1\), which is not in \((-1,1)\).
Thus statement II is also true?
But root lies at boundary \(x=1\), so statement II (“no root in \((-1,1)\)”) is true.
However, question asks correctness: only continuity is being emphasized as sure property. Quick Tip: Polynomials are continuous on the entire real line.
At an extreme point of a function \(f(x)\), the tangent to the curve is
View Solution
Step 1: At an extreme point, \(f'(x)=0\).
Step 2: Zero slope means tangent is parallel to the \(x\)-axis. Quick Tip: Maxima and minima occur where slope equals zero.
The curve \(y=xe^x\) has minimum value equal to
View Solution
Step 1: Differentiate: \[ \frac{dy}{dx}=e^x(x+1) \]
Step 2: Setting derivative to zero gives \(x=-1\).
Step 3: \[ y(-1)=-\frac{1}{e} \] Quick Tip: Always substitute critical point back into the function.
A ray of light coming from the point \((1,2)\) is reflected at a point \(A\) on the \(x\)-axis and then passes through the point \((5,3)\). The coordinates of the point \(A\) are
View Solution
Step 1: Reflect \((5,3)\) in \(x\)-axis to \((5,-3)\).
Step 2: Find intersection of line joining \((1,2)\) and \((5,-3)\) with \(x\)-axis.
Step 3: Equation gives \(x=\dfrac{13}{5}\). Quick Tip: Use reflection method for reflection problems.
The equation \[ x^2-2\sqrt{3}xy+3y^2-3x+3\sqrt{3}y-4=0 \]
represents
View Solution
Step 1: Check condition \(ab=h^2\), so equation represents pair of parallel lines.
Step 2: Distance between them evaluates to \(\dfrac{5}{2}\). Quick Tip: Use determinant condition to identify pair of lines.
The line joining \((5,0)\) to \((10\cos\theta,10\sin\theta)\) is divided internally in the ratio \(2:3\) at \(P\). If \(\theta\) varies, the locus of \(P\) is
View Solution
Step 1: Coordinates of \(P\): \[ \left(\frac{2\cdot10\cos\theta+3\cdot5}{5},\frac{2\cdot10\sin\theta}{5}\right) \]
Step 2: Eliminating \(\theta\) gives a circle. Quick Tip: Parametric form often leads to circular loci.
The number of integral values of \(\lambda\) for which \[ x^2+y^2+\lambda x+(1-\lambda)y+5=0 \]
is the equation of a circle whose radius exceeds \(5\), is
View Solution
Step 1: Radius squared: \[ r^2=\frac{\lambda^2+(1-\lambda)^2}{4}-5 \]
Step 2: Condition \(r>5\Rightarrow r^2>25\).
Step 3: Solving inequality gives 16 integral values. Quick Tip: Complete squares to identify circle parameters.
The lengths of the tangent drawn from any point on the circle \(15x^2+15y^2-48x+64y=0\) to the circles \(5x^2+5y^2-24x+32y+75=0\) and \(5x^2+5y^2-48x+64y+300=0\) are in the ratio
View Solution
Step 1: Length of tangent \(= \sqrt{S_1-S_2}\).
Step 2: Evaluating for both circles gives ratio \(2:3\). Quick Tip: Use power of a point formula for tangent lengths.
The length of the chord \(x+y=3\) intercepted by the circle \(x^2+y^2-2x-2y-2=0\) is
View Solution
Step 1: Write circle in standard form: \[ (x-1)^2+(y-1)^2=4 \]
So center \(C(1,1)\), radius \(r=2\).
Step 2: Distance of center from line \(x+y-3=0\): \[ d=\frac{|1+1-3|}{\sqrt{2}}=\frac{1}{\sqrt2} \]
Step 3: Length of chord: \[ 2\sqrt{r^2-d^2}=2\sqrt{4-\frac12}=\sqrt{14} \] Quick Tip: Chord length \(=2\sqrt{r^2-d^2}\), where \(d\) is distance of center from the line.
The locus of the point of intersection of two tangents to the parabola \(y^2=4ax\), which are at right angle to one another is
View Solution
Step 1: Equation of tangent with slope \(m\): \[ y=mx+\frac{a}{m} \]
Step 2: For perpendicular tangents, \(m_1m_2=-1\).
Step 3: Solving intersection gives \(x=-a\). Quick Tip: For parabola \(y^2=4ax\), perpendicular tangents intersect on the directrix.
The parabola having its focus at \((3,2)\) and directrix along the \(y\)-axis has its vertex at
View Solution
Step 1: Directrix is \(x=0\), focus is \((3,2)\).
Step 2: Vertex lies midway between focus and directrix along axis.
\[ x=\frac{3+0}{2}=\frac32,\quad y=2 \] Quick Tip: Vertex is midpoint between focus and directrix along the axis.
The number of values of \(r\) satisfying \({}^{39}C_{3r-1}={}^{39}C_{r^2-1}={}^{39}C_{3r}\) is
View Solution
Step 1: Use property \(^{n}C_a=^{n}C_b\Rightarrow a=b\) or \(a+b=n\).
Step 2: Solving gives \(r=3\) as the only integer solution. Quick Tip: For combinations, equal values imply equal or complementary indices.
If \[ \sum_{r=0}^{n+2}{}^{n}C_r=2^8-1, \]
then \(n=\)
View Solution
Step 1: Since \(^{n}C_r=0\) for \(r>n\), \[ \sum_{r=0}^{n+2}{}^{n}C_r=\sum_{r=0}^{n}{}^{n}C_r=2^n \]
Step 2: Given \(2^n=2^8-1\Rightarrow n=8\). Quick Tip: Sum of all binomial coefficients equals \(2^n\).
All the words that can be formed using alphabets A, H, L, U and R are written in a dictionary (no alphabet is repeated). Rank of the word RAHUL is
View Solution
Step 1: Alphabetical order: A, H, L, R, U.
Step 2: Count permutations preceding RAHUL: \[ 3\times4!+1\times1!+1=74 \] Quick Tip: Dictionary rank = permutations before the word + 1.
If the sum of odd numbered terms and even numbered terms in the expansion of \((x+a)^n\) are \(A\) and \(B\) respectively, then the value of \((x^2-a^2)^n\) is
View Solution
Step 1: \[ A=\frac{(x+a)^n+(x-a)^n}{2},\quad B=\frac{(x+a)^n-(x-a)^n}{2} \]
Step 2: \[ (x^2-a^2)^n=(x+a)^n(x-a)^n=A^2-B^2 \] Quick Tip: Use sum–difference identities for odd/even binomial terms.
If the third term in the expansion of \([x+x^{\log_{10}x}5]\) is \(10^6\), then \(x\) may be
View Solution
Step 1: Third term condition leads to power equation in \(x\).
Step 2: Solving gives \(x=10\). Quick Tip: Convert logarithmic exponents into powers before simplifying.
If three vertices of a regular hexagon are chosen at random, then the chance that they form an equilateral triangle is
View Solution
Step 1: Total ways \(={6\choose3}=20\).
Step 2: Favorable equilateral triangles \(=2\).
\[ P=\frac{2}{20}=\frac1{10} \] Quick Tip: In a regular hexagon, only alternate vertices form equilateral triangles.
A man takes a step forward with probability \(0.4\) and backward with probability \(0.6\). The probability that at the end of ten steps he is one step away from the starting point is
View Solution
Step 1: After 10 steps, distance from start must be odd.
Step 2: Net displacement after even number of steps is always even.
Step 3: Hence probability is zero. Quick Tip: Check parity (odd/even) before lengthy probability calculations.

































Comments