GATE 2022 Engineering Sciences (XE) Question Paper Available - Download Here with Solution PDF

The movie was funny and I _____ .

• (A) could help laughing
• (B) couldn't help laughed
• (C) couldn't help laughing
• (D) could helped laughed

If \( x : y : z = \frac{1}{2} : \frac{1}{3} : \frac{1}{4} \), what is the value of \( \frac{x + z - y}{y} \)?

• (A) 0.75
• (B) 1.25
• (C) 2.25
• (D) 3.25

Both the numerator and the denominator of \( \frac{3}{4} \) are increased by a positive integer, \( x \), and those of \( \frac{15}{17} \) are decreased by the same integer. This operation results in the same value for both the fractions. What is the value of \( x \)?

• (A) 1
• (B) 2
• (C) 3
• (D) 4

A survey of 450 students about their subjects of interest resulted in the following outcome.
150 students are interested in Mathematics.
200 students are interested in Physics.
175 students are interested in Chemistry.
50 students are interested in Mathematics and Physics.
60 students are interested in Physics and Chemistry.
40 students are interested in Mathematics and Chemistry.
30 students are interested in Mathematics, Physics and Chemistry.
Remaining students are interested in Humanities.
Based on the above information, the number of students interested in Humanities is:

• (A) 10
• (B) 30
• (C) 40
• (D) 45

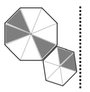
For the picture shown above, which one of the following is the correct picture representing reflection with respect to the mirror shown as the dotted line?

In the last few years, several new shopping malls were opened in the city. The total number of visitors in the malls is impressive. However, the total revenue generated through sales in the shops in these malls is generally low. Which one of the following is the CORRECT logical inference based on the information in the above passage?

• (A) Fewer people are visiting the malls but spending more
• (B) More people are visiting the malls but not spending enough
• (C) More people are visiting the malls and spending more
• (D) Fewer people are visiting the malls and not spending enough

In a partnership business, the monthly investment by three friends for the first six months is in the ratio 3: 4: 5. After six months, they had to increase their monthly investments by 10%, 15%, and 20%, respectively, of their initial monthly investment. The new investment ratio was kept constant for the next six months. What is the ratio of their shares in the total profit (in the same order) at the end of the year such that the share is proportional to their individual total investment over the year?

• (A) 22 : 23 : 24
• (B) 22 : 33 : 50
• (C) 33 : 46 : 60
• (D) 63 : 86 : 110

Consider the following equations of straight lines:
Line L1: \( 2x - 3y = 5 \)
Line L2: \( 3x + 2y = 8 \)
Line L3: \( 4x - 6y = 5 \)
Line L4: \( 6x - 9y = 6 \)
Which one among the following is the correct statement?

• (A) L1 is parallel to L2 and L1 is perpendicular to L3
• (B) L2 is parallel to L4 and L2 is perpendicular to L1
• (C) L3 is perpendicular to L4 and L3 is parallel to L2
• (D) L4 is perpendicular to L2 and L4 is parallel to L3

Given below are two statements and four conclusions drawn based on the statements.
Statement 1: Some soaps are clean.
Statement 2: All clean objects are wet.
Conclusion I: Some clean objects are soaps.
Conclusion II: No clean object is a soap.
Conclusion III: Some wet objects are soaps.
Conclusion IV: All wet objects are soaps.
Which one of the following options can be logically inferred?

• (A) Only conclusion I is correct
• (B) Either conclusion I or conclusion II is correct
• (C) Either conclusion III or conclusion IV is correct
• (D) Only conclusion I and conclusion III are correct

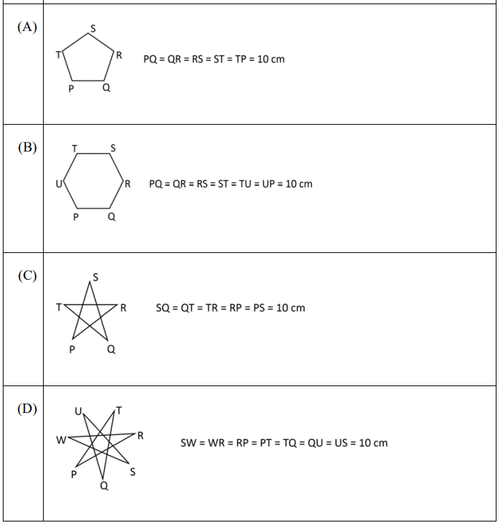
An ant walks in a straight line on a plane leaving behind a trace of its movement. The initial position of the ant is at point P facing east.
The ant first turns 72º anticlockwise at P, and then does the following two steps in sequence exactly FIVE times before halting.
1. Moves forward by 10 cm.
2. Turns 144º clockwise.
The pattern made by the trace left behind by the ant is:

The value of \[ \lim_{x \to 0} \frac{1}{x} \int_{2}^{2+x} \left(t + \sqrt{t^2 + 5}\right) dt \]

• (A) 0
• (B) 4
• (C) 5
• (D) 6

Let \( \mathbb{C} = \{ z = x + iy : x and y are real numbers, i = \sqrt{-1} \} \) be the set of complex numbers. Let the function \( f(z) = u(x, y) + i v(x, y) \) for \( z = x + iy \in \mathbb{C} \) be analytic in \( \mathbb{C} \), where \[ u(x, y) = x^3 y - y x^3 \quad and \quad v(x, y) = \frac{x^4}{4} + \frac{y^4}{4} - \frac{3}{2} x^2 y^2. \]
If \( f'(z) \) denotes the derivative of \( f(z) \), then:

• (A) \( |f'(1 + i)|^2 = 1 \)
• (B) \( |f'(-1 + i)|^2 = 7 \)
• (C) \( |f'(-1 + i)|^2 = 8 \)
• (D) \( |f'(1 + i)|^2 = 10 \)

If the partial differential equation \[ (x + 2) \frac{\partial^2 u}{\partial x^2} + 2(x + y) \frac{\partial^2 u}{\partial x \partial y} + 2(y - 1) \frac{\partial^2 u}{\partial y^2} - 3y^2 \frac{\partial u}{\partial y} = 0 \]
is parabolic on the circle \( (x - a)^2 + (y - b)^2 = r^2 \), then the values of \( a \), \( b \), and \( r \) are given by:

• (A) \( a = 1, b = 2, r = 1 \)
• (B) \( a = -1, b = 2, r = 1 \)
• (C) \( a = 1, b = -2, r = 1 \)
• (D) \( a = -1, b = -2, r = 1 \)

Let \( \Gamma \) be the positively oriented circle \( x^2 + y^2 = 9 \) in the xy-plane. If \[ \oint_{\Gamma} (3y + e^x \sin x) \, dx + \left( 7x + \sqrt{e^y + 2} \right) \, dy = \alpha \pi, \]
where \( \alpha \) is a real constant, then \( \alpha \) is equal to ________.

Let \( y_1(x) \) and \( y_2(x) \) be two linearly independent solutions of the differential equation: \[ x^2 \frac{d^2y}{dx^2} - 2x \frac{dy}{dx} + 2y = 0, \quad x > 0. \]
Let \( W(y_1, y_2)(x) \) denote the Wronskian of \( y_1(x) \) and \( y_2(x) \) at \( x \).
If \( W(y_1, y_2)(1) = 1 \), then \( W(y_1, y_2)(2) \) is equal to ________.

Let \[ A = \begin{pmatrix} 2 & 0 & 1
1 & 2 & 5
0 & 3 & 0
0 & 0 & 1 \end{pmatrix} \]
. Then the sum of the geometric multiplicities of the distinct eigenvalues of \( A \) is equal to ________.

In a cosmopolitan city, the population comprises of 30% female and 70% male. Suppose that 5% of females and 30% of males in the population are foreigners. A person is selected at random from this population. Given that the selected person is a foreigner, the probability that the person is a female is ________ (round off to three decimal places).

• (A) \( 2 + \log 2 \)
• (B) \( 2 - \log 2 \)
• (C) \( 2 + \log 4 \)
• (D) \( 2 - \log 4 \)
• (A) both P and Q are TRUE
• (B) P is TRUE and Q is FALSE
• (C) P is FALSE and Q is TRUE
• (D) both P and Q are FALSE

Let \( f : \mathbb{R}^2 \to \mathbb{R} \) be given by \[ f(x, y) = 4xy - 2x^2 - y^4 + 1. \]
The number of critical points where \( f \) has local maximum is equal to ________.

If the quadrature rule \[ \int_{-1}^1 f(x) \, dx \approx f(\alpha) + \gamma f(\beta), \]
where \( \alpha, \beta \) and \( \gamma \) are real constants, is exact for all polynomials of degree \( \leq 3 \), then \( \gamma + 3 (\alpha^2 + \beta^2) + (\alpha^3 + \beta^3) \) is equal to ________.

• (A) \( \frac{\pi D^2}{4} \rho g \)
• (B) \( \frac{\pi D^2}{8} \rho g \)
• (C) \( \frac{\pi D^2}{2} \rho g \)
• (D) \( \frac{\pi D^2}{3} \rho g \)
• (A) \( \tau_A > \tau_B \)
• (B) \( \tau_B > \tau_A \)
• (C) \( \tau_C > \tau_B \)
• (D) \( \tau_C > \tau_D \)

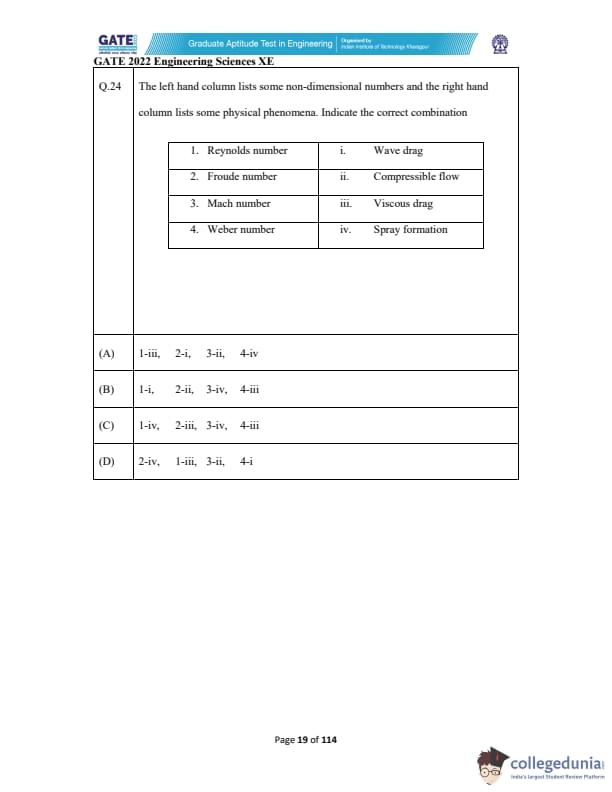
The left-hand column lists some non-dimensional numbers and the right-hand column lists some physical phenomena. Indicate the correct combination.

• (A) 1-iii, 2-i, 3-ii, 4-iv
• (B) 1-i, 2-ii, 3-iv, 4-iii
• (C) 1-iv, 2-iii, 3-iv, 4-iii
• (D) 2-iv, 1-iii, 3-ii, 4-i

As temperature increases:

• (A) The dynamic viscosity of a gas increases.
• (B) The dynamic viscosity of a liquid decreases.
• (C) The dynamic viscosity of a liquid does not change.
• (D) The dynamic viscosity of a gas decreases.

Which of the following statement(s) regarding a venturimeter is/are correct?

• (A) In the direction of flow, it consists of a converging section, a throat, and a diverging section.
• (B) In the direction of flow, it consists of a diverging section, a throat, and a converging section.
• (C) It is used for flow measurement at a very low Reynolds number.
• (D) Pressure tappings are provided just upstream of the venturimeter and at the throat.

Which of the following statement(s) is/are true for streamlines in a steady incompressible flow?

• (A) Two streamlines cannot intersect each other.
• (B) Flow rate increases between two diverging streamlines.
• (C) Flow rate decreases between two diverging streamlines.
• (D) Stream function has a constant value along a streamline.

A flow has a velocity potential given by \( \phi = Ax^3 \) where ‘A’ is a non-zero constant. Which of the following statement(s) is/are true about the flow?

• (A) The flow is incompressible.
• (B) The flow is irrotational.
• (C) The flow has local acceleration.
• (D) The flow has convective acceleration.

A boundary layer develops due to a two-dimensional steady flow over a horizontal flat plate. Consider a vertical line away from the leading edge which extends from the wall to the edge of the boundary layer. Which of the following quantity/quantities is/are not constant along the vertical line? \( u \) and \( v \) represent the components of velocity in the direction along the plate and normal to it, respectively, and \( x \) is taken along the length of the plate while \( p \) is the pressure.

• (A) \( u \)
• (B) \( \frac{\partial u}{\partial x} \)
• (C) \( v \)
• (D) \( p \)

A 10 kg mass placed on an infinitely long horizontal massless flat platform is to be supported by a steady vertical water jet as shown in the figure. The diameter of the jet is 5 cm. What minimum average velocity is required to hold the mass in place?

Consider an inviscid flow through a smooth pipe which has a pitot-static tube arrangement as shown. Find the centre-line velocity in the pipe. Consider that the density of the fluid is 1000 kg/m\(^3\), acceleration due to gravity is 10 m/s\(^2\), and the specific gravity of the manometric fluid is 11.

• (A) 2 m/s
• (B) 3 m/s
• (C) 5 m/s
• (D) 7 m/s

The speed of propagation, \(c\), of a capillary wave depends on the density of the fluid, \(\rho\), the wavelength of the wave, \(\lambda\), and the surface tension, \(\sigma\). The dimensions are: \(\rho = ML^{-3}\), \(\lambda = L\), and \(\sigma = MT^{-2}\). Which expression is dimensionally correct?

• (A) \(c = \sqrt{\frac{\sigma}{\rho \lambda}}\)
• (B) \(c = \sqrt{\frac{\sigma}{\rho \lambda^2}}\)
• (C) \(c = \sqrt{\frac{\rho}{\sigma \lambda}}\)
• (D) \(c = \sqrt{\frac{\lambda}{\rho \sigma}}\)

A two-dimensional flow field is described by a combination of a source of strength \( m \) at the origin and a uniform flow \( U \) in the positive x-direction such that the velocity potential is given by \[ \phi = Ux + \frac{m}{2\pi} \ln \sqrt{x^2 + y^2} \]
The stagnation streamline is shown in the figure. Find the distance \( aa' \).

• (A) \( \frac{m}{U} \)
• (B) \( \frac{2m}{U} \)
• (C) \( \frac{8m}{U} \)
• (D) \( \frac{m}{2U} \)

A typical boundary layer over a flat plate has a linear velocity profile with zero velocity at the wall and freestream velocity \(U_{\infty}\) at the outer edge of the boundary layer. What is the ratio of the momentum thickness to the thickness of the boundary layer?

• (A) \( \frac{1}{2} \)
• (B) \( \frac{1}{4} \)
• (C) \( \frac{1}{6} \)
• (D) \( \frac{1}{3} \)

Identify the configuration(s) in which steady two-dimensional internal flow may show boundary layer separation if the flow direction is left to right.

Consider steady fully developed flow of a liquid through two large horizontal flat parallel plates separated by a distance of 2 mm. One of the plates is fixed and the other plate moves at a speed of 0.5 m/s. What is the magnitude of the pressure gradient (in Pa/m) in the direction of the flow required to ensure that the net flow through the plates is zero?

Dynamic viscosity of the liquid is \(5 \times 10^{-4}\) Ns/m\(^2\)

(Round off to the nearest integer)

Consider two-dimensional turbulent flow of air over a horizontal flat plate of length 1 m. Skin friction coefficient at a length \(x\) from the leading edge is given by:
\[ c_f = \frac{0.06}{(Re_x)^{0.2}} \]

where \(Re_x\) is the local Reynolds number. Find the drag force per unit width (in N/m\(^2\)) on the plate if the free stream velocity is 10 m/s. Density and dynamic viscosity of air are 1.2 kg/m\(^3\) and \(1.83 \times 10^{-5}\) Ns/m\(^2\).

(Round off to three decimal places)

For an inviscid fluid with density \( \rho = 1 \, kg/m^3 \), the Cartesian velocity field is: \[ \mathbf{u} = (-2x + y)\mathbf{i} + (2x + y)\mathbf{j} \, m/s \]
Neglecting body forces, find the magnitude of the pressure gradient (Pa/m) at \((x,y) = (1\,m, 1\,m)\) at \( t = 1\,s \).
(Round off to two decimal places)

A lawn sprinkler has horizontal arms of radius \( a = 10\,cm = 0.1\,m \).
Water exits through jets of area \( A = 25\,cm^2 = 2.5\times10^{-3}\,m^2 \) with velocity \( V = 1\,m/s \).
Each jet leaves orthogonal to the arm and makes a \( 60^\circ \) angle with the horizontal.
Find the torque (N·m) required to hold the sprinkler stationary.
(Round off to two decimal places).

A wooden cylinder (specific gravity = 0.6) of length \(L\) and diameter \(D\) floats in water (density 1000 kg/m\(^3\)). Find out the minimum value of \(D/L\) for which the cylinder floats with its axis vertical.

(Round off to three decimal places)

A cart of mass 10 kg is placed on a \(60^\circ\) inclined plane. A turning vane (weight negligible) is mounted on the cart. A horizontal water jet from a 0.1 m\(^2\) nozzle strikes the vane and is turned downward parallel to the inclined plane. Find the minimum jet velocity (m/s) so that the cart does not slide down. Neglect friction. Water density = 1000 kg/m\(^3\), \(g = 10\) m/s\(^2\).

(Round off to two decimal places)

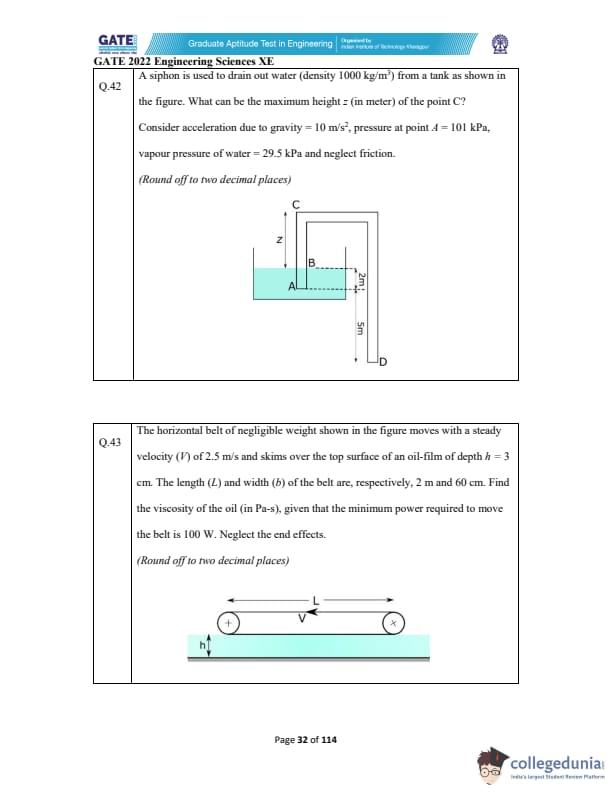
A siphon is used to drain water (density \(1000\,kg/m^3\) ) from a tank as shown.
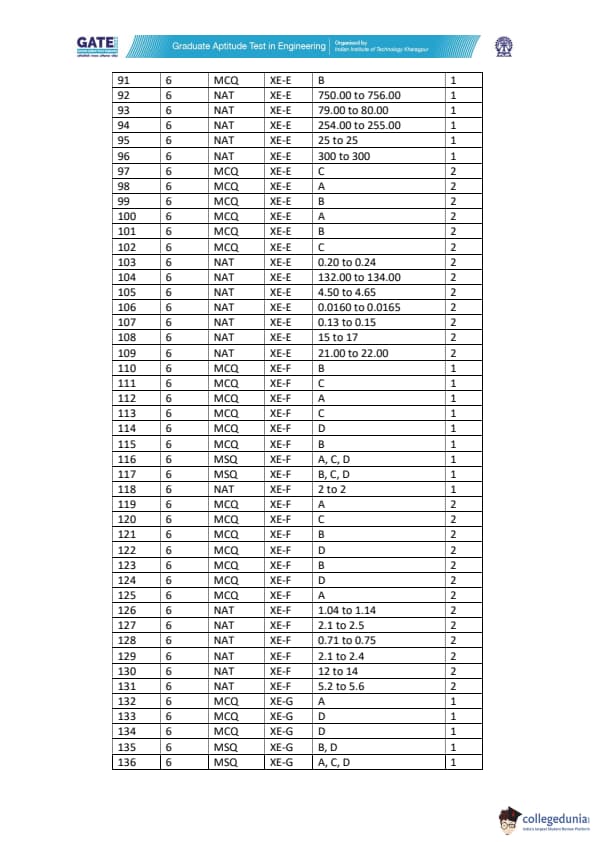
What is the maximum height \(z\) (in meters) of point C?
Take g = 10\,\text{m/s^2,\; p_A = 101\,\text{kPa,\; \text{vapour pressure = 29.5\,\text{kPa,\; \text{and neglect friction.
(Round off to two decimal places)

A horizontal belt of negligible weight moves with velocity \(V = 2.5\,m/s\)
over an oil film of depth \(h = 3\,cm = 0.03\,m\).
The belt has length \(L = 2\,m\) and width \( b = 0.6\,m \).
Find the viscosity of the oil (Pa·s) if minimum power required is 100 W.
Neglect end effects.
(Round off to two decimal places)

Number of atoms per unit area of the (110) plane of a body centered cubic crystal, with lattice parameter \(a\), is

• (A) \(\frac{1}{a^2}\)
• (B) \(\frac{\sqrt{2}}{a^2}\)
• (C) \(\frac{1}{\sqrt{3}\, a^2}\)
• (D) \(\frac{1}{\sqrt{2}\, a^2}\)

Match the following materials with their corresponding bonding types.

• (A) P - 4;\; Q - 2;\; R - 3;\; S - 1
• (B) P - 3;\; Q - 4;\; R - 2;\; S - 1
• (C) P - 3;\; Q - 2;\; R - 1;\; S - 4
• (D) P - 3;\; Q - 1;\; R - 4;\; S - 2

In an ideal rubber, the primary factor responsible for elasticity up to small strains is

• (A) Change in both enthalpy and entropy
• (B) Change in enthalpy, but no change in the entropy
• (C) No change in enthalpy, but change in the entropy
• (D) Neither a change in enthalpy, nor a change in the entropy

Which one of the following statements is true for an intrinsic semiconductor?

• (A) Electrical conductivity increases with increasing temperature and pressure
• (B) Electrical conductivity increases with increasing temperature and decreasing pressure
• (C) Electrical conductivity increases with decreasing temperature and increasing pressure
• (D) Electrical conductivity increases with decreasing temperature and pressure

A differential scanning calorimetry (DSC) experiment tracks the heat flow into or out of a system as a function of temperature. If the experiments given in the options below are performed at 1 atmospheric pressure, then in which case will the DSC thermogram exhibit a spike, either upward or downward?

• (A) Heating 10 mg of pure Cu from 323 K to 673 K
• (B) Cooling pure water from 323 K to 278 K
• (C) Heating pure ice from 263 K to 284 K
• (D) Cooling a Pb-Sn alloy at the eutectic composition from 323 K to 273 K

Which one of the following solvent environments will likely result in swelling of solid polystyrene?

• (A) 0.1 M NaOH in H\textsubscript{2}O
• (B) HCl (aq.) of pH = 6
• (C) Distilled water
• (D) Benzene

Vickers microhardness (HV) of a ductile material A is higher than another ductile material B. Which of the following is/are true?

• (A) Young’s modulus of A is greater than B
• (B) Yield strength of A is greater than B
• (C) Scratch resistance of A is greater than B
• (D) Ductility of A is greater than B

The enthalpy required to create an oxygen vacancy in CeO\(_2\) is 4 eV. The number of oxygen vacancies present per mole of CeO\(_2\) at 1000 K is _________.

(Round off to the nearest integer)


Given: \(N_A = 6.02 \times 10^{23}\) mole\(^{-1}\) \(k_B = 8.62 \times 10^{-5}\) eV/K

An electrochemical reaction is known to occur at +4.50 V against a Li\(^+\)/Li reference electrode. The potential of the same reaction against a Zn\(^{2+}\)/Zn reference electrode is _________.

(Round off to two decimal places)


Given standard electrode potentials:
Li\(^+\)/Li : \(E^\circ = -3.04\) V
Zn\(^{2+}\)/Zn : \(E^\circ = -0.76\) V

For a binary system at constant pressure, there are two types of invariant reactions:

(i) \( \alpha \leftrightarrow \beta + \gamma \)

(ii) \( \alpha + \beta \leftrightarrow \gamma \)

Analogously, how many different types of invariant reactions may exist under variable temperature and pressure, for a binary system?

• (A) 1
• (B) 2
• (C) 3
• (D) 4

For a glass marginally below its glass transition temperature, which one of the following statements is true?

• (A) Glass has higher enthalpy than both the corresponding crystalline and liquid phases
• (B) Glass has lower enthalpy than both the corresponding crystalline and liquid phases
• (C) Glass has higher entropy than the corresponding crystalline phase and lower entropy than the corresponding liquid phase
• (D) Glass has lower entropy than the corresponding crystalline phase and higher entropy than the corresponding liquid phase

Which one of the following samples of high-purity aluminium (Al) single crystal will plastically yield at the lowest applied load under ambient conditions? Loading axis is along the direction shown in the schematic.

• (A) (i)
• (B) (ii)
• (C) (iii)
• (D) (iv)

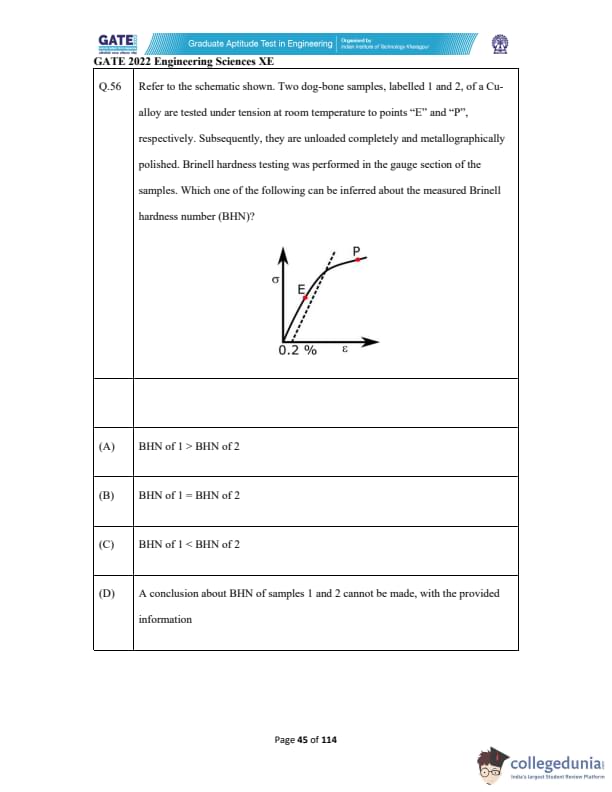
Refer to the schematic shown. Two dog-bone samples, labelled 1 and 2, of a Cu-alloy are tested under tension at room temperature to points “E” and “P”, respectively. Subsequently, they are unloaded completely and metallographically polished. Brinell hardness testing was performed in the gauge section of the samples. Which one of the following can be inferred about the measured Brinell hardness number (BHN)?

• (A) BHN of 1 \(>\) BHN of 2
• (B) BHN of 1 = BHN of 2
• (C) BHN of 1 \(<\) BHN of 2
• (D) A conclusion about BHN of samples 1 and 2 cannot be made, with the provided information

During the ageing of a homogenized Al-Cu alloy (1 to 4 wt.% Cu) below the GP zone solvus, hardness of the alloy:

• (A) increases monotonically
• (B) decreases monotonically
• (C) first increases and then decreases
• (D) first decreases and then increases

A student aims to deposit a thin metallic film on SiO\(_2\) substrate, with an adhesion layer between the metal film and substrate, in a contiguous planar fashion. Island type of growth must be avoided. The student performs an extensive optimization exercise. Which one of the following steps is in the right direction?

• (A) Choose a metallic adhesion layer with very low interfacial energy with the deposited thin film
• (B) Choose a metallic adhesion layer with very low interfacial energy with SiO\(_2\), irrespective of its interaction with metal film to be deposited
• (C) Increase the substrate temperature and decrease the deposition rate
• (D) Use intermittent stages of deposition followed by annealing

For a diffusional transformation (i.e., growth of \( \beta \) precipitates in an \( \alpha \) matrix), which of the following is/are true with increasing degree of undercooling?

• (A) Rate of transformation first increases and then decreases
• (B) Rate of transformation first decreases and then increases
• (C) Thermodynamic driving force increases monotonically
• (D) Mobility of atoms in \( \alpha \) matrix remains unchanged

A two-phase (\(\alpha + \beta\)) mixture of an A–B binary system has the following properties:


[(i)] Phase \(\alpha\) has equal weight percentages of A and B.
[(ii)] Phase \(\beta\) has twice the mole fraction of A compared to B.
[(iii)] The two-phase mixture has equal amounts of \(\alpha\) and \(\beta\).
[(iv)] Atomic mass of A is twice that of B.


The mole fraction of A in the resultant two-phase mixture is _________.

(Round off to one decimal)

Component A diffuses into a solid to a depth of 10 μm in 1 hour at 300 K.
Treat diffusion in one dimension.
Find the time (in seconds) for A to diffuse to the same depth at 600 K.
(Round off to 1 decimal).


Diffusivity is given by: \[ D_A = D_A^0 \exp\left( -\frac{E_a}{k_B T} \right) \]

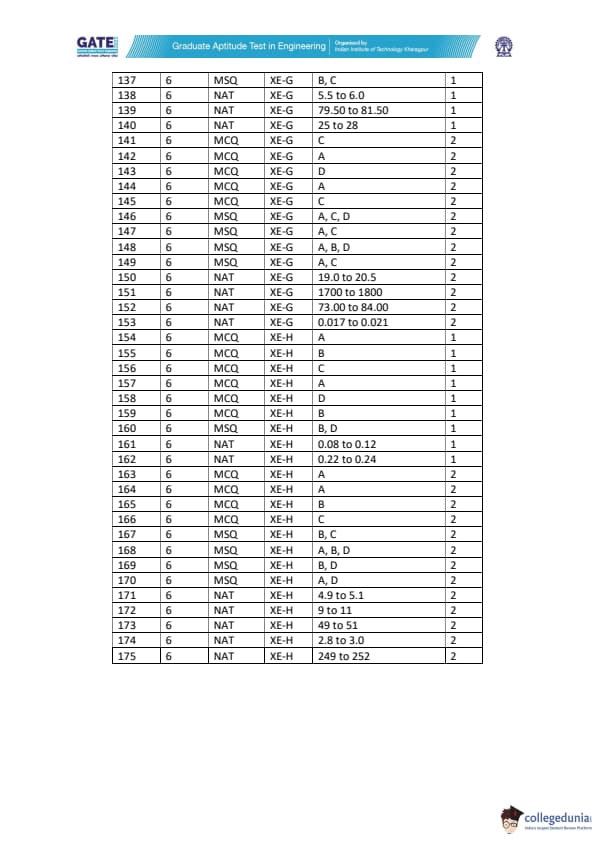
Given: \[ E_a = 0.3 eV, \quad k_B = 8.62\times10^{-5}\,eV/K \]
Depth is same → use relation: \[ x \sim \sqrt{Dt} \Rightarrow Dt = constant \]
Thus: \[ \frac{t_2}{t_1} = \frac{D_1}{D_2} \]

A spherical \(\beta\) particle nucleates from the \(\alpha\) matrix on a non-deformable substrate \(\delta\), forming a contact angle \(\theta\) as shown. The value of \(\dfrac{\Delta G^{}_{het}}{\Delta G^{}_{hom}}\) is _________.

(Round off to three decimal places)




Given:
\(\alpha\)–\(\beta\) interfacial energy \(= 0.4\) J/m\(^{2}\) \(\alpha\)–\(\delta\) interfacial energy \(= 0.3\) J/m\(^{2}\) \(\beta\)–\(\delta\) interfacial energy \(= 0.02\) J/m\(^{2}\)

The resistivity of a pure semiconductor at 298 K is \(3000\,\Omegam\).
Assume the number of electrons excited \((n_e)\) across the band gap is \[ n_e = N_A \exp\left(-\frac{E_g}{k_B T}\right) \]
Given: \[ N_A = 6.02 \times 10^{23}\ mol^{-1},\quad k_B = 8.62 \times 10^{-5}\ eV/K,\quad T = 298\ K \]
Mobilities: \[ \mu_e = 0.14\ m^2/(V·s),\quad \mu_h = 0.06\ m^2/(V·s) \]
Absolute electron charge: \[ q = 1.60 \times 10^{-19}\ C \]

A new glass material is developed to minimize the transmission of light through a window with a glass panel of thickness 5 mm. The refractive index of the glass material is 1.5 and the absorption coefficient can be changed from 0.3 cm\(^{-1}\) to 1 cm\(^{-1}\). In the given range of absorption coefficients, the ratio of the maximum to the minimum fraction of the light coming out of the other side of the glass panel is _________.

(Round off to two decimal places)

The third peak in the X-ray diffraction pattern of a face-centered cubic (FCC) crystal occurs at a \(2\theta = 45^\circ\).
The wavelength of the monochromatic X-ray beam is \(1.54\ \AA\).
Considering first-order reflection, find the lattice parameter (in \AA).
(Round off to two decimal places)

A force \( F \) is applied at an angle \( \theta = 30^\circ \) on an elastic column as shown in the figure. \(E\) and \(I\) are respectively the Young's modulus and the area moment of inertia. The smallest magnitude of \(F\) needed to cause buckling is:

• (A) \( \dfrac{2\pi^2 EI}{\sqrt{3}\,L^2} \)
• (B) \( \dfrac{\sqrt{3}\,\pi^2 EI}{2L^2} \)
• (C) \( \dfrac{\pi^2 EI}{2L^2} \)
• (D) \( \dfrac{2\pi^2 EI}{L^2} \)

The shear stress due to a transverse shear force in a linear elastic isotropic beam of rectangular cross-section

• (A) varies linearly along the depth in the transverse direction of the beam
• (B) is zero at the neutral axis
• (C) is maximum at the neutral axis
• (D) remains constant along the depth in the transverse direction of the beam

A massless semicircular rod held fixed at end A is in the xy-plane as shown. A force P along the negative z direction is acting at point B on the rod. The unit vectors along x, y and z directions are denoted by i, j and k. Due to the applied force P, the cross-section of the rod at point D will be subjected to

• (A) a twisting moment \(PR(1-\cos\theta)\,\mathbf{i}\), a bending moment \(PR\sin\theta\,\mathbf{j}\), and a shear force \(-P\,\mathbf{k}\)
• (B) a twisting moment \(PR(1-\sin\theta)\,\mathbf{i}\), a bending moment \(PR\cos\theta\,\mathbf{j}\), and a shear force \(P\,\mathbf{k}\)
• (C) a twisting moment \(PR(\cos\theta-1)\,\mathbf{i}\), a bending moment \(-PR\sin\theta\,\mathbf{j}\), and a shear force \(-P\,\mathbf{k}\)
• (D) a twisting moment \(PR\sin\theta\,\mathbf{i}\), a bending moment \(PR(1-\cos\theta)\,\mathbf{j}\), and a shear force \(P\,\mathbf{k}\)

In the truss shown in the figure, all the members are pin jointed to each other. The members AB, BD, DE and DC have the same length. For the given loading, which of the following is the correct statement?

• (A) BD is a zero-force member, and AB and ED are in compression
• (B) AB is in tension, ED is in compression, and BD is a zero-force member
• (C) AB and DC are in tension, and BC is in compression
• (D) ED is in tension, and DC and BC are in compression

End B of the 2 m long rigid rod \(AB\) is constrained to move horizontally in the slot as shown in the figure and has a velocity of \(1.0\,\mathbf{i}\) m/s. The angular velocity of the rod at the instant shown is \(2\) rad/s. The unit vectors along \(x\) and \(y\) directions are denoted by \(\mathbf{i}\) and \(\mathbf{j}\). The velocity of point A in m/s is then given by:

• (A) \((1 - 2\sqrt{3})\mathbf{i} + 2\mathbf{j}\)
• (B) \((1 + 2\sqrt{3})\mathbf{i} - 2\mathbf{j}\)
• (C) \(-2\sqrt{3}\mathbf{i} + 2\mathbf{j}\)
• (D) \(2\sqrt{3}\mathbf{i} - 2\mathbf{j}\)

The assembly of four masses connected by rigid mass-less rods is kept on a smooth horizontal floor as shown in the figure. Under the applied force \(2F\), the magnitude of angular acceleration of the assembly at the instant shown is:

• (A) \(\dfrac{F}{mc}\)
• (B) \(\dfrac{F}{2mc}\)
• (C) \(\dfrac{2F}{3mc}\)
• (D) \(\dfrac{F}{3mc}\)

A particle is constrained to move at a constant speed on an inclined plane (ABCD) along the curved path shown in the figure. Edges AD and BC are parallel to the y-axis. The inclined plane makes an angle \(\theta\) with the \(xy\)-plane. The velocity vector of the particle makes an angle \(\phi\) with the dotted line which is parallel to edge AB. If the speed of the particle is 2 m/s, \(\phi = 30^\circ\), and \(\theta = 40^\circ\), then the z-component of the velocity of the particle in m/s is

• (A) \(-1.32\)
• (B) \(-1.00\)
• (C) \(-1.11\)
• (D) \(-1.50\)

A uniform elastic rod of constant cross-section is fixed at its left end as shown. An axial force \(P\) acts as shown. Assume plane sections remain plane. The ratio of axial displacement at point \(A\) \((x=4L)\) to that at point \(B\) \((x=L)\) is _________ (rounded off to one decimal place).

A thin-walled spherical pressure vessel has radius 500 mm and thickness 10 mm. Yield strength is 500 MPa. The internal pressure at which yielding occurs according to Tresca criterion is _________ MPa (rounded off to one decimal place).

The beam in the figure is subjected to a moment \( M_0 \) at mid span as shown. Which of the following is the vertical reaction at B?

• (A) \( \dfrac{9M_0}{8L} \)
• (B) \( \dfrac{15M_0}{8L} \)
• (C) \( \dfrac{3M_0}{4L} \)
• (D) \( \dfrac{9M_0}{4L} \)

A spring–mass system having a mass \(m\) and spring constant \(k\), placed horizontally on a foundation, is connected to a vertically hanging mass \(m\) with the help of an inextensible string as shown. Ignore pulley friction, and neglect pulley, string, and spring inertia. Gravity acts downward. The natural frequency of the system in rad/s is:

• (A) \(\sqrt{\dfrac{4k}{3m}}\)
• (B) \(\sqrt{\dfrac{k}{2m}}\)
• (C) \(\sqrt{\dfrac{k}{3m}}\)
• (D) \(\sqrt{\dfrac{4k}{5m}}\)

One end of a uniform rigid rod \(OA\) of length \(L\) and mass \(m\) is attached to a frictionless hinge at \(O\). The other end of the rod is connected to the roof at \(B\) with a massless inextensible thread \(AB\). Initially the rod is horizontal and at rest. The gravity is acting vertically downward as shown. Immediately after the thread \(AB\) is cut, the reaction on the rod at \(O\) is:

• (A) \(\dfrac{mg}{4}\) in the positive \(y\)-direction
• (B) \(\dfrac{mg}{2}\) in the negative \(y\)-direction
• (C) \(\dfrac{3mg}{4}\) in the negative \(y\)-direction
• (D) \(mg\) in the positive \(y\)-direction

A circular shaft is rigidly connected to a wall at one end. The shaft has a solid portion and a hollow portion as shown in the figure. The length of each portion is \(L\) and the shear modulus of the material is \(G\). The polar moment of inertia of the hollow portion is \(J\) and that of the solid portion is \(50J\). A torque \(T\) is applied at the rightmost end as shown. The rotation of the section \(PQ\) is

• (A) \(\displaystyle \frac{27TL}{100JG}\)
• (B) \(\displaystyle \frac{TL}{40JG}\)
• (C) \(\displaystyle \frac{5TL}{4JG}\)
• (D) \(\displaystyle \frac{3TL}{4JG}\)

A rectangular plate of uniform thickness having initial length \( a \) and width \( b \) is placed between two rigid immovable walls. The temperature of the plate is increased by \( \Delta T \). The plate is free to expand along the \( y \) and \( z \) directions. The mid-surface of the plate remains in the \( xy \)-plane. The Poisson’s ratio is \( \nu \) and the coefficient of thermal expansion is \( \alpha \). Assuming that the plate is initially free of stresses, the change in length of the plate after the increase in temperature is given by:

• (A) \( a(1-\nu)\alpha\Delta T \)
• (B) \( a(1+\nu)\alpha\Delta T \)
• (C) \( a\alpha\Delta T \)
• (D) \( 2a\alpha\Delta T \)

A mass \( m = 10 \, kg \) is attached to a spring as shown in the figure. The coefficient of friction between the mass and the inclined plane is 0.25. Assume that the acceleration due to gravity is \( 10 \, m/s^2 \) and that static and kinetic friction coefficients are the same. Equilibrium of the mass is impossible if the spring force is:

• (A) 30 N
• (B) 45 N
• (C) 60 N
• (D) 75 N

The frame shown is subjected to a uniformly distributed load of 1000 N/m over 0.6 m. Neglecting the frame weight, the maximum shear force (in N) in the region between supports A and B is _________.

A slider moves in a frictionless slot and is connected via a spring OA. Given: spring stiffness = 2 kN/m, mass = 10 kg, unstretched spring length = 1 m. If released from rest at A, find velocity (m/s) when passing through B.

(Rounded to nearest integer)

A sphere A of mass \(m\) is thrown at 50 m/s along \(\tan^{-1}(3/4)\).
At the topmost point of its trajectory, it collides centrally with sphere B (mass \(3m\)) at rest.
Gravity g = 10\,\text{m/s^2. Coefficient of restitution e = 0.3.
Find the speed (m/s) of sphere A immediately after collision (round to 1 decimal).

A truck moves at 20 m/s carrying a 1000 kg box.
Coefficient of friction between box and platform is \(\mu = 0.25\).
Find the shortest stopping distance so that the box does not slip.
(round off to nearest integer).

A stepped rod of length 2 m is fixed at both ends A and C. The area of cross-section of AB is 200 mm\(^{2}\) and that of BC is 100 mm\(^{2}\). A force \(F\) is applied at section B causing a displacement of 0.1 mm in the direction of the force. Young’s modulus of the rod is 200 GPa. The applied force \(F\) in N is _________ (round off to the nearest integer).

A cantilever beam (span 1 m) carries a UDL of \(q=1250\) N/m over 0.4 m. A force \(F=1000\) N acts at a distance \(L\) from the fixed end. The distance \(L\) is such that the bending moment at the fixed end is zero. The beam has a rectangular cross-section of depth 20 mm and width 24 mm. Find the maximum bending stress in MPa (round off to nearest integer).

Two identical mass-less beams AB and CD are clamped at their ends.
The left end of beam CD rests on the right end of beam AB at point C (no friction).
A uniformly distributed load of 800 N/m is applied on beam CD of span 1 m.
Find the bending moment at end B of beam AB (in N·m).
Round off to the nearest integer.

The energy equation for a reversible non-flow process can be expressed as \(\delta q = du + p\,dv\), where \(q\) is the heat transfer per unit mass, \(u\) is the internal energy per unit mass, \(p\) is the pressure, and \(v\) is the mass specific volume. This energy equation is not in exact differential form. It can be made exact differential by multiplying with the following integrating factor:
(The temperature \(T\) is absolute temperature)

• (A) \( \dfrac{1}{p} \)
• (B) \( \dfrac{1}{v} \)
• (C) \( \dfrac{1}{T} \)
• (D) \( \dfrac{1}{uT} \)

An air standard Diesel cycle consists of four processes: 1-2 (isentropic compression), 2-3 (constant pressure heat addition), 3-4 (isentropic expansion) and 4-1 (constant volume heat rejection). \(T_4\) is the temperature attained at the end of isentropic expansion (3-4) before constant volume heat rejection. The constant volume heat rejection process (4-1) is replaced by a constant pressure heat rejection process (4a-1) such that \(T_{4a}\) is the temperature reached at the end of isentropic expansion (3-4a), and the state point 1 remains the same. Then

• (A) \(T_{4a} < T_4\)
• (B) \(T_{4a} > T_4\)
• (C) \(T_{4a} = T_4\)
• (D) \(T_{4a} = 2T_4\)

Gas in a cylinder-piston device expands from state 1 \((p_1, V_1, T_1)\) to state 2 \((p_2, V_2, T_2)\). The expansion process is polytropic, i.e., \(pV^n = constant\), \(n \neq 1\). Assuming the ideal gas behaviour, the expression for the work done, \(W\), by the system is given by:

• (A) \(W = p_1 V_1 \ln\!\left(\dfrac{T_2}{T_1}\right)\)
• (B) \(W = \dfrac{p_2 V_2 - p_1 V_1}{1 - n}\)
• (C) \(W = p_1 V_1 \ln\!\left(\dfrac{V_1}{V_2}\right)\)
• (D) \(W = p_2 V_2 \ln\!\left(\dfrac{p_2}{p_1}\right)\)

The temperature of the working fluid in a real heat engine cycle changes during heat addition and heat rejection processes. The maximum and minimum temperatures of the cycle are \(T_{\max}\) and \(T_{\min}\), respectively. If \(\eta_C\) is the thermal efficiency of a Carnot engine operating between these temperature limits, then the thermal efficiency, \(\eta\), of the real heat engine satisfies the relation

• (A) \(\eta > \eta_C\)
• (B) \(\eta < \eta_C\)
• (C) \(\eta = \eta_C\)
• (D) \(\eta = 1 + \eta_C\)

A 1.2 m\(^{3}\) rigid vessel contains 8 kg of saturated liquid–vapor mixture at 150 kPa. The specific enthalpy of this mixture is _________ kJ/kg (round off to 2 decimal places).

At 150 kPa:
\(v_f = 0.001053\) m\(^{3}\)/kg,
\(v_g = 1.1594\) m\(^{3}\)/kg
\(h_f = 467.13\) kJ/kg,
\(h_g = 2693.1\) kJ/kg

Air in a closed system undergoes a thermodynamic process from 300 K to 400 K. The specific heat at constant volume varies linearly with temperature:
\[ c_v = (0.7 + 0.27\times10^{-3} T)\ kJ/(kg·K) \]

Change in specific internal energy is _________ kJ/kg (round off to 2 decimal places).

A vertical cylinder–piston device contains a fixed mass of gas in equilibrium.
Cross-sectional area of the piston is \(A = 0.05\ m^2\).
Gas pressure is 150 kPa.
Find the mass of the piston (kg).
Assume atmospheric pressure = 100 kPa and g = 9.81\ \text{m/s^2.
Round off to 2 decimals.

A steam power plant operates on Rankine cycle.
There is a 20% reduction in net work output (kJ/kg).
Find the percentage increase in specific steam consumption (kg/kJ).
(Answer in integer).

A Carnot heat pump extracts heat from the environment at 250 K and supplies 6 kW of heat to a room maintained at temperature \(T_H\). The heat pump requires a power input of 1 kW. The temperature of the room \(T_H\) is _________ K (round off to nearest integer).

One of the Maxwell equations is expressed as \(\left( \dfrac{\partial s}{\partial v} \right)_{T} = \left( \dfrac{\partial p}{\partial T} \right)_{v}\),
where \(s\) is the entropy per unit mass, \(v\) is the mass specific volume, \(p\) is the pressure, and \(T\) is the temperature.
In this expression, \(s\) is a continuous function of \(T\) and \(v\). Let \(c_v\) be the specific heat capacity at constant volume for a gas.
Then, \(\left( \dfrac{\partial c_v}{\partial v} \right)_{T}\) can be written as

• (A) \( \dfrac{p}{T} \left( \dfrac{\partial^2 p}{\partial T^2} \right)_{v} \)
• (B) \( \dfrac{v}{T} \left( \dfrac{\partial^2 p}{\partial v^2} \right)_{T} \)
• (C) \( T \left( \dfrac{\partial^2 p}{\partial T^2} \right)_{v} \)
• (D) \( \dfrac{1}{T} \left( \dfrac{\partial^2 p}{\partial v^2} \right)_{T} \)

The general relation among the properties \(x\), \(y\) and \(z\) at any state point can be expressed as \[ \left( \frac{\partial x}{\partial y} \right)_z \left( \frac{\partial y}{\partial z} \right)_x \left( \frac{\partial z}{\partial x} \right)_y = -1 . \]
If \(p\), \(T\) and \(h\) are continuous functions and \[ c_p = \left( \frac{\partial h}{\partial T} \right)_p , \]
and \(\mu\) is the Joule–Thomson coefficient, then \[ \left( \frac{\partial h}{\partial p} \right)_T \]
is:

• (A) \(- \mu c_p\)
• (B) \(c_p T\)
• (C) \(-\dfrac{c_p}{T}\)
• (D) \(\mu c_p\)

An air-conditioning system consists of an insulated rigid mixing chamber designed to supply air at 24 °C to a building. The mixing chamber mixes two air streams: (i) a cold air stream at 10 °C and mass flow rate \(\dot{m}_c\) (kg/s), and (ii) a stream of fresh ambient air at 30 °C and mass flow rate \(\dot{m}_a\) (kg/s). Assume air to be an ideal gas with constant specific heat (\(c_p = 1.005\) kJ/(kg K), \(\gamma = c_p/c_v = 1.4\)). Neglect change in kinetic and potential energies as compared to change in enthalpy. Under the steady state condition, the ratio of the mass flow rates of the two streams \((\dot{m}_c/\dot{m}_a)\) is:

• (A) \(\dfrac{7}{3}\)
• (B) \(\dfrac{3}{7}\)
• (C) \(\dfrac{2}{7}\)
• (D) \(\dfrac{4}{7}\)

An ideal gas mixture consists of 80% N\(_2\) and 20% O\(_2\) on mass basis. If the total pressure is 300 kPa, then the partial pressure of N\(_2\) (in kPa) is

(Molecular weights of N\(_2\) = 28 kg/kmol and O\(_2\) = 32 kg/kmol)

• (A) 246.15
• (B) 230.34
• (C) 254.78
• (D) 213.54

On the basis of the ideal gas equation and van der Waals equation, the temperatures of a gas at pressure 10 MPa and specific volume 0.005 m\(^3\)/kg would be, respectively

(Assume gas constant \(R = 0.3\) kJ/(kg K), \(a = 0.18\) m\(^6\) kPa/kg\(^2\) and \(b = 0.0014\) m\(^3\)/kg)

• (A) 166.67 K and 235.89 K
• (B) 166.67 K and 206.40 K
• (C) 166.67 K and 267.21 K
• (D) 166.67 K and 240.90 K

An ideal Brayton cycle operates between maximum and minimum temperatures of \( T_3 \) and \( T_1 \), respectively. For constant values of \( T_3 \) and \( T_1 \), the pressure ratio \( r_p \) for maximum work output is:

• (A) \( \left(\frac{T_3}{T_1}\right)^{\frac{\gamma}{\gamma-1}} \)
• (B) \( \left(\frac{T_3}{T_1}\right)^{\frac{2\gamma}{\gamma-1}} \)
• (C) \( \left(\frac{T_3}{T_1}\right)^{\frac{\gamma}{\gamma-1}} \)
• (D) \( \left(\frac{T_3}{T_1}\right)^{\frac{2}{\gamma-1}} \)

An insulated rigid tank of volume 10 m\(^3\) contains air initially at 1 MPa and 600 K. A valve connected to the tank is opened, and air is allowed to escape until the temperature inside the tank drops to 400 K. The temperature of the discharged air can be approximated as the average of the initial and final temperatures of the air in the tank. Neglect kinetic and potential energies of the discharged air. Assume that air behaves as an ideal gas with constant specific heat so that internal energy \(u = c_p T\) and enthalpy \(h = c_p T\). Then, the final pressure of the air in the tank is _________ MPa (round off to 2 decimal places).

Assume: \(c_p = 1.005\) kJ/(kg K), \(\gamma = \frac{c_p}{c_v} = 1.4\)

Steam enters a steam turbine at 5 MPa and 600°C, and exits as saturated vapor at 50 kPa. Under steady state condition, the turbine loses heat to the surroundings at the rate of 50 kJ per kilogram of steam flowing through the turbine. The ambient temperature is 300 K, and the heat transfer to the surroundings takes place at the outer surface of the turbine at a temperature of 450 K. The irreversibility per unit mass of steam flowing through the turbine is _________ kJ/kg (round off to 2 decimal places).

A heat engine receives heat at 1000 K and rejects heat to environment at 300 K.
Its efficiency is half that of a Carnot engine operating between these temperatures.
The work output drives a refrigerator removing heat from a cold space at 260 K at 5.2 kW,
rejecting heat at 300 K.
The refrigerator COP is half of the Carnot refrigerator.
Find the rate of heat supplied to the heat engine (kW).
Round off to 2 decimals.

A room contains air at 25°C, 100 kPa and 80% relative humidity.
Saturation pressure of water vapor at 25°C is 3.1698 kPa.
Find the specific humidity (kg water vapor/kg dry air).
Round off to 4 decimals.

An insulated rigid container is divided into two parts by a thin partition. One part of the container contains 6 kg of saturated liquid-vapor mixture with a dryness fraction of 0.7 at 0.3 MPa. The other part contains 12 kg of saturated liquid at 0.6 MPa of the same substance. When the partition is removed and the system attains equilibrium, the final specific volume of the mixture is _________ m\(^3\)/kg (round off to 2 decimal places).

During a steady state air-conditioning process, air enters a heating section at 15°C with 40% relative humidity and leaves at 30°C. Assuming the heating process takes place at 100 kPa, the relative humidity of the air at exit is _________ % (round off to nearest integer).

Saturation pressures of water vapor at 15°C and 30°C are 1.7057 kPa and 4.2469 kPa respectively.

Steam enters a steam turbine at 10 MPa and 600°C with a mass flow rate of 16 kg/s.
The steam exits the turbine as saturated vapor at 10 kPa.
Under steady state condition, the turbine generates 16.2 MW power.
If the ambient temperature is 25°C, the rate of entropy generation in the turbine is _________ kW/K (round off to 2 decimal places).

Interfacial polymerization can be used to prepare

• (A) Nylon 6
• (B) Nylon 66
• (C) Polyacrylonitrile
• (D) Poly(butyl acrylate)

In a rubber sample with a Mooney viscosity of 60 ML(1+4) 100°C, the number 4 signifies

• (A) Applied shear rate in s\(^{-1}\)
• (B) Number of samples tested
• (C) Time in minutes after starting the motor when the measurement is taken
• (D) Preheating time in minutes

The initiator system which can be used for free radical polymerization at 5°C is:

• (A) FeSO4 + t-butyl hydroperoxide
• (B) Azobisisobutyronitrile
• (C) Potassium persulfate
• (D) Benzoyl peroxide

Weather resistance of high impact polystyrene can be improved by blending polystyrene with:

• (A) Styrene butadiene rubber
• (B) Natural rubber
• (C) Ethylene propylene rubber
• (D) Nitrile rubber

Which of the following is a discontinuous polymer processing operation?

• (A) Calendering
• (B) Extrusion
• (C) Film blowing
• (D) Thermoforming

The blend of polyethylene and polypropylene is:

• (A) Immiscible due to enthalpic constraints
• (B) Immiscible due to entropic constraints
• (C) Miscible as they are polyolefins
• (D) Miscible due to comparable solubility parameters

Toughness in a polymer can be inferred from

• (A) Izod impact strength
• (B) Depth of indentation
• (C) Area under the stress-strain curve
• (D) Charpy impact strength

Which of the following polymers are polyesters?

• (A) Poly(acrylic acid)
• (B) Poly(lactic acid)
• (C) Polyhydroxybutyrate
• (D) Poly(\(\varepsilon\)-caprolactone)

The functionality of adipic acid for condensation reaction with glycerol is _________ (in integer).

From the dynamic mechanical analysis of a polymer sample with a phase angle of 30°, the relationship between storage modulus \( E' \) and loss modulus \( E'' \) can be expressed as:

• (A) \( E' = \sqrt{3} E'' \)
• (B) \( 2E' = \sqrt{3} E'' \)
• (C) \( E'' = \sqrt{3} E' \)
• (D) \( 2E'' = \sqrt{3} E' \)

Match the properties in Column A with their respective unit in Column B:

• (A) P-1; Q-3; R-4; S-2
• (B) P-2; Q-3; R-1; S-4
• (C) P-3; Q-1; R-2; S-4
• (D) P-3; Q-1; R-2; S-4

Match the following polymer product with its most appropriate processing technique



\begin{tabbing
\hspace{5cm \= \hspace{3cm \= \hspace{2cm \= \kill
Polymer product \> Processing technique

P. Bottle \> 1. Extrusion

Q. Blister packaging \> 2. Pultrusion

R. Reinforced electric poles \> 3. Injection blow molding

S. Sewage pipes \> 4. Thermoforming

\end{tabbing

• (A) P-3; Q-4; R-1; S-2
• (B) P-3; Q-4; R-2; S-1
• (C) P-4; Q-3; R-1; S-1
• (D) P-3; Q-2; R-4; S-1

Match the following additives to their respective functions:

• (A) P-4; Q-2; R-1; S-3
• (B) P-3; Q-1; R-2; S-4
• (C) P-4; Q-1; R-3; S-2
• (D) P-4; Q-1; R-2; S-3

Match the polymers with their characteristic infrared (IR) stretching frequency.

• (A) P-4; Q-3; R-2; S-1
• (B) P-3; Q-4; R-2; S-1
• (C) P-3; Q-4; R-1; S-2
• (D) P-3; Q-2; R-4; S-1

Match the following polymers to the most appropriate product

• (A) P-2; Q-1; R-4; S-3
• (B) P-2; Q-4; R-1; S-3
• (C) P-3; Q-1; R-2; S-4
• (D) P-3; Q-1; R-4; S-2

Match the polymers to the polymerization method used for their synthesis:

• (A) P-2; Q-1; R-4; S-3
• (B) P-2; Q-1; R-3; S-4
• (C) P-2; Q-3; R-4; S-1
• (D) P-2; Q-4; R-1; S-3

If 5 g of a monodisperse polystyrene sample of molecular weight 10,000 g mol\(^{-1}\) is mixed with 15 g of another monodisperse polystyrene sample of molecular weight 20,000 g mol\(^{-1}\), then the polydispersity of the resulting mixture is _________ (rounded off to two decimal places).

For a polymer sample with a viscosity of \(6 \times 10^{11}\) poise, if the apparent plateau modulus of \(3 \times 10^6\) dyne cm\(^{-2}\) drops to zero above a certain temperature, the relaxation time of the polymer is _________ days (rounded off to one decimal place).

The thermal conductivity values of glass fiber and epoxy resin are 1.05 W m^{-1 \text{K^{-1 and 0.25 W m^{-1 \text{K^{-1, respectively.
The thermal conductivity of a glass fiber reinforced epoxy composite with a fiber content of 60% by volume along the fiber direction is _________ \text{ W m^{-1 \text{K^{-1 . (Round off to two decimal places).

The tensile modulus of a thermosetting polyester resin and glass fiber are 3 GPa and 80 GPa, respectively.
If a tensile stress of 110 MPa is applied along the fiber direction on a continuous uniaxially aligned glass fiber reinforced thermosetting polyester composite with a fiber content of 60% by volume, the resulting strain will be _________ \times 10^{-3 \text{ (round off to one decimal place).

The amount of low molecular weight plasticizer with a \(T_g\) of -60°C that must be added to nylon 6 to reduce its \(T_g\) from 50°C to 30°C is _________ % (rounded off to nearest integer).

The enthalpy of fusion for a polymer is found to decrease from 135.6 J g\(^{-1}\) to 120 J g\(^{-1}\) after five years of use. If the enthalpy of fusion of the same polymer with 100% crystallinity is 290 J g\(^{-1}\), then the loss in crystallinity after five years is _________ % (rounded off to one decimal place).

Which among the given options truly depict the lines 1 and 2 in the figure below with respect to the effect of heat processing on food?

• (A) 1-Safety, 2-Quality
• (B) 1-Yield, 2-Safety
• (C) 1-Yield, 2-Quality
• (D) 1-Quality, 2-Safety

Homogenization of milk leads to disintegration of fat globules by

• (A) Turbulence and pasteurization
• (B) Pasteurization and cavitation
• (C) Pasteurization and pressurization
• (D) Turbulence and cavitation

The lowest water activity (\(a_w\)) supporting the growth of Staphylococcus aureus in food under aerobic condition is:

• (A) 0.98
• (B) 0.91
• (C) 0.89
• (D) 0.86

Cultures used in industrial production of yogurt are:

• (A) Lactococcus lactis subsp. lactis
• (B) Streptococcus thermophilus
• (C) Leuconostoc mesenteroides subsp. cremoris
• (D) Lactobacillus delbrueckii subsp. bulgaricus

In a dairy plant, spray drying technology is used to produce whey powder. The rate of spray drying depends on:

• (A) Temperature of the incoming air
• (B) Shape of the cyclone separator
• (C) Diameter of the whey droplet
• (D) Heat transfer coefficient of hot air

The parboiling of paddy results into:

• (A) Increase in the milling losses
• (B) Increase in the nutritional value of rice
• (C) Increase in the head rice recovery
• (D) Increase in the broken rice percentage

One hundred kg paddy is dried from 18% wet basis to 13% wet basis moisture content. The amount of water removed (in kg) from the paddy is _________ (round off to one decimal place).

The radius of a centrifuge bowl is 0.1 m and is rotating at 850 revolutions per minute. The centrifugal force developed in terms of gravity force (g-force) is _________ (round off to two decimal places).

Given: Acceleration of gravity (g) = 9.81 m/s\(^2\) and \(\pi = 3.14\)

In a canning industry, the total process time \( F_0 \) was calculated as 3 min.
If each can contains 20 spores with decimal reduction time of 1.6 min, the probability of spoilage would be _________ \text{ in 100 cans. (round off to the nearest integer)

Match the edible oil refining stages given in Column I with their respective functions in Column II

• (A) P-3, Q-2, R-1, S-4
• (B) P-2, Q-1, R-3, S-4
• (C) P-3, Q-4, R-2, S-1
• (D) P-3, Q-1, R-2, S-4

Make the correct pair of food packaging technology given in Column I with operating principle or description in Column II

• (A) P-3, Q-1, R-2
• (B) P-2, Q-4, R-1
• (C) P-1, Q-3, R-2
• (D) P-3, Q-2, R-1

Which of the following is not a caramel flavour producing compound?

• (A) 3-Hydroxy-2-methylpyran-4-one
• (B) 2H-4-Hydroxy-5-methylfuran-3-one
• (C) 3-Hydroxy-2-acetylfuran
• (D) p-Amino benzoic acid

Match the size reduction equipment in Column I with the method of operation in Column II:

• (A) P-2; Q-4; R-1; S-3
• (B) P-3; Q-1; R-2; S-4
• (C) P-4; Q-1; R-2; S-3
• (D) P-3; Q-4; R-2; S-1

Most commonly used refrigerant in direct immersion freezing of food is

• (A) Monochlorodifluoromethane
• (B) Dichlorodifluoromethane
• (C) Liquid nitrogen
• (D) Freon

Which among the following are \(\omega\)-6 polyunsaturated essential fatty acids?

• (A) 18:2 Linoleic acid
• (B) 18:3 \(\alpha\)-Linolenic acid
• (C) 18:3 \(\gamma\)-Linolenic acid
• (D) 20:4 Arachidonic acid

Which among the following statements are true with respect to protein denaturation?

• (A) There may be an increase in \(\alpha\)-helix and \(\beta\)-sheet structure
• (B) It is an irreversible process
• (C) When fully denatured, globular proteins resemble a random coil
• (D) The peptide bonds are broken

Identify the correct pair(s) of milling equipment and the grain for which it is used.

• (A) Mist polisher–Rice
• (B) Break roll–Wheat
• (C) Rubber roll–Pigeon pea
• (D) Beall degermmer–Maize

Which among the following expression(s) is/are correct?

• (A) Reynolds number = \(\dfrac{Density \times Velocity \times Characteristic dimension}{Viscosity}\)
• (B) Nusselt number = \(\dfrac{Convective heat transfer coefficient \times Characteristic dimension}{Thermal conductivity of solid}\)
• (C) Schmidt number = \(\dfrac{Kinematic viscosity of fluid}{Diffusivity}\)
• (D) Biot number = \(\dfrac{Convective heat transfer coefficient \times Characteristic dimension}{Thermal conductivity of fluid}\)

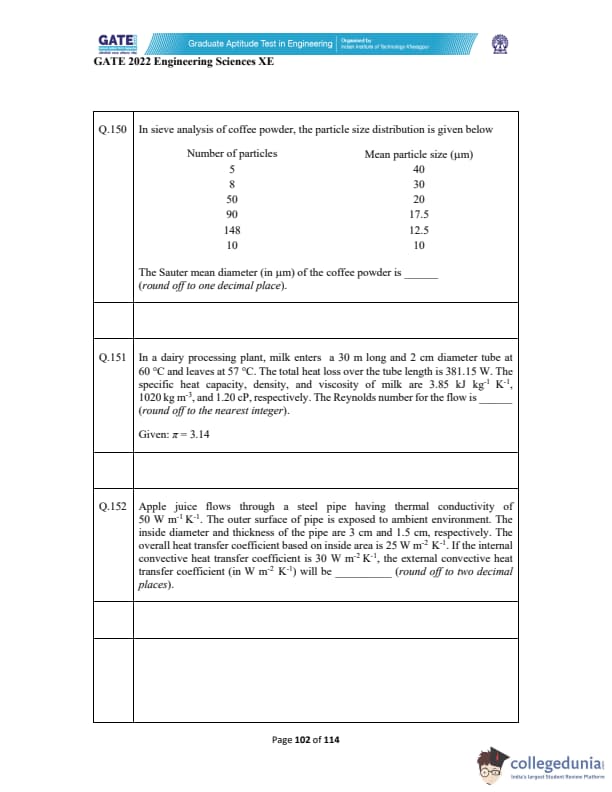
In sieve analysis of coffee powder, the particle size distribution is given below:



The Sauter mean diameter (in µm) of the coffee powder is _________ (round off to one decimal place).

In a dairy processing plant, milk enters a 30 m long and 2 cm diameter tube at 60°C and leaves at 57°C. The total heat loss over the tube length is 381.15 W. The specific heat capacity, density, and viscosity of milk are 3.85 kJ kg\(^{-1}\) K\(^{-1}\), 1020 kg m\(^{-3}\), and 1.20 cP, respectively. The Reynolds number for the flow is _________ (rounded off to the nearest integer).

Given: Acceleration of gravity \( g = 9.81 \ m/s^2 \) and \( \pi = 3.14 \)

Apple juice flows through a steel pipe having thermal conductivity of 50 W m^{-1 \text{K^{-1 .
The outer surface of the pipe is exposed to ambient environment.
The inside diameter and thickness of the pipe are 3 cm and 1.5 cm, respectively.
The overall heat transfer coefficient based on inside area is 25 W m^{-2 \text{K^{-1. If the internal convective heat transfer coefficient is 30 W m^{-2 \text{K^{-1, the external convective heat transfer coefficient (in W m^{-2 \text{K^{-1 ) will be _________ (round off to two decimal places).

The dry bulb temperature and relative humidity of air inside a storage chamber are 37°C and 50%, respectively.
The saturation pressure of water vapour at 37°C and barometric pressure are 6.28 kPa and 101.32 kPa, respectively.
The humidity ratio of air inside the chamber is _________ \text{ kg water / kg dry air. (Round off to three decimal places.)

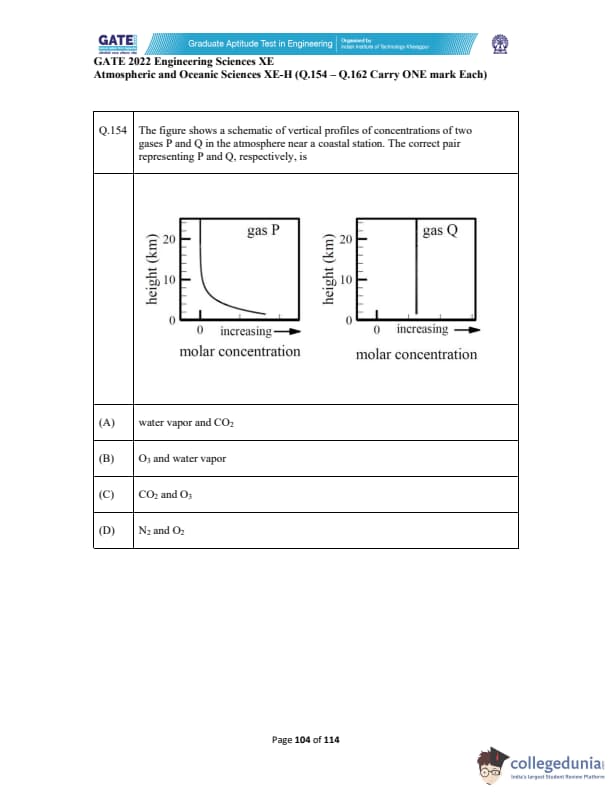
The figure shows a schematic of vertical profiles of concentrations of two gases P and Q in the atmosphere near a coastal station. The correct pair representing P and Q, respectively, is

• (A) Water vapor and CO\(_2\)
• (B) O\(_3\) and water vapor
• (C) CO\(_2\) and O\(_3\)
• (D) N\(_2\) and O\(_2\)

A form of momentum equation for an incompressible fluid is

\[ \rho \frac{D \mathbf{V}}{Dt} = -\nabla p + \mu \nabla^2 \mathbf{V} + \mathbf{B} \]
where \( \rho \) is density, \( \mathbf{V} \) is velocity, \( t \) is time, \( p \) is pressure, \( \mu \) is viscosity, and \( \mathbf{B} \) represents body force per unit volume. The dimension of term (iii) is:

• (A) \( [L]^1 [T]^{-2} \)
• (B) \( [M]^1 [L]^{-2} [T]^{-2} \)
• (C) \( [M]^1 [L]^1 [T]^{-2} \)
• (D) \( [M]^1 [L]^1 [T]^{-1} \)

Tropical cyclones usually do not form close to the Equator primarily because

• (A) sea surface temperature at the Equator is too cold.
• (B) beta effect dissipates clouds.
• (C) Coriolis force is too weak.
• (D) vertical shear of the zonal wind is weak.

Which one of the following statements regarding equatorial undercurrent (EUC) in the Pacific Ocean is correct?

• (A) EUC flows from west to east.
• (B) EUC flows from east to west.
• (C) EUC flows from north to south.
• (D) EUC flows from south to north.

Which one of the following statements is correct regarding the dominant energy balance in the troposphere in a tropical convergence zone?

• (A) Shortwave heating balances longwave radiative cooling.
• (B) Compressional heating balances radiative cooling.
• (C) Radiative cooling balances heating due to viscous dissipation of kinetic energy.
• (D) Condensational heating balances adiabatic cooling.

Which one of the following processes is primarily responsible for the poleward transport of energy in the midlatitude troposphere?

• (A) Atmospheric tides
• (B) Baroclinic waves
• (C) Gravity waves
• (D) Turbulence in the boundary layer

Which of the following feature(s) characterize the seasonal mean flow in the upper troposphere near 200 hPa level over the Tibetan Plateau during the boreal summer?

• (A) Cyclonic
• (B) Anticyclonic
• (C) Irr rotational
• (D) Divergent

The Rossby number of a synoptic system with a length scale of 1000 km, characteristic velocity scale of 10 m s\(^{-1}\) at a latitude where the Coriolis parameter equals \(10^{-4}\) s\(^{-1}\), is _________ (rounded off to two decimal places).

The ratio of scattering efficiency of red light of wavelength 0.65 µm to blue light of wavelength 0.45 µm by air molecules in the atmosphere is _________ (rounded off to two decimal places).

An unsaturated moist air parcel undergoes adiabatic ascent in the atmosphere without mixing with surrounding air. Air is so clean that there is no possibility for heterogeneous nucleation. Which one of the following plots depicts the vertical variation of water vapor pressure (shown as continuous line) and saturation water vapor pressure (shown as dotted/dashed line) of the parcel?

• (A) P
• (B) Q
• (C) R
• (D) S

A fluid is in solid body rotation in a cylindrical container of radius \(R\) rotating with an angular velocity \(\Omega = (0, 0, \Omega)\). The circulation per unit area around a circular loop in the horizontal plane of radius \(r\) (\(r < R\)), whose center coincides with the axis of rotation is

• (A) \(r \Omega\)
• (B) \(r \Omega^2\)
• (C) \(r^2 \Omega\)
• (D) \(r^2 \Omega^2\)

Consider a layer of atmosphere where temperature increases with height. If the concentration of a vertically well-mixed greenhouse gas suddenly increases in this layer, then an immediate consequence is that:

• (A) infrared radiation leaving the top of the layer decreases.
• (B) infrared radiation leaving the top of the layer increases.
• (C) infrared radiation leaving the top of the layer remains unchanged.
• (D) the layer becomes optically thinner to infrared radiation.

Consider an atmosphere where the mole fractions of \( N_2 \), \( Ar \), and \( CO_2 \) are \( 7.81 \times 10^{-1} \), \( 9.34 \times 10^{-3} \), and \( 4.05 \times 10^{-4} \), respectively. This atmosphere exchanges gases with sea water below having temperature and salinity of 20°C and 35 psu, respectively. In the absence of biological and chemical activity, relative concentrations of dissolved gases in the surface sea water at equilibrium are ordered as:

• (A) \( [N_2] > [Ar] > [CO_2] \)
• (B) \( [CO_2] > [N_2] > [Ar] \)
• (C) \( [N_2] > [CO_2] > [Ar] \)
• (D) \( [Ar] > [CO_2] > [N_2] \)

Gravitational forces exerted by the Sun and the Moon are mainly responsible for ocean tides. Which of the following statement(s) regarding ocean tides is/are correct?

• (A) Tidal amplitude corresponding to diurnal period is larger than that of the semi-diurnal period.
• (B) Diurnal time period of lunar forced tides is longer than that of the solar forced tides.
• (C) Tidal amplitudes are larger during a solar eclipse compared to that during a lunar eclipse.
• (D) Tides are absent during equinoxes.

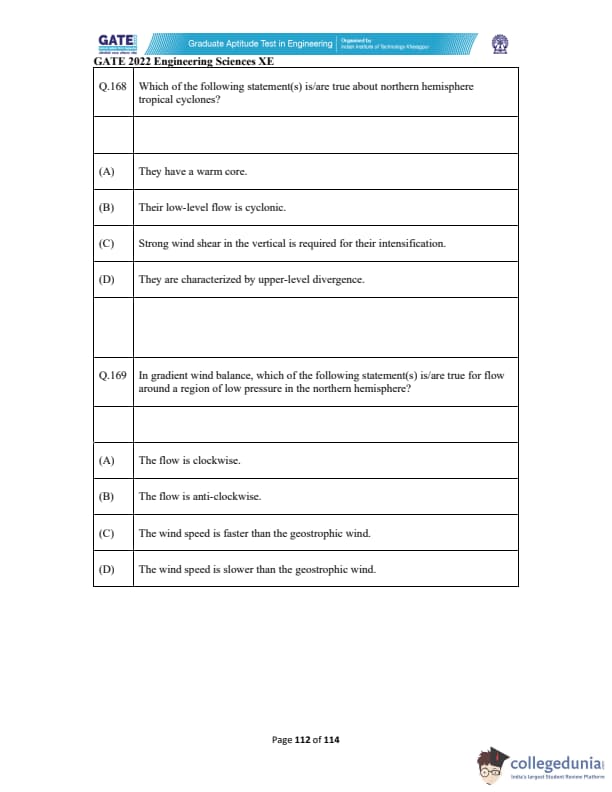
Which of the following statement(s) is/are true about northern hemisphere tropical cyclones?

• (A) They have a warm core.
• (B) Their low-level flow is cyclonic.
• (C) Strong wind shear in the vertical is required for their intensification.
• (D) They are characterized by upper-level divergence.

In gradient wind balance, which of the following statement(s) is/are true for flow around a region of low pressure in the northern hemisphere?

• (A) The flow is clockwise.
• (B) The flow is anti-clockwise.
• (C) The wind speed is faster than the geostrophic wind.
• (D) The wind speed is slower than the geostrophic wind.

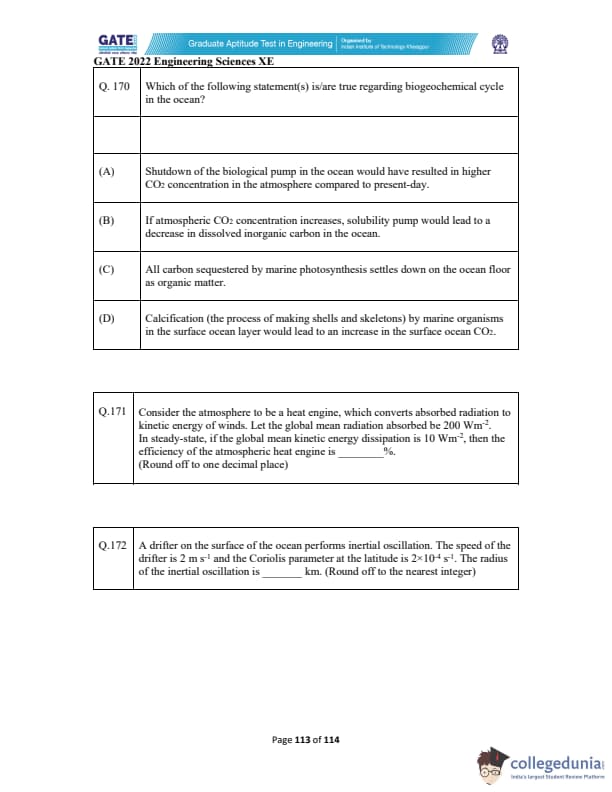
Which of the following statement(s) is/are true regarding the biogeochemical cycle in the ocean?

• (A) Shutdown of the biological pump in the ocean would have resulted in higher CO₂ concentration in the atmosphere compared to present-day.
• (B) If atmospheric CO₂ concentration increases, the solubility pump would lead to a decrease in dissolved inorganic carbon in the ocean.
• (C) All carbon sequestered by marine photosynthesis settles down on the ocean floor as organic matter.
• (D) Calcification (the process of making shells and skeletons) by marine organisms in the surface ocean layer would lead to an increase in the surface ocean CO₂.

Consider the atmosphere to be a heat engine, which converts absorbed radiation to kinetic energy of winds. Let the global mean radiation absorbed be 200 Wm\(^{-2}\). In steady-state, if the global mean kinetic energy dissipation is 10 Wm\(^{-2}\), then the efficiency of the atmospheric heat engine is _________% (round off to one decimal place).

A drifter on the surface of the ocean performs inertial oscillation. The speed of the drifter is 2 m s\(^{-1}\) and the Coriolis parameter at the latitude is \(2 \times 10^{-4}\) s\(^{-1}\). The radius of the inertial oscillation is _________ km. (Round off to the nearest integer)

Consider a tornado in cyclostrophic balance. The tangential wind speed at a radial distance of 500 m from the center of the tornado is _________ \text{m/s, if the pressure gradient at that location in the radial direction is 5 N/m^3. Assume the density of air to be 1 kg/m^3 . (Round off to the nearest integer).

Consider two weather stations A and B having the same altitude. Station B is 5 km north of Station A and is always 2 K warmer than Station A. A steady northerly wind blows at 1 m/s. The change in temperature at Station A in 2 hours is _________ \text{ K. (Round off to one decimal place).

Assume the Earth is in radiative equilibrium with an effective radiative temperature of 255 K.
If the planetary albedo increases by 0.05, then the effective radiative temperature of the planet will be _________ \text{ K. (Round off to the nearest integer)