GATE 2022 Production and Industrial Engineering (PI) Question Paper with Solutions pdf is available for download. The exam was conducted by Indian Institute of Technology Kharagpur on Feb-06 in the Afternoon Session. In terms of difficulty level, GATE Production and Industrial Engineering- PI was of Moderate level. The question paper comprised a total of 65 questions from General Aptitude and Production and Industrial Engineering- PI topics.
GATE 2022 Production and Industrial Engineering (PI) Question Paper with Solutions
| GATE 2022 Production and Industrial Engineering (PI) Question Paper | Check Solutions |

Inhaling the smoke from a burning __________ could __________ you quickly.
A sphere of radius \(r\) cm is packed in a box of cubical shape.
What should be the minimum volume (in cm\(^3\)) of the box that can enclose the sphere?
Pipes P and Q can fill a storage tank in full with water in 10 and 6 minutes, respectively. Pipe R draws the water out from the storage tank at a rate of 34 litres per minute. P, Q and R operate at a constant rate.
If it takes one hour to completely empty a full storage tank with all the pipes operating simultaneously, what is the capacity of the storage tank (in litres)?
Six persons P, Q, R, S, T, and U are sitting around a circular table facing the center not necessarily in the same order. Consider the following statements:
P sits next to S and T.
Q sits diametrically opposite to P.
The shortest distance between S and R is equal to the shortest distance between T and U.
Based on the above statements, Q is a neighbor of
A building has several rooms and doors as shown in the top view of the building given below. The doors are closed initially.
What is the minimum number of doors that need to be opened in order to go from the point P to the point Q?

Rice, a versatile and inexpensive source of carbohydrate, is a critical component of diet worldwide. Climate change, causing extreme weather, poses a threat to sustained availability of rice. Scientists are working on developing Green Super Rice (GSR), which is resilient under extreme weather conditions yet gives higher yields sustainably.
Which one of the following is the CORRECT logical inference based on the information given in the above passage?
A game consists of spinning an arrow around a stationary disk as shown below.
When the arrow comes to rest, there are eight equally likely outcomes. It could come to rest in any one of the sectors numbered 1, 2, 3, 4, 5, 6, 7, or 8 as shown.
Two such disks are used in a game where their arrows are independently spun.
What is the probability that the sum of the numbers on the resulting sectors upon spinning the two disks is equal to 8 after the arrows come to rest?

Consider the following inequalities.
(i) \( 3p - q < 4 \)
(ii) \( 3q - p < 12 \)
Which one of the following expressions below satisfies the above two inequalities?
Given below are three statements and four conclusions drawn based on the statements.
Statement 1: Some engineers are writers.
Statement 2: No writer is an actor.
Statement 3: All actors are engineers.
Conclusion I: Some writers are engineers.
Conclusion II: All engineers are actors.
Conclusion III: No actor is a writer.
Conclusion IV: Some actors are writers.
Which one of the following options can be logically inferred?
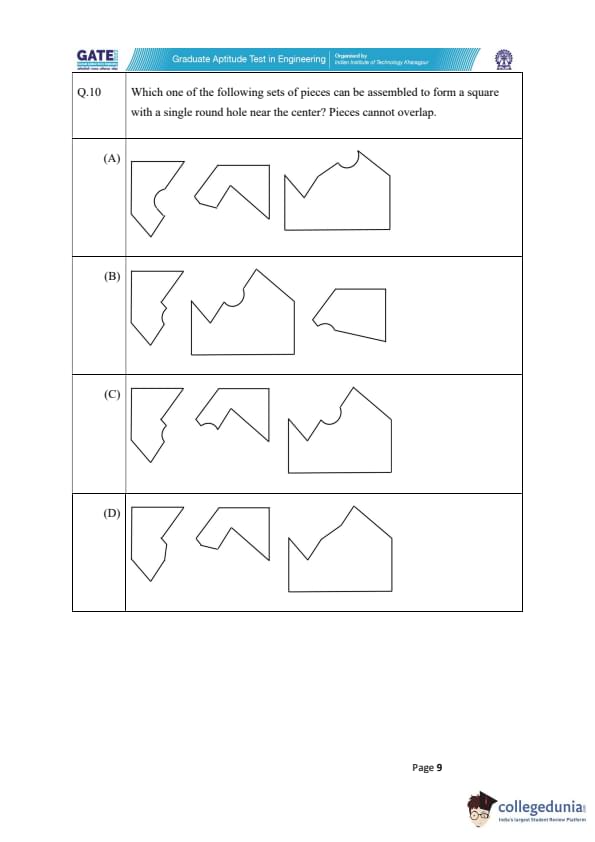
Which one of the following sets of pieces can be assembled to form a square with a single round hole near the center? Pieces cannot overlap.

If \(\mathbf{a}\), \(\mathbf{b}\) and \(\mathbf{c}\) are three vectors, the vector triple product \((\mathbf{a}\times\mathbf{b})\times\mathbf{c}\) is given by
The numerical integration of the function \(y = 2x + 5\) is carried out between \(x = 1\) and \(x = 3\), by using ordinates at \(x = 1, 2,\) and \(3\). Which one of the following statements is TRUE?
Which one of the following metals has a face-centered cubic (FCC) structure?
If \( G \) denotes the shear modulus of an isotropic material, then the maximum possible value of Young's modulus of the material is
Match the casting methods with products.

In injection blow molding of plastic beverage bottles, the blowing is accomplished by
In an electro-discharge machining process, the discharge voltage is \(V_b\). The energy dissipated per spark across the inter-electrode gap is proportional to
Match the codes used in CNC part programming with their functions.

The control chart for a number of defects in a welded joint is
Which one of the following statements is TRUE?
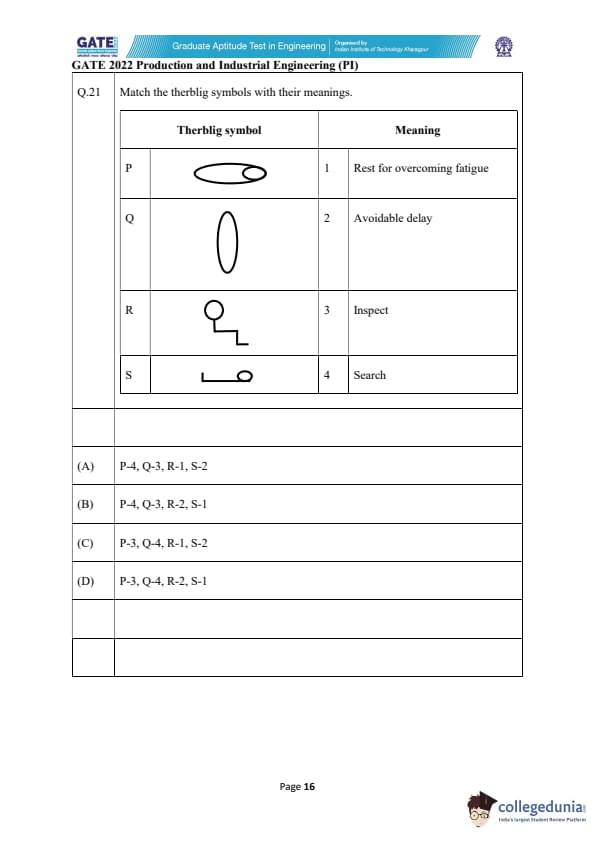
Match the therblig symbols with their meanings.

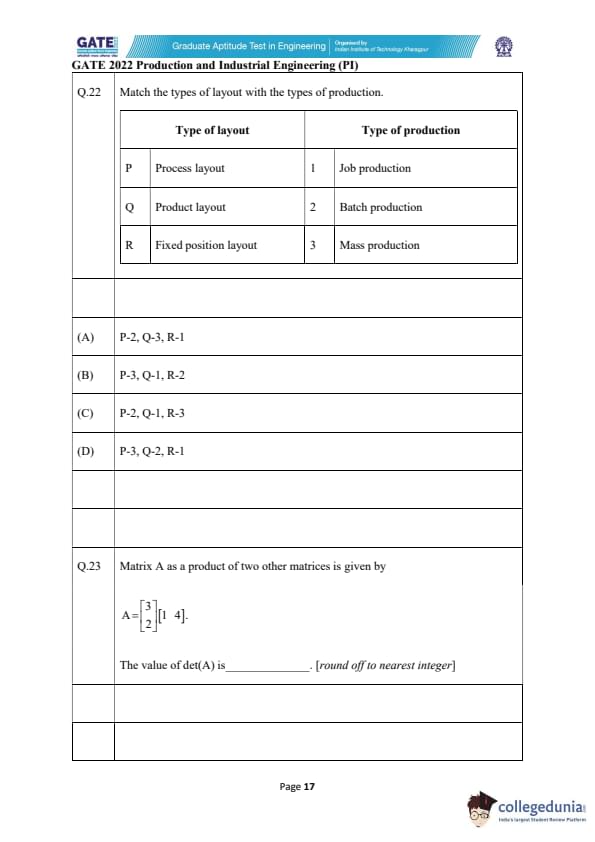
Match the types of layout with the types of production.

Matrix A as a product of two other matrices is given by \[ A=\begin{bmatrix} 3
[4pt] 2 \end{bmatrix} \begin{bmatrix} 1\;\;4 \end{bmatrix}. \]
The value of det(A) is __________ (round off to nearest integer).
The order of the following differential equation is ________. [in integer] \[ \left(\frac{dy}{dx}\right)^{2} + 5\frac{dy}{dx} + 4y = 5x^{3} \]
An operator manufactures 10 identical spur gears in a lot. One spur gear is defective. Three spur gears are drawn at random without replacement. The probability of getting all three gears as non-defective is ________. [round off to two decimal places]
In a slider–crank mechanism, the crank rotates at 60 rpm. The crank radius is 30 mm and the connecting rod length is 120 mm. The average speed (in mm/s) of the piston over one revolution of the crank is ________ (round off to nearest integer).

Water with kinematic viscosity \(\nu = 1\times10^{-6}\ m^2/s\) flows through a circular pipe of diameter 8 mm. If flow is laminar and fully developed with maximum velocity 0.5 m/s, the Reynolds number is ________ (round off to nearest integer).
Yielding starts in a material when the principal stresses are 100 MPa, 100 MPa and 200 MPa. As per the von Mises criterion, yield stress (in MPa) of the material is ________. [round off to nearest integer]
A single-point cutting tool with zero rake angle is used for orthogonal machining. If the chip-compression ratio is 1.25, then the shear angle (in degree) during machining is _______. [round off to one decimal place]
It is required to cut a single-start thread of 2 mm pitch in a lathe machine with a single-start lead screw of 4 mm pitch. For one revolution of the workpiece, the number of revolutions of the lead screw is _________ (round off to two decimal places).
The absolute deviations of 8 points from the datum line of a surface are 10, 15, 12, 10, 13, 12, 20 and 25 μm. The root mean square value of the surface roughness (in μm) is _________ (round off to one decimal place).
In a machine there are two motors, but only one motor is needed for the functioning of the machine. The reliabilities of the motors are 0.90 and 0.70. The overall reliability of the machine is ________. [round off to two decimal places]
If the interarrival time is exponential and 8 customers per hour arrive in a bank, then the probability of no arrival of customer during a period of 15 minutes is ________. [round off to two decimal places]
A company buys a machine worth ₹65000, which has a salvage value of ₹5000. The annual depreciation cost is ₹10000 based on the straight-line depreciation method. The useful life (in years) of the machine is _________ (in integer).
A project comprises of seven activities. The expected durations of activities and their variances are as follows:

The critical path consists of activities B, E and G. The standard deviation (in minute) of the project duration is ________. [round off to two decimal places]
If a matrix is squared, then
Consider the following ordinary differential equation:
\[ 4 \frac{d^{2} y}{dx^{2}} - 4 \frac{dy}{dx} + y = 0. \]
Given that \( c_{1} \) and \( c_{2} \) are constants, the general solution of the differential equation is
A market survey with a sample size of 1000 was conducted for a parameter that follows normal distribution. The confidence interval was estimated as [500, 700] with a mean of 600. It is now desired to reduce the confidence interval to [550, 650]. The sample size for achieving the desired interval at the same confidence level is
A eutectoid steel with 100% austenite is cooled from a temperature of 750\,°C to a room temperature of 35\,°C. Match the cooling methods with the transformed structures.

In the three-member truss shown in the figure, AC = BC. An external force of 10 kN is applied at B, parallel to AC. The force in the member BC is

Match the processing steps related to production of powder metallurgy parts with their descriptions.

In an assembly comprising shaft and hole, the nominal sizes with tolerances are specified as
Hole: \(25.000^{+0.002}_{-0.001}\) mm,
Shaft: \(25.000^{+0.001}_{-0.003}\) mm.
The type of fit is
In a manufacturing system, four different types of products (P, Q, R and S) are produced. The batch size of each product is \(2 \times 10^{7}\). The numbers of defective units are 60, 71, 80 and 55, for P, Q, R and S, respectively. Which one of the following statements is TRUE?
Match the processes of product development with their characteristics.

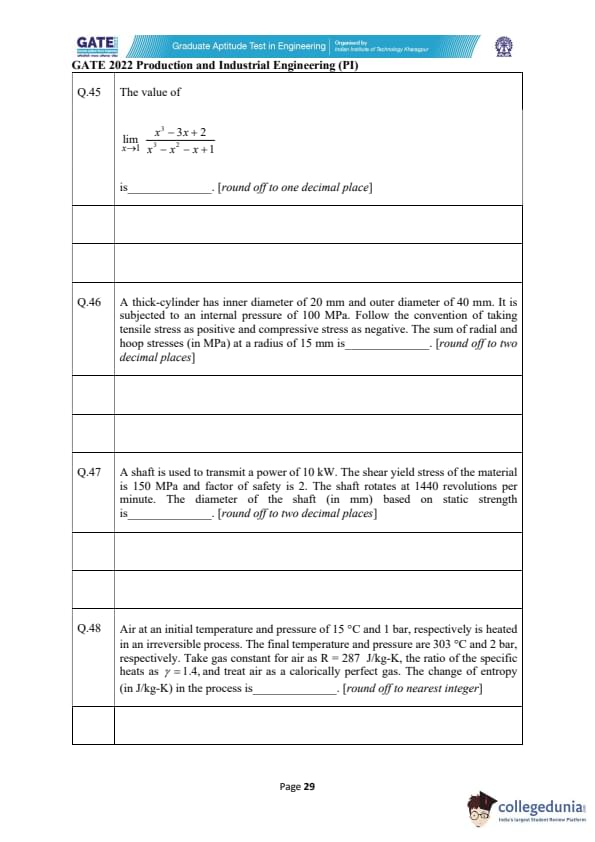
The value of \[ \lim_{x \to 1} \frac{x^{3} - 3x + 2}{x^{3} - x^{2} - x + 1} \]
is _________ (round off to one decimal place).
A thick cylinder has inner diameter 20 mm and outer diameter 40 mm, subjected to internal pressure of 100 MPa. Tensile stress is positive and compressive stress negative. The sum of radial and hoop stresses (in MPa) at radius 15 mm is ________ (round off to two decimal places).
A shaft is used to transmit a power of 10 kW. The shear yield stress of the material is 150 MPa and factor of safety is 2. The shaft rotates at 1440 revolutions per minute. The diameter of the shaft (in mm) based on static strength is ________. [round off to two decimal places]
Air at an initial temperature and pressure of 15 °C and 1 bar is heated in an irreversible process. The final temperature and pressure are 303 °C and 2 bar, respectively. Take gas constant \(R = 287\) J/kg·K, \(\gamma = 1.4\), and treat air as a calorically perfect gas. The change of entropy (in J/kg·K) in the process is ______. [round off to nearest integer]
During a hot-working process, the homologous temperature is 0.8. The melting point of the work metal is 800\(^\circ\)C. The temperature (in \(^\circ\)C) during hot-working is ________ (round off to nearest integer).
A workpiece of 30 mm diameter and 40 mm height is compressed between two platens in an open-die forging process. Assume a perfectly plastic material with a flow stress of 300 MPa. The ideal forging load (in kN) at 30% reduction is ________ (round off to nearest integer).
In a gas tungsten arc welding process under steady state condition, the input voltage and current are measured as 18 V and 160 A, respectively. Heat loss during creation of arc is 40% of the input power. Heat loss through convection and radiation from the workpiece is 800 W. The effective power (in W) utilized to melt the workpiece is ________. [round off to nearest integer]
During straight turning of a 20 mm diameter steel bar at a spindle speed of 400 RPM with an HSS tool, a tool life of 10 minutes was observed. When the same bar was turned at 200 RPM, the tool life increased to 40 minutes. The tool life (in minute) while machining the bar at 300 RPM is ________. [round off to nearest integer]
A cylindrical workpiece is turned using two different tools. Tool 1 has zero nose radius; the side and end cutting edge angles are \(20^\circ\) and \(10^\circ\), respectively. Tool 2 has a 0.5 mm nose radius. Both tools machine at a feed of \(0.2\ mm/rev\). The ratio of the \emph{ideal maximum height of unevenness on the surface produced by Tool 1 to that produced by Tool 2 is _________ (round off to one decimal place).
For an electrochemical machining process \[ \frac{dy}{dt}=\frac{\lambda}{y}-f , \]
where \(y\) is the inter-electrode gap in mm at time \(t\) (in minute), and \(f\) is the feed of the tool in mm/minute. The value of \(\lambda\) is \(6\times10^{-3}\) cm\(^{2}\)/minute. For maintaining a constant inter-electrode gap of 0.1 mm, the feed (in mm/minute) should be ________. [round off to one decimal place]
The worktable of an open loop positioning system is driven by a lead screw with a pitch of 4 mm. The lead screw is connected to the shaft of a stepper motor. A gear of 80 teeth mounted on the stepper motor shaft meshes with a gear of 20 teeth mounted on the lead screw. The step angle of the stepper motor is \(9^\circ\). The number of pulses required to move the table by 200 mm is ________. [in integer]
The diameter of a cylindrical cavity is measured using two spherical steel balls of diameters 3 cm and 4 cm. The balls are placed inside the cavity such that the bigger ball is above the smaller one as shown. If the cavity depth is 6 cm, the cavity diameter (in cm) is ________ (round off to two decimal places).

Five samples of size 80 are inspected. A p-chart with ±3σ limits is used. The defective counts are 4, 10, 5, 6, and 5. The upper control limit (fraction defective) is ________ (round off to two decimal places).

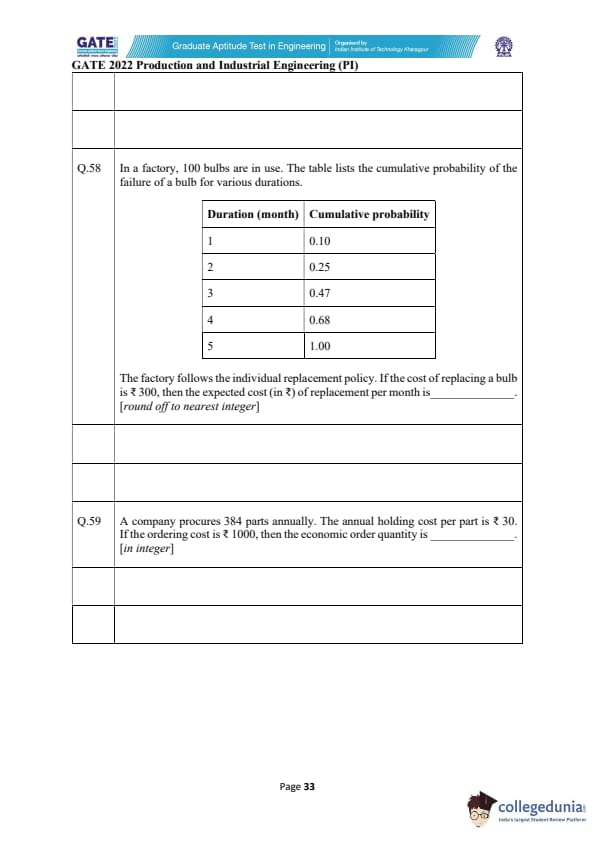
In a factory, 100 bulbs are in use. The table lists the cumulative probability of the failure of a bulb for various durations.

The factory follows the individual replacement policy. If the cost of replacing a bulb is ₹300, then the expected cost (in ₹) of replacement per month is ________. [round off to nearest integer]
A company procures 384 parts annually. The annual holding cost per part is ₹30. If the ordering cost is ₹1000, then the economic order quantity is _______. [in integer]
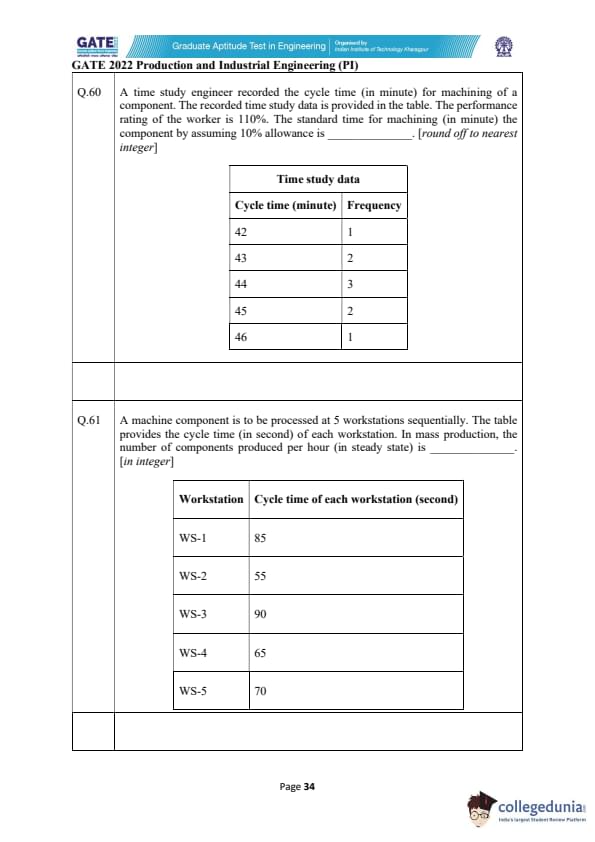
A time study engineer recorded the cycle time (in minute) for machining of a component. The recorded time study data is given below. The performance rating of the worker is 110%. The standard time (in minute) by assuming 10% allowance is ________. [round off to nearest integer]

A machine component is processed at 5 workstations sequentially. The cycle time (in seconds) for each workstation is given. In mass production, the number of components produced per hour (steady state) is _______. [in integer]

A vaccine has to be distributed from two warehouses (W1 and W2) to three hospitals (H1, H2, H3). Supplies at W1 and W2 are 200 and 150. Demands at H1, H2, H3 are 100, 150 and 125. Transportation cost (₹ per vaccine) is shown below. Using the Northwest-Corner method, the total transportation cost (₹) is ________ (round off to nearest integer).

Given LP: Max \(z = 20x_1 + 6x_2 + Px_3\), subject to: \(8x_1 + 2x_2 + 3x_3 \le 250\), \(4x_1 + 3x_2 \le 150\), \(2x_1 + x_3 \le 50\), \(x_1,x_2,x_3 \ge 0.\)
Optimal solution: \(x_1^=0,\;x_2^=50,\;x_3^=50.\)
Optimal dual variables: \(y_1^=0,\;y_2^=2,\;y_3^=8.\)
Find the value of parameter \(P\) such that the solution remains optimal (round off to one decimal place).
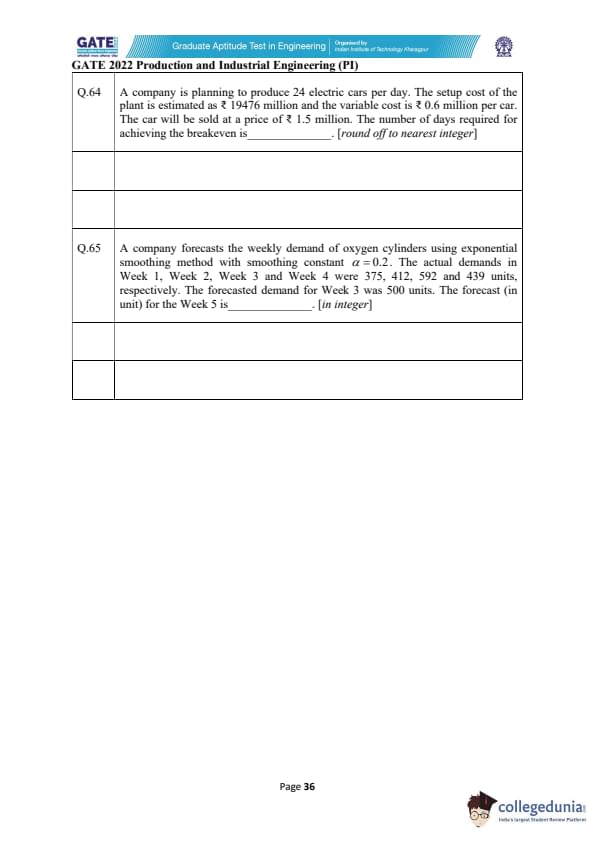
A company is planning to produce 24 electric cars per day. The setup cost of the plant is estimated as ₹ 19476 million and the variable cost is ₹ 0.6 million per car. The car will be sold at a price of ₹ 1.5 million. The number of days required for achieving the breakeven is _______. [round off to nearest integer]
A company forecasts the weekly demand of oxygen cylinders using exponential smoothing with smoothing constant \(\alpha = 0.2\). The actual demands in Week 1 to Week 4 were 375, 412, 592 and 439 units. The forecast for Week 3 was 500 units. The forecast (in unit) for Week 5 is ______. [in integer]





























GATE Previous Year Question Papers
| GATE 2023 Question Papers | GATE 2022 Question Papers | GATE 2021 Question Papers |
| GATE 2020 Question Papers | GATE 2019 Question Papers | GATE 2018 Question Papers |
Also Check:





Comments