GATE 2022 Naval Architecture and Marine Engineering (NM) Question Paper with Solutions PDFs can be downloaded from this page. IIT Kharagpur successfully concluded GATE 2022 NM on 6th February, 2022 in the Forenoon Session (9:00 AM to 12:00 PM). As per the test-takers, the overall difficulty level of GATE 2022 was measured as difficult. GATE 2022 NM question paper comprised 65 questions (10 General Aptitude questions, while rest of the 55 questions were related to core NM). The General Aptitude section was rated moderate, while the subject specific questions were of moderate difficulty.
GATE 2022 Naval Architecture and Marine Engineering (NM) Question Paper with Solutions
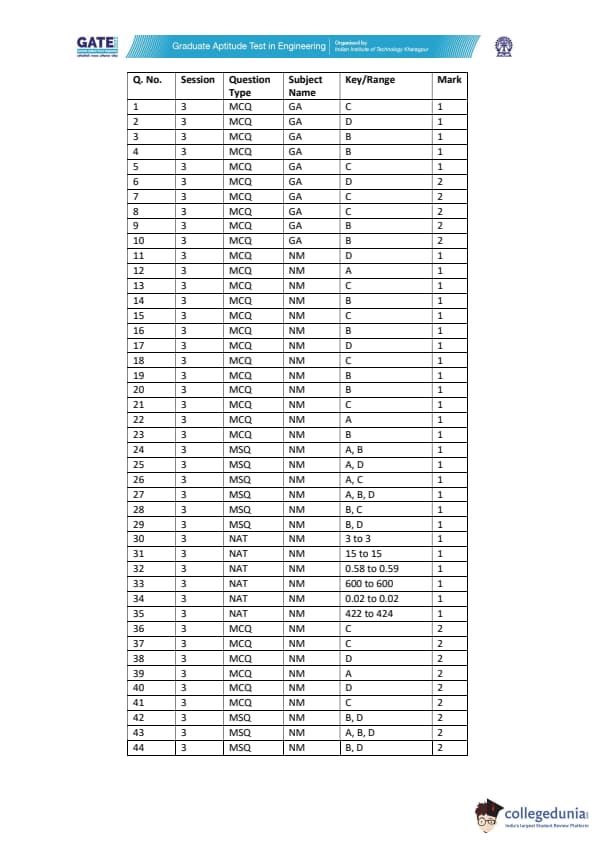
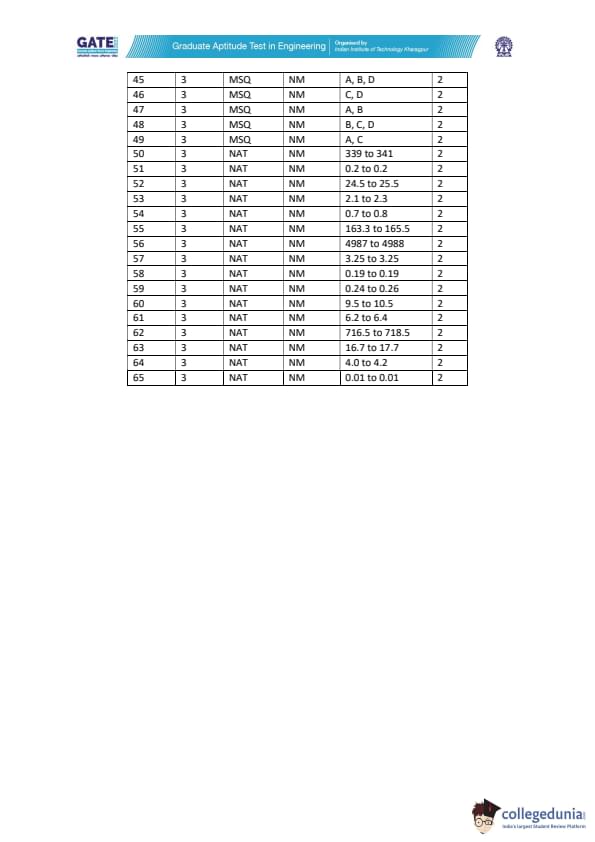
| GATE 2022 Naval Architecture and Marine Engineering (NM) Question Paper | Check Solutions |

Mr. X speaks _____ Japanese _____ Chinese.
A sum of money is to be distributed among P, Q, R, and S in the proportion 5 : 2 : 4 : 3, respectively.
If R gets ₹1000 more than S, what is the share of Q (in ₹)?
A trapezium has vertices marked as P, Q, R, and S (in that order anticlockwise). The side PQ is parallel to side SR. Further, it is given that, PQ = 11 cm, QR = 4 cm, RS = 6 cm, and SP = 3 cm. What is the shortest distance between PQ and SR (in cm)?
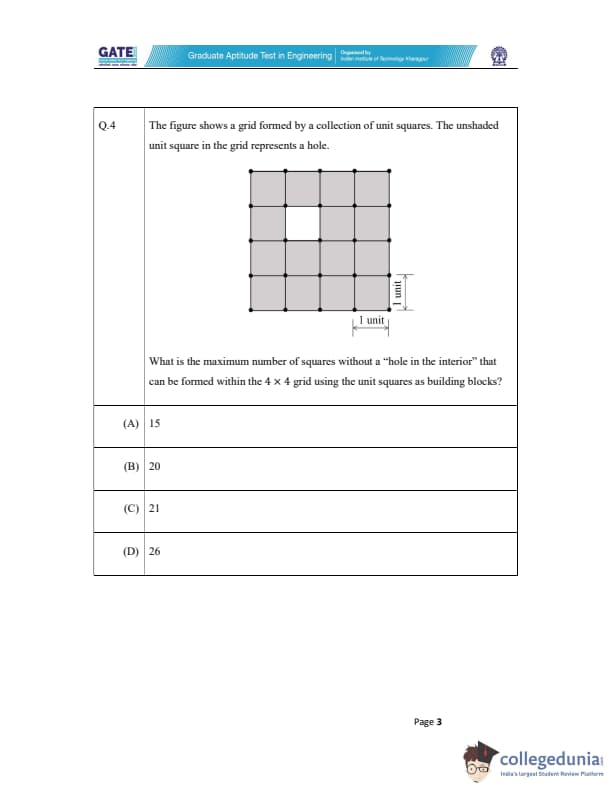
The figure shows a grid formed by a collection of unit squares. The unshaded unit square in the grid represents a hole. What is the maximum number of squares without a "hole in the interior" that can be formed within the 4 \(\times\) 4 grid using the unit squares as building blocks?

An art gallery engages a security guard to ensure that the items displayed are protected. The diagram below represents the plan of the gallery where the boundary walls are opaque. The location the security guard posted is identified such that all the inner space (shaded region in the plan) of the gallery is within the line of sight of the security guard.
If the security guard does not move around the posted location and has a 360° view, which one of the following correctly represents the set of ALL possible locations among the locations P, Q, R and S, where the security guard can be posted to watch over the entire inner space of the gallery?

Mosquitoes pose a threat to human health. Controlling mosquitoes using chemicals may have undesired consequences. In Florida, authorities have used genetically modified mosquitoes to control the overall mosquito population. It remains to be seen if this novel approach has unforeseen consequences.
Which one of the following is the correct logical inference based on the information in the above passage?
Consider the following inequalities.
(i) 2x - 1 \(>\) 7
(ii) 2x - 9 \(<\)1
Which one of the following expressions below satisfies the above two inequalities?
Four points \( P(0, 1), Q(0, -3), R(-2, -1), \) and \( S(2, -1) \) represent the vertices of a quadrilateral. What is the area enclosed by the quadrilateral?
In a class of five students P, Q, R, S and T, only one student is known to have copied in the exam. The disciplinary committee has investigated the situation and recorded the statements from the students as given below.
Statement of P: R has copied in the exam.
Statement of Q: S has copied in the exam.
Statement of R: P did not copy in the exam.
Statement of S: Only one of us is telling the truth.
Statement of T: R is telling the truth.
The investigating team had authentic information that S never lies.
Based on the information given above, the person who has copied in the exam is:
Consider the following square with the four corners and the center marked as P, Q, R, S and T respectively.
Let X, Y, and Z represent the following operations:
X: rotation of the square by 180 degree with respect to the S-Q axis.
Y: rotation of the square by 180 degree with respect to the P-R axis.
Z: rotation of the square by 90 degree clockwise with respect to the axis perpendicular, going into the screen and passing through the point T.
Consider the following three distinct sequences of operation (which are applied in the left to right order).

(1) XYZ
(2) XY
(3) ZZZZ
Which one of the following statements is correct as per the information provided above?
Let \( A \) be a real non-zero square matrix of order \( n \). If the homogeneous system of linear equations \( Ax = 0 \) has only the trivial solution, then:
Let \( z = x + iy \), where \( x \) and \( y \) are real numbers. Consider the complex functions: \[ f(z) = (x^2 - y^2) + i 2xy \]
and \[ g(z) = 2xy + i(x^2 - y^2) \]
Then on the complex plane,
If a population has exponential distribution with mean 1, then its median is:
Let \( \omega_f \) be the excitation frequency of a sinusoidal load and \( \omega_n \) be the natural frequency of a single degree of freedom system. Then the dynamic response of the system is highly affected by the stiffness of the system when:
A truck loaded with a half-filled water tank is moving at a constant horizontal acceleration \(a\). The acceleration due to gravity is \(g\). At steady state, the angle \(\theta\) made by the free surface with the horizontal plane is
Which one of the following combinations of elementary flows will lead to an ideal flow past a deeply submerged circular cylinder with circulation?
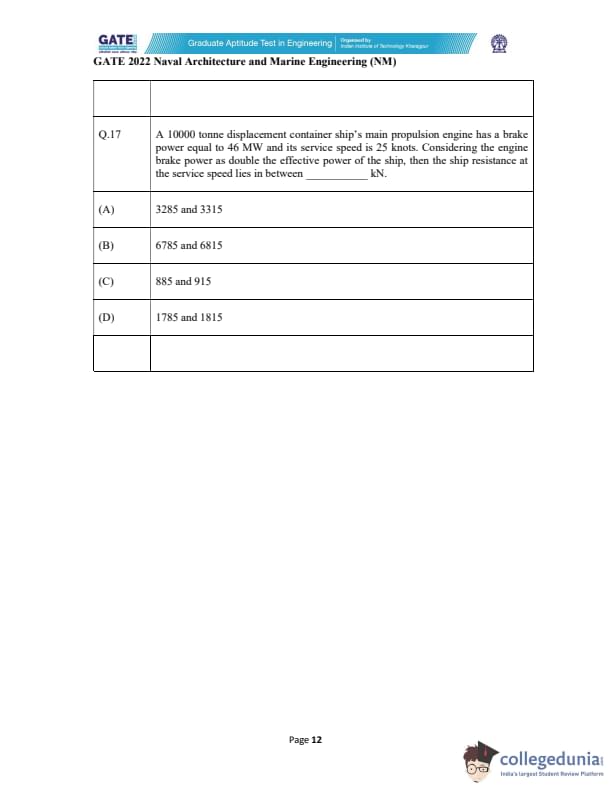
A 10000 tonne displacement container ship’s main propulsion engine has a brake power equal to 46 MW and its service speed is 25 knots. Considering the engine brake power as double the effective power of the ship, then the ship resistance at the service speed lies in between __________ kN.
The margin line used for the floodable length calculation of a ship is:
Consider a rectangular box barge of length 80 m, breadth 20 m and depth 15 m floating at an even draught of 10 m. Assume that the heave added mass of the vessel is equal to its mass displacement and the acceleration due to gravity is 9.81 m/s\(^2\). The heave natural period of the vessel lies in between ________ s.
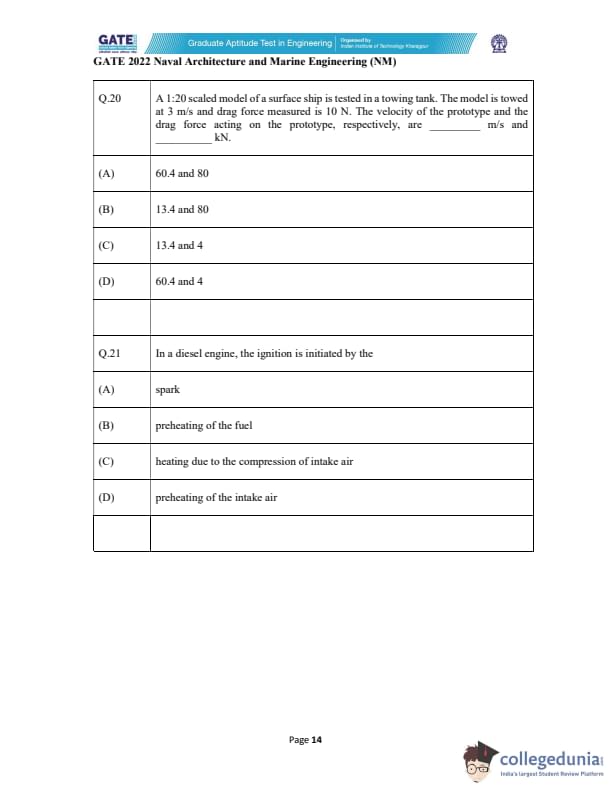
A 1:20 scaled model of a surface ship is tested in a towing tank. The model is towed at 3 m/s and drag force measured is 10 N. The velocity of the prototype and the drag force acting on the prototype, respectively, are ________ m/s and ________ kN.
In a diesel engine, the ignition is initiated by the:
In an internal combustion engine, supercharging is the process of supplying intake air at a pressure
The most desirable property amongst the following for a lubricating oil is:
If \(\dfrac{a_0}{2} + \sum_{n=1}^{\infty} a_n \cos(nx)\) is the Fourier cosine series of the function \(f(x)=\sin x,\; 0
A simply supported beam is loaded with a uniformly distributed load (UDL). Which statements about strain energy are TRUE?
Which of the following flows are represented by the velocity field, \[ \mathbf{V} = (x^2 - y^2) \hat{i} - 2xy \hat{j}? \]
If a ship enters shallow water from deep water, maintaining the same speed, then which of the following are TRUE?
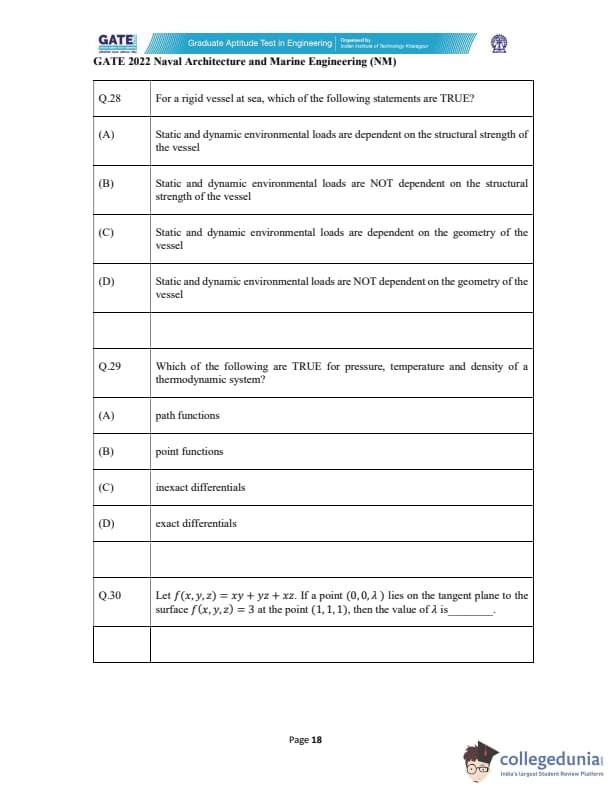
For a rigid vessel at sea, which of the following statements are TRUE?
Which of the following are TRUE for pressure, temperature and density of a thermodynamic system?
Let \( f(x,y,z)=xy+yz+xz \). If a point \( (0,0,\lambda) \) lies on the tangent plane to the surface \( f(x,y,z)=3 \) at the point \( (1,1,1) \), then the value of \( \lambda \) is _____.
The beam fixed at end A and simply supported at C with a roller is shown in the figure. If B is an internal hinge and a 10 kN point load acts at D, and a UDL of 10 kN/m acts on AB, the magnitude of bending moment at the fixed end A is ______ kNm.

The laminar and turbulent boundary layer thickness of a flat plate are: \[ \delta_l = \frac{5x}{Re_x^{1/2}}, \qquad \delta_t = \frac{0.37\,x}{Re_x^{1/5}} \]
The fluid has kinematic viscosity \( \nu = 10^{-6}\ m^2/s \). A 100 m long plate moves at 10 m/s. The boundary layer thickness at the rear end of the plate is ______ m (rounded to two decimals).
The diameter and rotating speed of a cargo ship propeller are 7.5 m and 120 RPM, respectively. An open water test is to be performed in a towing tank with a propeller model of 300 mm diameter. The corresponding propeller model speed is ________ RPM.
Assume that a ship has length \(L = 200 \, m\) and operates at a design speed \(U = 12 \, m/s\). If in a turning circle maneuver the ship exhibits a steady turning diameter of \(6L\), then the yaw rate of the ship is ________ rad/s (correct to two decimal places).
If the maximum static deflection of a shaft is 5 mm, then the estimated critical speed using Rayleigh–Ritz method is ______ RPM (rounded off to nearest integer).
The value of the line integral \[ \oint_{C} (-3y\,dx + 3x\,dy + z\,dz) \]
along the circle \( C: x^{2} + y^{2} = 1,\ z = 1 \) oriented in the clockwise sense as seen from the origin, is
A column of height 20 m is fixed at both ends. If Young’s modulus is \(E = 17\times 10^{9}\ N/m^2\)
and moment of inertia \(I = 3.255\times 10^{-4}\ m^4\),
then the first critical buckling load lies between ________ kN.
In a potential flow field, if the stream function \( \psi = xy^2 \), then the velocity potential \( \phi \) is:
For a container ship, the propeller open water efficiency, thrust deduction fraction, and wake fraction are 0.60, 0.19, and 0.25, respectively. If the relative rotative efficiency of the propeller is 1.0, then the hull efficiency and quasi-propulsive efficiency of the propeller, respectively, are:
Consider the wave elevation spectrum \(S_{\eta\eta}(\omega)\) as shown in the figure. Then, the significant wave height is ________ m.

If \(\Delta h_m\) and \(\Delta h_f\) are the enthalpy drops across the moving and fixed blades of a turbine stage, then the degree of reaction is
Let \[ M = \begin{pmatrix} 2 & -1 & 1
-1 & 2 & -1
1 & -1 & 2 \end{pmatrix} \]
Which of the following are TRUE?
Which of the following statements are TRUE about the assumptions adopted in Euler’s column theory?
An autonomous underwater vehicle is made of a long cylinder with a semi-ellipsoid at the forward end and a hemisphere at the aft end as shown in the figure. The origin of the reference frame is located at the centroid of the cylinder.
The positive x, y and z axes, respectively, are pointing towards forward, port and upward directions. The surge, sway and heave motions are represented by indices 1-2-3 and roll, pitch and yaw motions are represented by indices 4-5-6, respectively.
If A = [A\(_{ij}\)] is the added mass matrix, then which of the following are NOT zero?

If a ship hull is subdivided into different watertight compartments, which of the following statements are TRUE?
Consider the midship section of a vessel with the centerline (CL) and neutral axis (NA) as shown in the figure. Assume that the cross-section is symmetric about the centerline, the plate thickness is uniform throughout the section and \(h_1 < h_2\).
When the vessel is subjected to a vertical bending moment in its upright condition, which of the following statements are TRUE?

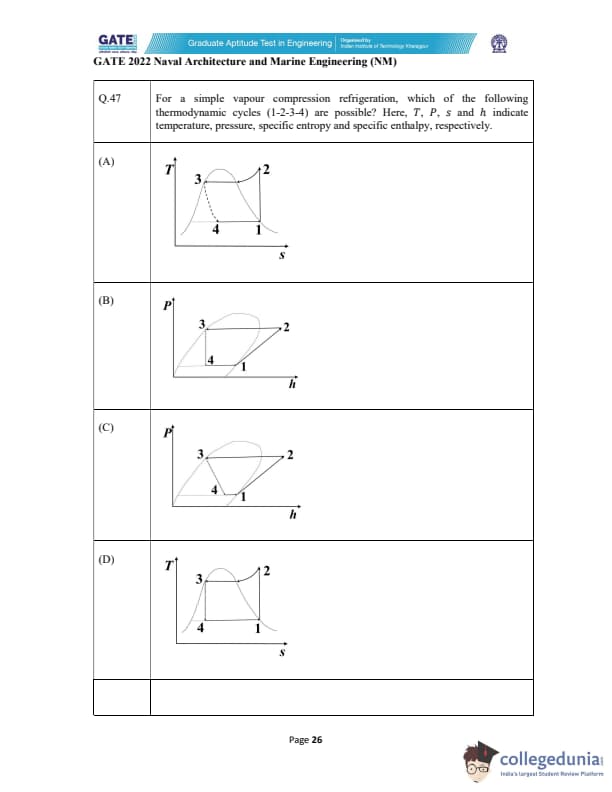
For a simple vapour compression refrigeration, which of the following thermodynamic cycles (1-2-3-4) are possible? Here, \( T \), \( P \), \( S \), and \( h \) indicate temperature, pressure, specific entropy, and specific enthalpy, respectively.

Which of the following statements are TRUE for a fluid flow over a deeply submerged body?
For an Otto cycle with compression ratio \(r\) and specific heat ratio \(\gamma\), which expression represents the thermal efficiency?
Let \(y(x)\) be the solution of the differential equation \(y'' - 4y' - 12y = 3e^{5x}\)
satisfying \(y(0)=\frac{18}{7}\) and \(y'(0)=-\frac{1}{7}\).
Then \(y(1)\) is _______ (rounded off to nearest integer).
We have two coins. One is biased with probability of head = 1.0 and the other is a fair coin.
One coin is chosen at random and tossed twice.
If both outcomes are heads, the probability that the chosen coin is fair is ______ (correct to one decimal place).
An element, as shown in the figure, is subjected to stresses \(\sigma_x = 500\ N/m^2\), \(\sigma_y = 300\ N/m^2\) and \(\tau = 120\ N/m^2\).
If \(\sigma_1\) and \(\sigma_2\) are the principal stresses, then the absolute value of the angle \(\varphi\) is ________ degree (rounded off to one decimal place).

An under-damped single-degree-of-freedom system is freely oscillating with an initial amplitude \(A\). The initial velocity is zero. After five cycles of oscillation, the amplitude reduces to \(A/2\).
Then the damping ratio of the system is ________ % (rounded off to one decimal place) of critical damping.
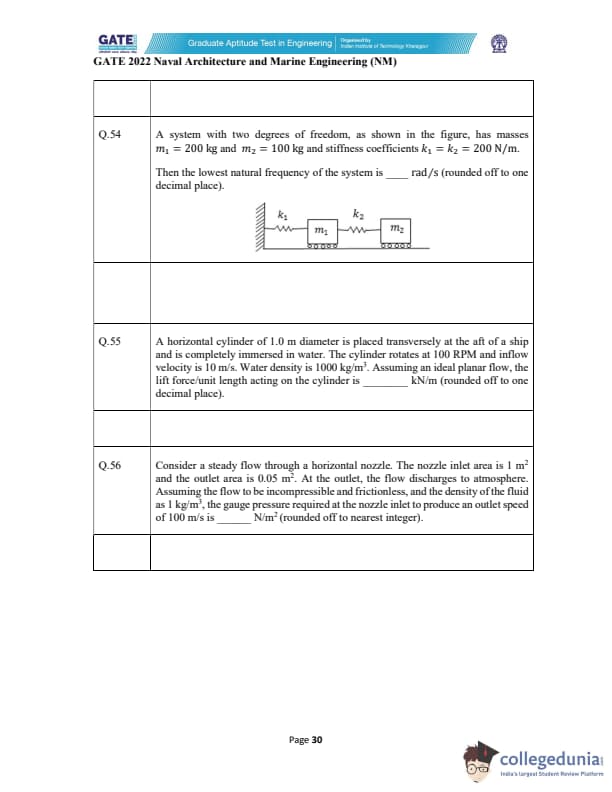
A system with two degrees of freedom, as shown in the figure, has masses \(m_1 = 200\ kg\) and \(m_2 = 100\ kg\) and stiffness coefficients \(k_1 = k_2 = 200\ N/m\).
Then the lowest natural frequency of the system is ______ rad/s (rounded off to one decimal place).

A horizontal cylinder of 1.0 m diameter is placed transversely at the aft of a ship and is completely immersed in water. The cylinder rotates at 100 RPM and inflow velocity is 10 m/s. Water density is 1000 kg/m\(^3\).
Assuming an ideal planar flow, the lift force per unit length acting on the cylinder is ______ kN/m (rounded off to one decimal place).
Consider a steady flow through a horizontal nozzle. The nozzle inlet area is 1 m\(^2\) and the outlet area is 0.05 m\(^2\). At the outlet, the flow discharges to atmosphere. Assuming the flow to be incompressible and frictionless, and the density of the fluid as 1 kg/m\(^3\), the gauge pressure required at the nozzle inlet to produce an outlet speed of 100 m/s is ________ N/m\(^2\) (rounded off to nearest integer).
A rectangular barge has length (L) of 100 m, breadth (B) of 18 m and depth (D) of 10 m. It is subdivided transversely into four equal compartments of equal length with the end compartments loaded fully with oil of density = 0.9 tonne/m\(^3\). The barge floats in water having a density of 1000 kg/m\(^3\). If the hull structural weight is ignored, then the transverse metacentric height of the barge is _______ m (correct to two decimal places).

A propeller rotating at a speed of 108 RPM behind the ship produces a thrust of 720 kN with a torque of 700 kNm, when it travels at a speed of 15 knots. In open water, this propeller rotating at the same speed, produces the same thrust at an advance speed of 12 knots, and develops the same torque at an advance speed of 12.3 knots. Then, the average of the wake fractions is ______ (correct to two decimal places).
Consider a point source in a uniform flow of velocity \(U = 4\) m/s along the positive \(x\)-axis as shown in the figure. Assume a two-dimensional steady potential flow. The potential due to the point source is given by \(\log_e(r)\), where \(r^2 = x^2 + y^2\).
Then the magnitude of the distance \(d\) between the point source and the stagnation point is ________ m (rounded off to two decimal places).

Consider a ship with one half of its midship cross-section with moulded breadth \(B = 30\ m\) and moulded depth \(D = 9\ m\). The deck, side-shell, and bottom plate have the same thickness. The yield stress of the material is \(240\ MPa\). The section is subjected to a vertical bending moment of \(712.8\ MN·m\). Ignore the self-moment of inertia of deck and bottom plating. The distance of the farthest fiber from the neutral axis is taken excluding plate thickness. If maximum bending stress equals yield stress, the required plate thickness is ______ mm (rounded off to one decimal place).

A ship moves at \(U = 9.81\ m/s\) in deep water. A wave is incident at an angle \(\beta = 120^\circ\). The encounter period measured onboard is \(4.187\ s\). Using \(g = 9.81\ m/s^2\), determine the actual wave period ______ s (rounded off to one decimal place).

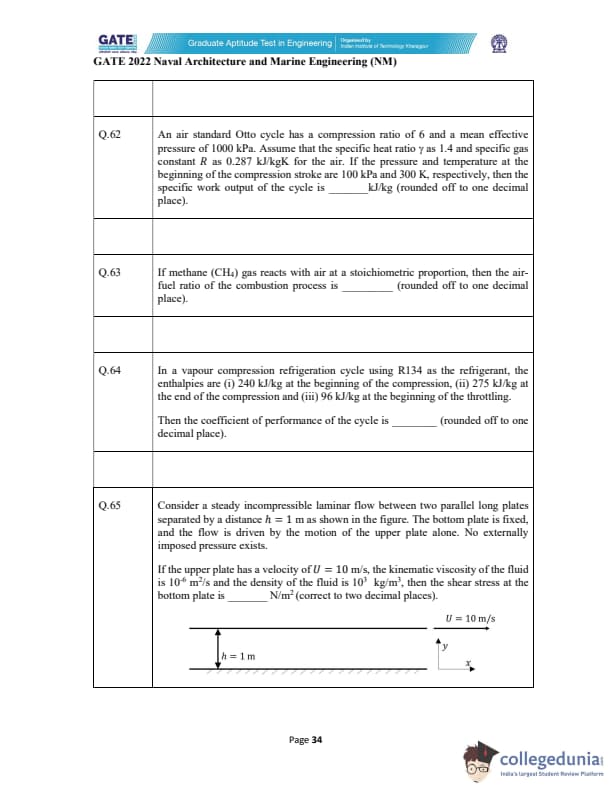
An air standard Otto cycle has a compression ratio of 6 and a mean effective pressure of 1000 kPa. Assume that the specific heat ratio \(\gamma\) is 1.4 and specific gas constant \(R\) as 0.287 kJ/kgK for the air. If the pressure and temperature at the beginning of the compression stroke are 100 kPa and 300 K, respectively, then the specific work output of the cycle is ________ kJ/kg (rounded off to one decimal place).
If methane (CH\(_4\)) gas reacts with air at a stoichiometric proportion, then the air–fuel ratio of the combustion process is ________ (rounded off to one decimal place).
In a vapour compression refrigeration cycle using R134a, the enthalpies are
(i) 240 kJ/kg at the beginning of compression,
(ii) 275 kJ/kg at the end of compression,
(iii) 96 kJ/kg at the beginning of throttling.
Then the coefficient of performance (COP) of the cycle is ______ (rounded off to one decimal place).
A steady incompressible laminar flow exists between two long parallel plates separated by \(h = 1\ m\).
The bottom plate is fixed and the upper plate moves with velocity \(U = 10\ m/s\).
The kinematic viscosity of the fluid is \(10^{-6}\ m^2/s\) and density is \(10^3\ kg/m^3\).
No pressure gradient acts.
Then the shear stress at the bottom plate is ______ N/m\(^2\) (correct to two decimal places).



























Quick Links:
GATE 2022 NM Detailed Paper Analysis
IIT Kharagpur listed MCQs (Multiple Choice Questions), MSQs (Multiple Select Questions), and NATs (Numerical Answer Type) questions, in the question paper of GATE 2022 NM. The below-mentioned table shows the details of MCQs, MSQs, and NATs that appeared in GATE NM question paper 2022:
| Question Types | Question Frequency | Carried Marks |
|---|---|---|
| No. Of 1 Mark MCQs | 18 | 18 |
| No. Of 2 Marks MCQs | 11 | 22 |
| No. Of 1 Mark NATs | 6 | 6 |
| No. Of 2 Marks NATs | 16 | 32 |
| No. Of 1 Mark MSQs | 6 | 6 |
| No. Of 2 Marks MSQs | 8 | 16 |
| Total | 65 | 100 |
- Topics such as Fluid Mechanics and Engineering Mathematics carried the highest weightage in the exam
- The other core NM topics includes Applied Mechanics and Structure, Naval Architecture and Ocean Engineering, Thermodynamics, and Marine Engineering
- An attempt of somewhere between 40-45 was considered a good attempt.
Also Check:
GATE Previous Year Question Papers:
| GATE 2022 Question Papers | GATE 2021 Question Papers | GATE 2020 Question Papers |
| GATE 2019 Question Papers | GATE 2018 Question Papers | GATE 2017 Question Papers |





Comments