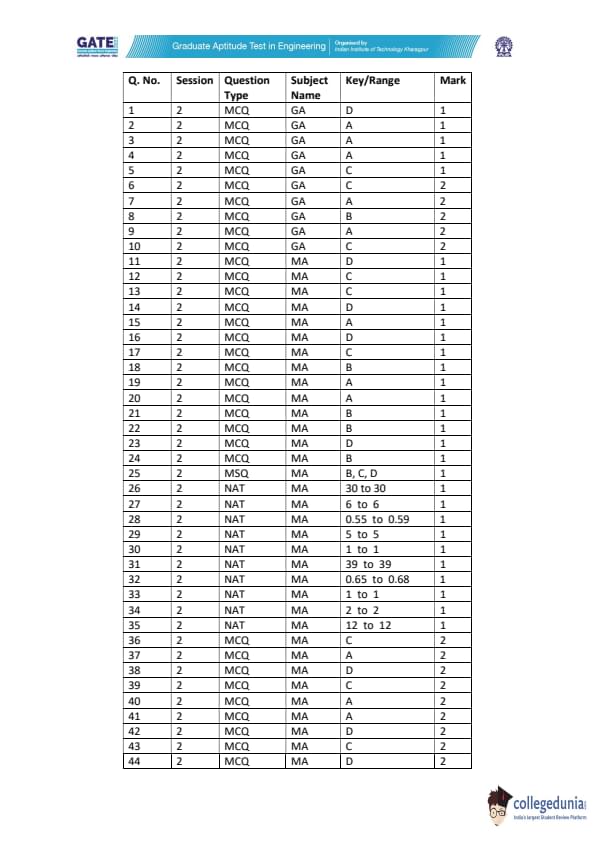
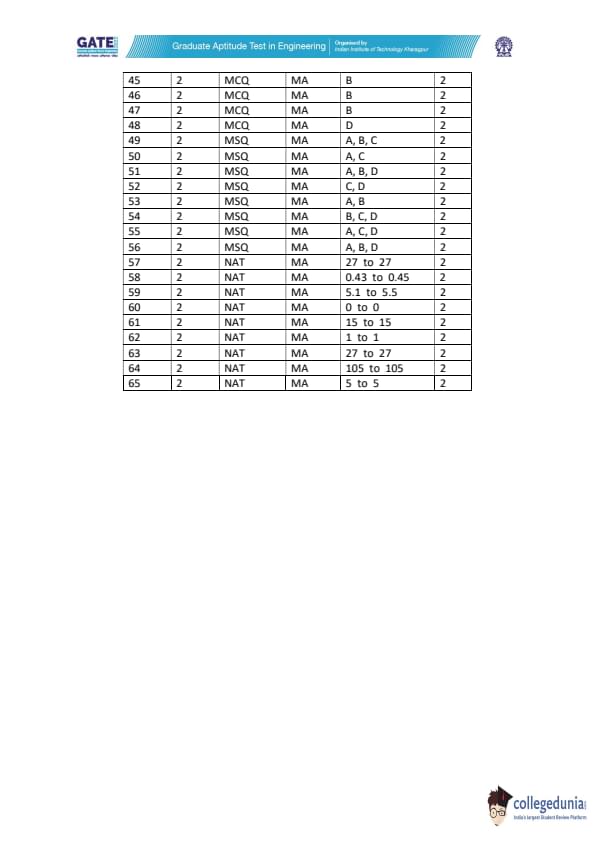
GATE 2022 Mathematics (MA) Question Paper with Solutions PDFs are available to download. GATE 2022 MA was held on 5th February, 2022 in the Afternoon Session (2:30 PM to 5:30 PM). The overall paper was rated easy to moderate in terms of difficulty level. Topics such as Topology, Real Analysis, and Calculus carried the highest weightage in GATE 2022 MA question paper. Algebra and Functional Analysis held the least weightage in the exam.
GATE 2022 Mathematics (MA) Question Paper with Solutions
| GATE 2022 Mathematics (MA) Question Paper | Check Solutions |

As you grow older, an injury to your \hspace{2cm} may take longer to \hspace{2cm}.
In a 500 m race, P and Q have speeds in the ratio of 3 : 4. Q starts the race when P has already covered 140 m.
What is the distance between P and Q (in m) when P wins the race?
Three bells P, Q, and R are rung periodically in a school. P is rung every 20 minutes; Q is rung every 30 minutes and R is rung every 50 minutes.
If all the three bells are rung at 12:00 PM, when will the three bells ring together again the next time?
Given below are two statements and four conclusions drawn based on the statements.
Statement 1: Some bottles are cups.
Statement 2: All cups are knives.
Conclusion I: Some bottles are knives.
Conclusion II: Some knives are cups.
Conclusion III: All cups are bottles.
Conclusion IV: All knives are cups.
Which one of the following options can be logically inferred?
The figure below shows the front and rear view of a disc, which is shaded with identical patterns. The disc is flipped once with respect to any one of the fixed axes 1-1, 2-2, or 3-3 chosen uniformly at random.
What is the probability that the disc DOES NOT retain the same front and rear views after the flipping operation?

Altruism is the human concern for the wellbeing of others. Altruism has been shown to be motivated more by social bonding, familiarity, and identification of belongingness to a group. The notion that altruism may be attributed to empathy or guilt has now been rejected.
Which one of the following is the CORRECT logical inference based on the information in the above passage?
There are two identical dice with a single letter on each of the faces. The following six letters: Q, R, S, T, U, and V, one on each of the faces. Any of the six outcomes are equally likely.
The two dice are thrown once independently at random.
What is the probability that the outcomes on the dice were composed only of any combination of the following possible outcomes: Q, U, and V?
The price of an item is 10% cheaper in an online store S compared to the price at another online store M. Store S charges ₹150 for delivery. There are no delivery charges for orders from store M. A person bought the item from the store S and saved ₹100.
What is the price of the item at the online store S (in ₹) if there are no other charges than what is described above?
The letters P, Q, R, S, T, and U are to be placed one per vertex on a regular convex hexagon, but not necessarily in the same order.
Consider the following statements:
The line segment joining R and S is longer than the line segment joining P and Q.
The line segment joining R and S is perpendicular to the line segment joining P and Q.
The line segment joining R and U is parallel to the line segment joining T and Q.
Based on the above statements, which one of the following options is CORRECT?
An ant is at the bottom-left corner of a grid (point P) as shown above. It aims to move to the top-right corner of the grid. The ant moves only along the lines marked in the grid such that the current distance to the top-right corner strictly decreases.
Which one of the following is part of a possible trajectory of the ant during the movement?


Suppose that the characteristic equation of \( M \in \mathbb{C}^{3 \times 3} \) is \[ \lambda^3 + \alpha \lambda^2 + \beta \lambda - 1 = 0, \]
where \( \alpha, \beta \in \mathbb{C} \) with \( \alpha + \beta \neq 0 \).
Which of the following statements is TRUE?
Consider
P: Let \( M \in \mathbb{R}^{m \times n} \) with \( m > n \geq 2 \). If \( rank(M) = n \), then the system of linear equations \( Mx = 0 \) has \( x = 0 \) as the only solution.
Q: Let \( E \in \mathbb{R}^{n \times n}, n \geq 2 \) be a non-zero matrix such that \( E^3 = 0 \). Then \( I + E^2 \) is a singular matrix.
Which of the following statements is TRUE?
Consider the real function of two real variables given by
\[ u(x, y) = e^{2x}[\sin 3x \cos 2y \cosh 3y - \cos 3x \sin 2y \sinh 3y]. \]
Let \( v(x, y) \) be the harmonic conjugate of \( u(x, y) \) such that \( v(0, 0) = 2 \). Let \( z = x + iy \) and \( f(z) = u(x, y) + iv(x, y) \), then the value of \( 4 + 2i f(i\pi) \) is
The value of the integral \[ \int_{C} \frac{z^{100}}{z^{101} + 1} \, dz \]
where C is the circle of radius 2 centered at the origin taken in the anti-clockwise direction is
Let \( X \) be a real normed linear space. Let \( X_0 = \{x \in X : \|x\| = 1\} \). If \( X_0 \) contains two distinct points \( x \) and \( y \) and the line segment joining them, then, which of the following statements is TRUE?
Let \( \{ e_k : k \in \mathbb{N} \} \) be an orthonormal basis for a Hilbert space \( H \).
Define \( f_k = e_k + e_{k+1}, k \in \mathbb{N} \) and \( g_j = \sum_{n=1^{j (-1)^{n+1 e_n, j \in \mathbb{N.
\text{Then \quad \sum_{k=1^{\infty | \langle g_j, f_k \rangle |^2 = \, ?
Consider \( \mathbb{R}^2 \) with the usual metric. Let \[ A = \{(x, y) \in \mathbb{R}^2 : x^2 + y^2 \leq 1\} \quad and \quad B = \{(x, y) \in \mathbb{R}^2 : (x - 2)^2 + y^2 \leq 1\}. \]
Let \( M = A \cup B \) and \( N = interior(A) \cup interior(B) \).
Then, which of the following statements is TRUE?
The real sequence generated by the iterative scheme
\[ x_n = \frac{x_{n-1}}{2} + \frac{1}{x_{n-1}}, \quad n \geq 1 \]
The initial value problem \[ \frac{dy}{dx} = \cos(xy), \quad x \in \mathbb{R}, \quad y(0) = y_0, \]
where \( y_0 \) is a real constant, has
If eigenfunctions corresponding to distinct eigenvalues \( \lambda \) of the Sturm-Liouville problem
\[ \frac{d^2y}{dx^2} - 3 \frac{dy}{dx} = \lambda y, \quad 0 < x < \pi,
y(0) = y(\pi) = 0 \]
are orthogonal with respect to the weight function \( w(x) \), then \( w(x) \) is
The steady state solution for the heat equation \[ \frac{\partial u}{\partial t} - \frac{\partial^2 u}{\partial x^2} = 0, \quad 0 < x < 2, \, t > 0, \]
with the initial condition \( u(x, 0) = 0, \, 0 < x < 2 \) and the boundary conditions \( u(0, t) = 1 \) and \( u(2, t) = 3, \, t > 0 \) at \( x = 1 \) is
Consider \( ([0, 1], T_1) \), where \( T_1 \) is the subspace topology induced by the Euclidean topology on \( \mathbb{R} \), and let \( T_2 \) be any topology on \( [0, 1] \). Consider the following statements:
P: If \( T_1 \) is a proper subset of \( T_2 \), then \( ([0, 1], T_2) \) is not compact.
Q: If \( T_2 \) is a proper subset of \( T_1 \), then \( ([0, 1], T_2) \) is not Hausdorff.
Then, which of the following statements is TRUE?
Let \( p : ([0, 1], T_1) \to \{(0, 1\}, T_2) \) be the quotient map, arising from the characteristic function on \( [\frac{1}{2}, 1] \), where \( T_1 \) is the subspace topology induced by the Euclidean topology on \( \mathbb{R} \). Which of the following statements is TRUE?
Set \( X_n := \mathbb{R} \) for each \( n \in \mathbb{N} \). Define \( Y := \prod_{n \in \mathbb{N}} X_n \). Endow \( Y \) with the product topology, where the topology on each \( X_n \) is the Euclidean topology. Consider the set \[ \Delta = \{ (x, x, x, \dots) \mid x \in \mathbb{R} \} \]
with the subspace topology induced from \( Y \). Which of the following statements is TRUE?
Consider the linear system of equations \( Ax = b \) with
\[ A = \begin{pmatrix} 3 & 1 & 1
1 & 4 & 1
2 & 0 & 3 \end{pmatrix}, \quad b = \begin{pmatrix} 2
3
4 \end{pmatrix}. \]
Which of the following statements are TRUE?
The number of non-isomorphic abelian groups of order \(2^2 \cdot 3^3 \cdot 5^4\) is __________.
The number of subgroups of a cyclic group of order 12 is __________.
The radius of convergence of the series \[ \sum_{n \geq 0} 3^{n+1} z^{2n}, \quad z \in \mathbb{C} \]
is __________ (round off to TWO decimal places).
The number of zeros of the polynomial
\[ 2z^7 - 7z^5 + 2z^3 - z + 1 \]
in the unit disc \( \{ z \in \mathbb{C} : |z| < 1 \} \) is __________.
If \( P(x) \) is a polynomial of degree 5 and \[ \alpha = \sum_{i=0}^{6} P(x_i) \left( \prod_{\substack{j=0
j\neq i}}^{6} (x_i - x_j)^{-1} \right), \]
where \( x_0, x_1, \ldots, x_6 \) are distinct points in the interval \([2,3]\), then the value of \( \alpha^2 - \alpha + 1 \) is __________.
The maximum value of \( f(x, y) = 49 - x^2 - y^2 \) on the line \( x + 3y = 10 \) is __________.
If the function \( f(x, y) = x^2 + xy + y^2 + \frac{1}{x} + \frac{1}{y} \), \( x \neq 0, y \neq 0 \) attains its local minimum value at the point \( (a, b) \), then the value of \( a^3 + b^3 \) is __________ (round off to TWO decimal places).
If the ordinary differential equation
\[ x^2 \frac{d^2 \phi}{dx^2} + x \frac{d\phi}{dx} + x^2 \phi = 0, \quad x > 0 \]
has a solution of the form \( \phi(x) = x^r \sum_{n=0}^{\infty} a_n x^n \), where \( a_n \)'s are constants and \( a_0 \neq 0 \), then the value of \( r^2 + 1 \) is __________.
The Bessel functions \( J_\alpha(x), x > 0, \alpha \in \mathbb{R} \) satisfy \[ J_{\alpha-1}(x) + J_{\alpha+1}(x) = \frac{2\alpha}{x} J_\alpha(x). \]
Then, the value of \( \left( \pi J_{\frac{3}{2}}(\pi) \right)^2 \) is __________.
Let \( \mathbb{R}[X] \) denote the ring of polynomials in \( X \) with real coefficients. Then, the quotient ring \( \mathbb{R}[X]/(X^4 + 4) \) is
Consider the following conditions on two proper non-zero ideals \( J_1 \) and \( J_2 \) of a non-zero commutative ring \( R \):
P: For any \( r_1, r_2 \in R \), there exists a unique \( r \in R \) such that \( r - r_1 \in J_1 \) and \( r - r_2 \in J_2 \).
Q: \( J_1 + J_2 = R \)
Then, which of the following statements is TRUE?
Let \( f : [-\pi, \pi] \to \mathbb{R} \) be a continuous function such that \( f(x) > \frac{f(0)}{2} \) for \( |x| < \delta \), where \( 0 < \delta < \pi \). Define \( P_{n,\delta}(x) = (1 + \cos x - \cos \delta)^n \), for \( n = 1, 2, 3, \dots \). Then, which of the following statements is TRUE?
P: Suppose that \[ \sum_{n=0}^{\infty} a_n x^n converges at x = -3 and diverges at x = 6. Then \sum_{n=0}^{\infty} (-1)^n a_n converges. \]
Q: The interval of convergence of the series \[ \sum_{n=2}^{\infty} \frac{(-1)^n x^n}{4^n \log_e n} is [-4, 4]. \]
Which of the following statements is TRUE?
Let \[ f_n(x) = \frac{x^2}{x^2 + (1 - nx)^2}, \quad x \in [0, 1], \, n = 1, 2, 3, \dots. \]
Then, which of the following statements is TRUE?
Let \( (\mathbb{Q}, d) \) be the metric space with \[ d(x, y) = |x - y|. \]
Let \( E = \{ p \in \mathbb{Q} : 2 < p^2 < 3 \}. \)
Then, the set \( E \) is
Let \( T : L^2[-1, 1] \to L^2[-1, 1] \) be defined by \( T f = \tilde{f} \), where \( \tilde{f}(x) = f(-x) \) almost everywhere. If \( M \) is the kernel of \( I - T \), then the distance between the function \( \varphi(t) = e^t \) and \( M \) is
The first derivative of a function \( f \in C^\infty(-3, 3) \) is approximated by an interpolating polynomial of degree 2, using the data \[ (-1, f(-1)), (0, f(0)) and (2, f(2)). \]
It is found that \[ f'(0) \approx -\frac{2}{3} f(-1) + \alpha f(0) + \beta f(2). \]
Then, the value of \( \frac{1}{\alpha \beta} \) is
The first derivative of a function \( f \in C^\infty(-3, 3) \) is approximated by an interpolating polynomial of degree 2, using the data \[ (-1, f(-1)), (0, f(0)) and (2, f(2)). \]
It is found that \[ f'(0) \approx -\frac{2}{3} f(-1) + \alpha f(0) + \beta f(2). \]
Then, the value of \( \frac{1}{\alpha \beta} \) is
The work done by the force \( \mathbf{F} = (x + y) \hat{i} - (x^2 + y^2) \hat{j} \),
where \( \hat{i} \) and \( \hat{j} \) are unit vectors in \( \mathbf{O X} \) and \( \mathbf{O Y} \) directions, respectively, along the upper half of the circle \( x^2 + y^2 = 1 \) from \( (1, 0) \) to \( (-1, 0) \) in the \( xy \)-plane is
Let \( u(x, t) \) be the solution of the wave equation \[ \frac{\partial^2 u}{\partial t^2} = \frac{\partial^2 u}{\partial x^2}, \quad 0 < x < \pi, \, t > 0, \]
with the initial conditions \[ u(x, 0) = \sin x + \sin 2x + \sin 3x, \quad \frac{\partial u}{\partial t}(x, 0) = 0, \quad 0 < x < \pi, \]
and the boundary conditions \[ u(0, t) = u(\pi, t) = 0, \quad t \geq 0. \]
Then, the value of \( u \left( \frac{\pi}{2}, \pi \right) \) is
Let \( T : \mathbb{R}^2 \to \mathbb{R}^2 \) be a linear transformation defined by \[ T((1, 2)) = (1, 0) \quad and \quad T((2, 1)) = (1, 1). \]
For \( p, q \in \mathbb{R} \), let \( T^{-1}((p, q)) = (x, y) \).
Which of the following statements is TRUE?
Let \( y = (\alpha, -1)^T \), where \( \alpha \in \mathbb{R} \), be a feasible solution for the dual problem of the linear programming problem
Maximize: \( 5x_1 + 12x_2 \)
subject to: \[ x_1 + 2x_2 + x_3 \leq 10 \] \[ 2x_1 - x_2 + 3x_3 = 8 \] \[ x_1, x_2, x_3 \geq 0 \]
Which of the following statements is TRUE?
Let \( K \) denote the subset of \( \mathbb{C} \) consisting of elements algebraic over \( \mathbb{Q} \). Then, which of the following statements are TRUE?
Let \( T \) be a Möbius transformation such that \( T(0) = \alpha, T(\alpha) = 0 \) and \( T(\infty) = -\alpha \), where \( \alpha = \frac{-1 + i}{\sqrt{2}} \). Let \( L \) denote the straight line passing through the origin with slope \( -1 \), and let \( C \) denote the circle of unit radius centered at the origin. Then, which of the following statements are TRUE?
Let \( a > 0 \). Define \( D_a : L^2(\mathbb{R}) \to L^2(\mathbb{R}) \) by \[ (D_a f)(x) = \frac{1}{\sqrt{a}} f\left( \frac{x}{a} \right), almost everywhere, for f \in L^2(\mathbb{R}). \]
Then, which of the following statements are TRUE?
Let \( \{ \varphi_0, \varphi_1, \varphi_2, \dots \} \) be an orthonormal set in \( L^2[-1, 1] \) such that \( \varphi_n = C_n P_n \), where \( C_n \) is a constant and \( P_n \) is the Legendre polynomial of degree \( n \), for each \( n \in \mathbb{N} \setminus \{0\} \). Then, which of the following statements are TRUE?
Let \( X = (\mathbb{R}, T) \), where \( T \) is the smallest topology on \( \mathbb{R} \) in which all the singleton sets are closed. Then, which of the following statements are TRUE?
Consider \( (\mathbb{Z}, T) \), where \( T \) is the topology generated by sets of the form \[ A_{m,n} = \{ m + nk \mid k \in \mathbb{Z} \}, \quad for m, n \in \mathbb{Z} and n \neq 0. \]
Then, which of the following statements are TRUE?
Let \( A \in \mathbb{R}^{m \times n}, c \in \mathbb{R}^n \) and \( b \in \mathbb{R}^m \). Consider the linear programming primal problem
\[ Minimize: c^T x \] \[ subject to: A x = b, \quad x \geq 0. \]
Let \( x^0 \) and \( y^0 \) be feasible solutions of the primal and its dual, respectively. Which of the following statements are TRUE?
Consider \( \mathbb{R}^3 \) as a vector space with the usual operations of vector addition and scalar multiplication. Let \( x \in \mathbb{R}^3 \) be denoted by \( x = (x_1, x_2, x_3) \). Define subspaces \( W_1 \) and \( W_2 \) by \[ W_1 := \{ x \in \mathbb{R}^3 : x_1 + 2x_2 - x_3 = 0 \} \] \[ W_2 := \{ x \in \mathbb{R}^3 : 2x_1 + 3x_3 = 0 \}. \]
Let \( dim(U) \) denote the dimension of the subspace \( U \). Which of the following statements are TRUE?
Three companies \( C_1, C_2 \) and \( C_3 \) submit bids for three jobs \( J_1, J_2 \) and \( J_3 \). The costs involved per unit are given in the table below:

Then, the cost of the optimal assignment is __________.
The initial value problem \[ \frac{dy}{dx} = f(x, y), \quad y(x_0) = y_0 \]
is solved by using the following second-order Runge-Kutta method: \[ K_1 = h f(x_i, y_i) \] \[ K_2 = h f(x_i + \alpha h, y_i + \beta K_1) \] \[ y_{i+1} = y_i + \frac{1}{4} (K_1 + 3 K_2), \quad i \geq 0 \]
where \( h \) is the uniform step length between the points \( x_0, x_1, \dots, x_n \) and \( y_i = y(x_i) \). The value of the product \( \alpha \beta \) is __________ (round off to TWO decimal places).
The surface area of the paraboloid \( z = x^2 + y^2 \) between the planes \( z = 0 \) and \( z = 1 \) is __________ (round off to ONE decimal place).
The rate of change of \( f(x, y, z) = x + x \cos z - y \sin z + y \) at \( P_0(2, -1, 0) \) in the direction from \( P_0(2, -1, 0) \) to \( P_1(0, 1, 2) \) is __________.
If the Laplace equation \[ \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0, \quad 1 < x < 2, \quad 1 < y < 2 \]
with the boundary conditions \[ \frac{\partial u}{\partial x}(1, y) = y, \quad \frac{\partial u}{\partial x}(2, y) = 5, \quad 1 < y < 2 \]
and \[ \frac{\partial u}{\partial y}(x, 1) = \frac{\alpha x^2}{7}, \quad \frac{\partial u}{\partial y}(x, 2) = x, \quad 1 < x < 2 \]
has a solution, then the constant \( \alpha \) is __________.
Let \( u(x, y) \) be the solution of the first order partial differential equation \[ x \frac{\partial u}{\partial x} + (x^2 + y) \frac{\partial u}{\partial y} = u, \quad for all \, x, y \in \mathbb{R} \]
satisfying \( u(2, y) = y - 4 \), \( y \in \mathbb{R} \). Then, the value of \( u(1, 2) \) is __________.
The optimal value for the linear programming problem
Maximize: \( 6x_1 + 5x_2 \)
subject to: \[ 3x_1 + 2x_2 \leq 12 \] \[ -x_1 + x_2 \leq 1 \] \[ x_1, x_2 \geq 0 \]
is __________.
A certain product is manufactured by plants \( P_1, P_2 \) and \( P_3 \) whose capacities are 15, 25 and 10 units, respectively. The product is shipped to markets \( M_1, M_2, M_3 \) and \( M_4 \), whose requirements are 10, 10, 10 and 20, respectively. The transportation costs per unit are given in the table below.

Then the cost corresponding to the starting basic solution by the Northwest-corner method is __________.
Let \( M \) be a \( 3 \times 3 \) real matrix such that \( M^2 = 2M + 3I \). If the determinant of \( M \) is \( -9 \), then the trace of \( M \) equals _______ .


































































Quick Links:
GATE 2022 MA Detailed Paper Analysis
There were no changes in the overall exam pattern of GATE 2022 MA. A total of 65 questions constituted GATE 2022 MA Question Paper. Go through the below-mentioned table in order to get the details of the questions as per the carried marks-
| Question Types | Question Frequency | Carried Marks |
|---|---|---|
| No. Of 1 Mark MCQs | 19 | 19 |
| No. Of 2 Marks MCQs | 18 | 36 |
| No. Of 1 Mark NATs | 10 | 10 |
| No. Of 2 Marks NATs | 9 | 18 |
| No. Of 1 Mark MSQs | 1 | 1 |
| No. Of 2 Marks MSQs | 8 | 16 |
| Total | 65 | 100 |
- MCQs (Multiple Choice Questions) carried the maximum weightage in the exam
- There were a total of 9 MSQs (Multiple Select Questions) in the exam. 8 MSQs carried 2 marks, while only 1 MSQ carried 1 mark
- 19 out of 65 questions were NAT (Numerical Answer Type) questions.
- An attempt of 45+ questions was considered good for scoring a decent score in the examination.
Also Check:
GATE Previous Year Question Papers
| GATE 2023 Question Papers | GATE 2022 Question Papers | GATE 2021 Question Papers |
| GATE 2020 Question Papers | GATE 2019 Question Papers | GATE 2018 Question Papers |
Also Check:





Comments