GATE 2022 Instrumentation Engineering (IN) Question Paper with Solutions can be downloaded for free. GATE 2022 IN was successfully concluded on 6th February 2022 in the Afternoon Session (2:30 PM to 5:30 PM). This year IIT Kharagpur took the charge to conduct GATE 2022 IN. As per the candidates, the question paper of GATE 2022 IN was moderately difficult. The overall question paper was divided into three sections i.e General Aptitude, Engineering Mathematics, and Topics related to core Instrumentation Engineering.
GATE 2022 Instrumentation Engineering (IN) Question Paper with Solutions
| GATE 2022 Instrumentation Engineering (IN) Question Paper | Check Solutions |

Inhaling the smoke from a burning __________ could __________ you quickly.
A sphere of radius \(r\) cm is packed in a box of cubical shape.
What should be the minimum volume (in cm\(^3\)) of the box that can enclose the sphere?
Pipes P and Q can fill a storage tank in full with water in 10 and 6 minutes, respectively. Pipe R draws the water out from the storage tank at a rate of 34 litres per minute. P, Q and R operate at a constant rate.
If it takes one hour to completely empty a full storage tank with all the pipes operating simultaneously, what is the capacity of the storage tank (in litres)?
Six persons P, Q, R, S, T, and U are sitting around a circular table facing the center not necessarily in the same order. Consider the following statements:
P sits next to S and T.
Q sits diametrically opposite to P.
The shortest distance between S and R is equal to the shortest distance between T and U.
Based on the above statements, Q is a neighbor of
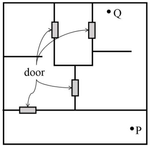
A building has several rooms and doors as shown in the top view of the building given below. The doors are closed initially.
What is the minimum number of doors that need to be opened in order to go from the point P to the point Q?
Rice, a versatile and inexpensive source of carbohydrate, is a critical component of diet worldwide. Climate change, causing extreme weather, poses a threat to sustained availability of rice. Scientists are working on developing Green Super Rice (GSR), which is resilient under extreme weather conditions yet gives higher yields sustainably.
Which one of the following is the CORRECT logical inference based on the information given in the above passage?
A game consists of spinning an arrow around a stationary disk as shown below.
When the arrow comes to rest, there are eight equally likely outcomes. It could come to rest in any one of the sectors numbered 1, 2, 3, 4, 5, 6, 7, or 8 as shown.
Two such disks are used in a game where their arrows are independently spun.
What is the probability that the sum of the numbers on the resulting sectors upon spinning the two disks is equal to 8 after the arrows come to rest?

Consider the following inequalities.
(i) \( 3p - q < 4 \)
(ii) \( 3q - p < 12 \)
Which one of the following expressions below satisfies the above two inequalities?
Given below are three statements and four conclusions drawn based on the statements.
Statement 1: Some engineers are writers.
Statement 2: No writer is an actor.
Statement 3: All actors are engineers.
Conclusion I: Some writers are engineers.
Conclusion II: All engineers are actors.
Conclusion III: No actor is a writer.
Conclusion IV: Some actors are writers.
Which one of the following options can be logically inferred?
Which one of the following sets of pieces can be assembled to form a square with a single round hole near the center? Pieces cannot overlap.

The input \( x(t) \) to a system is related to its output \( y(t) \) as
\[ \frac{d y(t)}{dt} + y(t) = 3x(t - 3)u(t - 3) \]
\text{Here \( u(t) \) represents a unit-step function.
\text{The transfer function of this system is _________
A pneumatic nozzle-flapper system is conventionally used to convert _________
A periodic function \( f(x) \), with period 2, is defined as \[ f(x) = \begin{cases} -1 - x & for -1 \leq x < 0
1 - x & for 0 \leq x \leq 1 \end{cases} \]
The Fourier series of this function contains _________
The output of a system \( y(t) \) is related to its input \( x(t) \) according to the relation \( y(t) = x(t) \sin(2\pi t) \). This system is _________
A unity-gain negative-feedback control system has a loop-gain \( L(s) \) given by \[ L(s) = \frac{6}{s(s-5)} \]
The closed-loop system is _________
A sinusoidal carrier wave with amplitude \( A_c \) and frequency \( f_c \) is amplitude modulated with a message signal \( m(t) \) having frequency \( 0 < f_m \ll f_c \) to generate the modulated wave \( s(t) \) given by \[ s(t) = A_c[1 + m(t)]\cos(2\pi f_c t) \]
The message signal that can be retrieved completely using envelope detection is _________
A Hall sensor is based on the principle of _________
A signal \( x(t) \) is band-limited between 100 Hz and 200 Hz. A signal \( y(t) \) is related to \( x(t) \) as follows:
y(t) = x(2t - 5)
The statement that is always true is_________
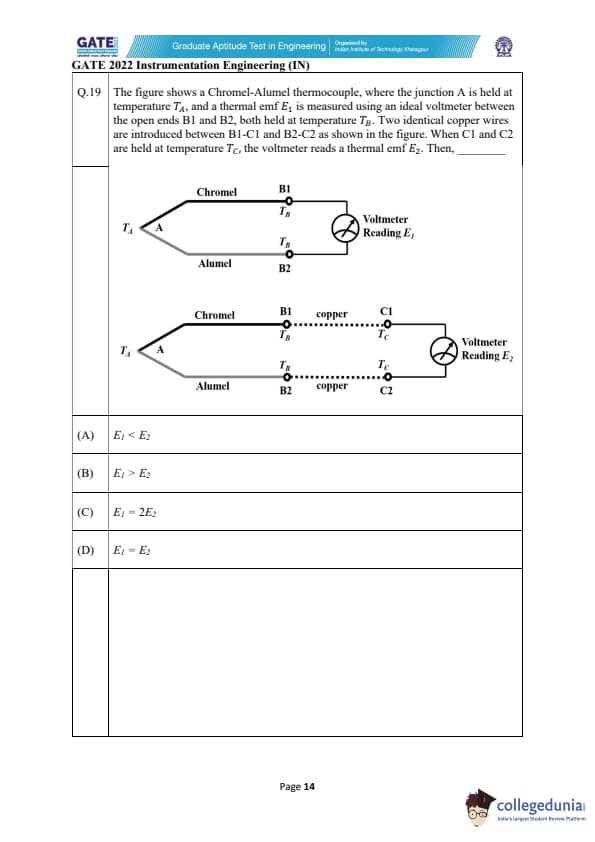
The figure shows a Chromel-Alumel thermocouple, where the junction A is held at temperature \( T_A \), and a thermal emf \( E_1 \) is measured using an ideal voltmeter between the open ends B1 and B2, both held at temperature \( T_B \). Two identical copper wires are introduced between B1-C1 and B2-C2 as shown in the figure. When C1 and C2 are held at temperature \( T_C \), the voltmeter reads a thermal emf \( E_2 \). Then, _________

The resistance of a pure copper wire of length 10 cm and diameter 1 mm is to be measured. The most suitable method from amongst the choices given below is _________.
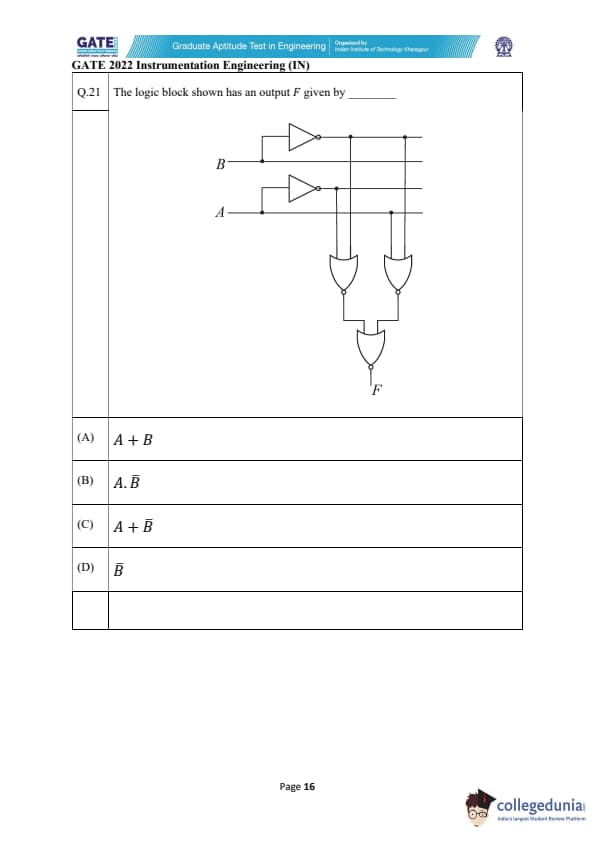
The logic block shown has an output \( F \) given by _________

In which of the following bridge(s) is the balancing condition frequency-independent?
The output F of the digital circuit shown can be written in the form _________

Given \( M = \begin{bmatrix} 2 & 3 & 7
6 & 4 & 7
4 & 6 & 14 \end{bmatrix} \), which of the following statement(s) is/are correct?
An analog-to-digital converter with resolution 0.01 V converts analog signals between 0 V to +10 V to an unsigned binary output. The minimum number of bits (in integer) in the output is _________
Consider 24 voice signals being transmitted without latency using time-division multiplexing. If each signal is sampled at 12 kHz and represented by an 8-bit word, the bit-duration (in microseconds) is _________ (round off to two decimal places)
A photodiode is made of a semiconductor with a bandgap of 1.42 eV. Given that Planck’s constant is \(6.626 \times 10^{-34}\) J·s, the speed of light in vacuum is \(3 \times 10^8\) m/s, and \(1 \, eV = 1.6 \times 10^{-19}\) J, the cut-off wavelength (in nanometers) of the photodiode is _________ (round off to one decimal place).
The global minimum of \(x^3 e^{-|x|}\) for \(x \in (-\infty, \infty)\) occurs at \(x =\) _________ (round off to one decimal place).
A 440 V, 8 kW, 4-pole, 50 Hz, star-connected induction motor has a full load slip of 0.04. The rotor speed (in rpm) at full load is _________.
The transfer function of a system is: \[ \frac{(s + 1)(s + 3)}{(s + 5)(s + 7)(s + 9)}. \]
In the state-space representation of the system, the minimum number of state variables (in integer) necessary is _________.
A Zener diode is used as a 4 V voltage regulator in the circuit shown. Given that the diode requires a minimum current of 4 mA for voltage regulation, the maximum current (in milliamperes) permitted to flow through the load \( R_L \) is _________ (round off to one decimal place)

A bag contains six red balls and four blue balls. If three balls are drawn in succession without replacement, the probability that the second and third balls drawn are red is _________ (round off to two decimal places)
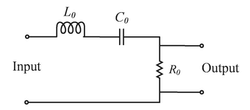
In the bandpass filter circuit shown, \( R_0 = 50 \, \Omega \), \( L_0 = 1 \, mH \), \( C_0 = 10 \, nF \). The Q factor of the filter is _________ (round off to two decimal places).
The Newton-Raphson method is applied to determine the solution of \( f(x) = 0 \) where \( f(x) = x - \cos(x) \). If the initial guess of the solution is \( x_0 = 0 \), the value of the next approximation \( x_1 \) is _________ (round off to two decimal places).
An OPAMP has a gain of \( 10^4 \), an input impedance of 10 MΩ and an output impedance of 100Ω. The OPAMP is used in unity-gain feedback configuration in a voltage buffer circuit. The closed-loop output impedance of the OPAMP (in milliohms) in the circuit is _________.
A signal \( V_{in}(t) \) shown is applied from \( t = 0 \) ms to \( t = 6 \) ms to the circuit shown. Given the initial voltage across the capacitor is 0.3 V, and that the diode is ideal, the open circuit voltage \( V_{out}(t) \) at \( t = 5 \) ms is _________

The signal flow graph of a system is shown. The expression for \( Y(s)/X(s) \) is _________ .

Consider the transfer function \[ H_c(s) = \frac{1}{(s + 1)(s + 3)} \]
Bilinear transformation with a sampling period of 0.1 s is employed to obtain the discrete-time transfer function \( H_d(z) \). Then \( H_d(z) \) is _________
A car is moving collinearly with a laser beam emitted by a transceiver. A laser pulse emitted at \( t = 0 \) s is received back by the transceiver 100 ns (nanoseconds) later after reflection from the car. A second pulse emitted at \( t = 0.1 \) s is received back 90 ns later. Given the speed of light is \( 3 \times 10^8 \) m/s, the average speed of the car in this interval is _________
The signal \( x(t) = (t - 1)^2 u(t - 1) \), where \( u(t) \) is the unit-step function, has the Laplace transform \( X(s) \). The value of \( X(1) \) is_________
A proportional-integral-derivative (PID) controller is employed to stably control a plant with transfer function \[ P(s) = \frac{1}{(s + 1)(s + 2)}. \]
Now, the proportional gain is increased by a factor of 2, the integral gain is increased by a factor of 3, and the derivative gain is left unchanged. Given that the closed-loop system continues to remain stable with the new gains, the steady-state error in tracking a ramp reference signal_________
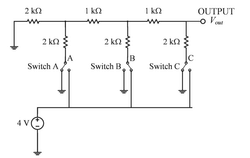
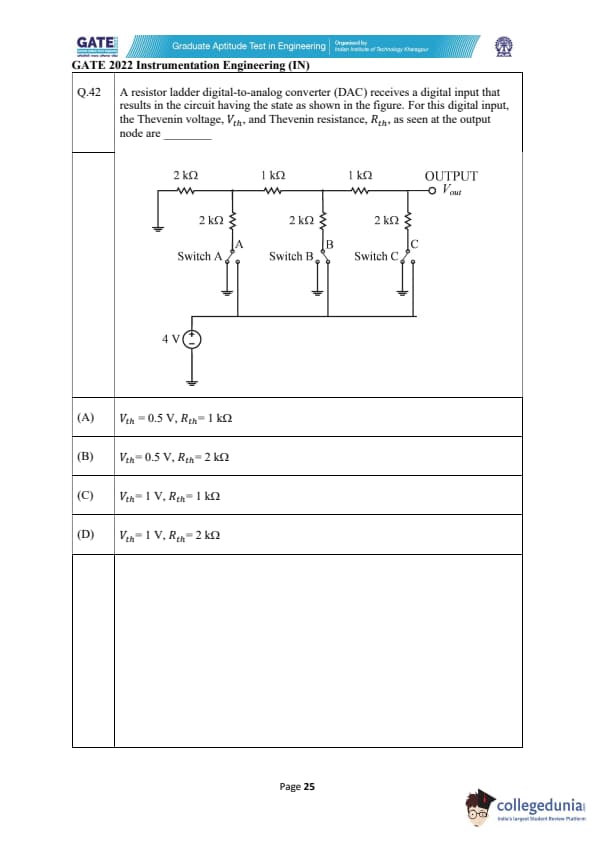
A resistor ladder digital-to-analog converter (DAC) receives a digital input that results in the circuit having the state as shown in the figure. For this digital input, the Thevenin voltage, \( V_{th} \), and Thevenin resistance, \( R_{th} \), as seen at the output node are _________
The Nyquist plot of a stable open-loop system \( G(j\omega) \) is plotted in the frequency range \( 0 \leq \omega < \infty \) as shown. It is found to intersect a unit circle with center at the origin at the point \( P = -0.77 - 0.64j \). The points \( Q \) and \( R \) lie on \( G(j\omega) \) and assume values \( Q = 14.40 + 0.00j \) and \( R = -0.21 + 0.00j \). The phase margin (PM) and the gain margin (GM) of the system are _________

In the small signal circuit shown, the enhancement mode n-channel MOSFET is biased in saturation with transconductance \( g_m \). If channel length modulation is ignored, the small signal impedance looking into the node P is given by _________

Consider the differential equation \[ \frac{dy}{dx} + y \ln(y) = 0 \]
If \( y(0) = e \), then \( y(1) \) is _________ .
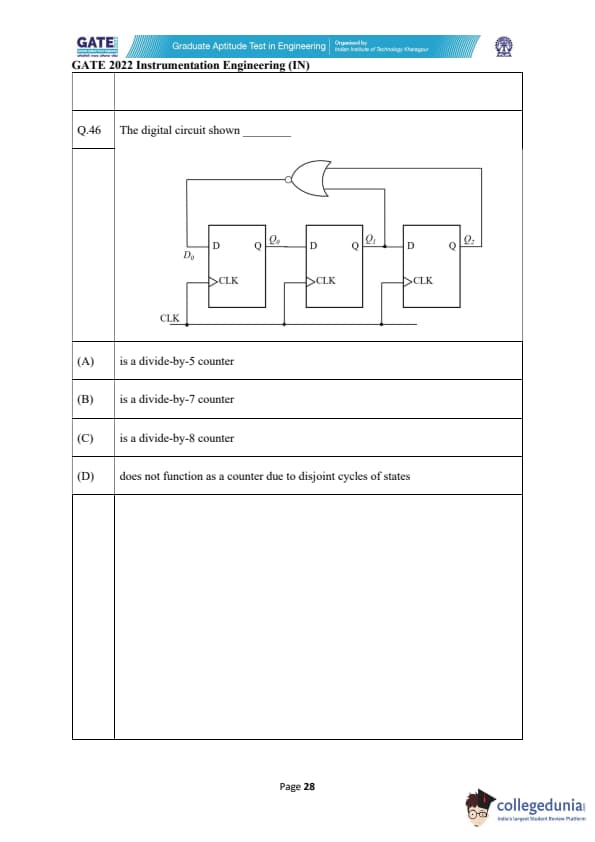
The digital circuit shown _________ .

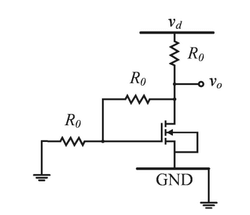
In the small signal circuit shown, the enhancement mode n-channel MOSFET is biased in saturation with a transconductance \( g_m \). A small signal low-frequency voltage \( v_d \) injected at the supply terminal results in a small signal voltage fluctuation \( v_o \) at the output. If the channel length modulation of the MOSFET is ignored, the small signal gain \( \frac{v_o}{v_d} \) is given by _________
A = \( a_1a_0 \) and B = \( b_1b_0 \) are two 2-bit unsigned binary numbers. If \( F(a_1, a_0, b_1, b_0) \) is a Boolean function such that \( F = 1 \) only when \( A > B \), and \( F = 0 \) otherwise, then \( F \) can be minimized to the form _________
The matrix \[ A = \begin{bmatrix} 4 & 3
9 & -2 \end{bmatrix} \]
has eigenvalues -5 and 7. The eigenvector(s) is/are _________
For the complex number \( Z = \frac{a + jb}{a - jb} \), where \( a > 0 \) and \( b > 0 \). Which of the following statement(s) is/are true?
Monochromatic light of wavelength 532 nm is used to measure the absorption coefficient of a material in a UV-Visible Spectrophotometer. The measured light intensity after transmission through a 1 cm thick sample of the material is 0.414 mW/cm\(^2\). For a sample of thickness 2 cm, the measured light intensity is 0.186 mW/cm\(^2\). The absorption coefficient (in cm\(^{-1}\)) of the material is _________ (round off to two decimal places)
In the circuit shown, the load is driven by a sinusoidal ac voltage source \( V_1 = 100 \angle 0^\circ \, V \) at 50 Hz. Given \( R_1 = 20 \, \Omega \), \( C_1 = \left(\frac{1000}{\pi}\right) \, \muF \), \( L_1 = \left(\frac{20}{\pi}\right) \, mH \), and \( R_2 = 4 \, \Omega \), the power factor is _________ (round off to one decimal place)

In a unity-gain feedback control system, the plant \[ P(s) = \frac{0.001}{s(2s + 1)(0.01s + 1)} \]
is controlled by a lag compensator \[ C(s) = \frac{s + 10}{s + 0.1} \]
The slope (in dB/decade) of the asymptotic Bode magnitude plot of the loop gain at \( \omega = 3 \, rad/s \) is _________ (in integer).
Given Circuit A with currents \(I_1\) and \(I_2\) as shown, the current \(I_3\) in Circuit B (in amperes) is _________ (round off to one decimal place).

In the balanced three-phase circuit shown, \( C_0 = 8.2 \, \mu F \) and the line-to-line r.m.s. voltage is 440 V at 50 Hz. The reading on the wattmeter (in watts) is _________.

The circuit shown is driven by a sinusoidal input voltage, \( V_{in} \), resulting in the output voltage, \( V_{out} \). The frequency (in kilohertz) at which the voltage gain is 0 dB is _________ (round off to two decimal places)

A conducting semi-circular loop of radius \( R = 0.1 \, m \), with its diameter centered at the origin, rotates in the \( x \)-\( y \) plane about the origin with a constant angular velocity, \( \omega = 20 \, rad/s \), as shown. A magnetic field of magnitude \( B = 2 \, T \) and normal to the \( x \)-\( y \) plane exists in the region \( x \geq 0 \) as shown. If the loop has a resistance of \( 2 \, \Omega \), and negligible inductance, the peak-to-peak current (in milliamperes) in the loop is _________ (round off to one decimal place)

In the circuit shown, \(R_1 = 100 \, k\Omega\) and \(R_2 = 1 \, k\Omega\). If the base-to-emitter voltage of the npn BJT is 0.7 V and the collector-to-emitter voltage is 5.2 V, the \(\beta\) (current gain) of the BJT is _________ (round off to two decimal places).
A capacitor is constructed using two concentric spheres and air as the dielectric medium (permittivity of air = \(8.854 \times 10^{-12} \, F/m\)). The radii of the inner and outer spheres are \(a = 10 \, cm\) and \(b = 15 \, cm\), respectively. The capacitance (in picofarads) is _________ (round off to 2 decimal places).
A 1 kHz sine-wave generator having an internal resistance of 50Ω generates an open-circuit voltage of 10 Vp-p. When a capacitor is connected across the output terminals, the voltage drops to 8 Vp-p. The capacitance of the capacitor (in microfarads) is _________.
Consider the function \( f(z) = \frac{1}{(z+1)(z+2)(z+3)} \). The residue of \( f(z) \) at \( z = -1 \) is _________.
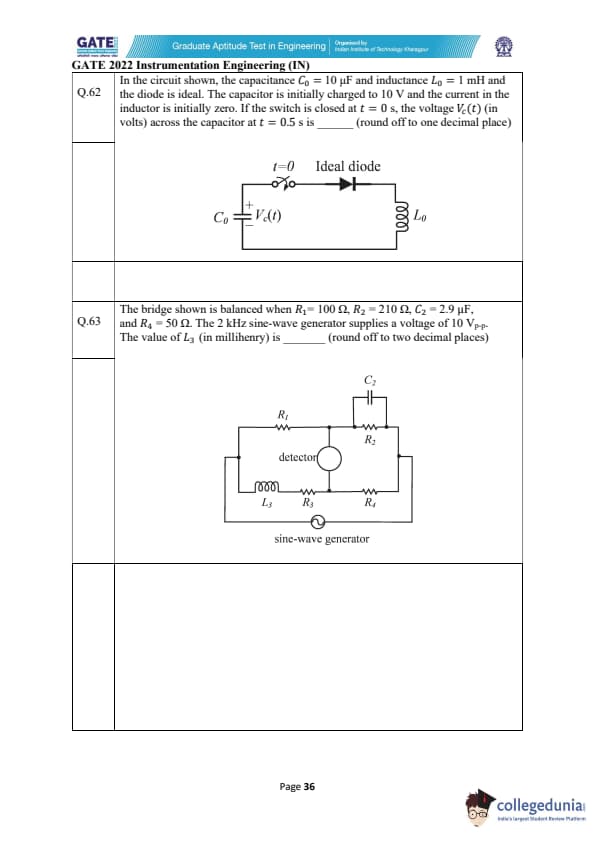
In the circuit shown, the capacitance \( C_0 = 10 \, \muF \) and inductance \( L_0 = 1 \, mH \) and the diode is ideal. The capacitor is initially charged to 10 V and the current in the inductor is initially zero. If the switch is closed at \( t = 0 \, s \), the voltage \( V_C(t) \) (in volts) across the capacitor at \( t = 0.5 \, s \) is _________ (round off to one decimal place)

The bridge shown is balanced when \( R_1 = 100 \, \Omega \), \( R_2 = 210 \, \Omega \), \( C_2 = 2.9 \, \muF \), and \( R_4 = 50 \, \Omega \). The 2 kHz sine-wave generator supplies a voltage of 10 V\(_p-p\). The value of \( L_3 \) (in millihenry) is _________ (round off to two decimal places)

In the circuit shown, the switch is initially closed. It is opened at \( t = 0 \, s \) and remains open thereafter. The time (in milliseconds) at which the output voltage \( V_{out} \) becomes LOW is _________ (round off to three decimal places).
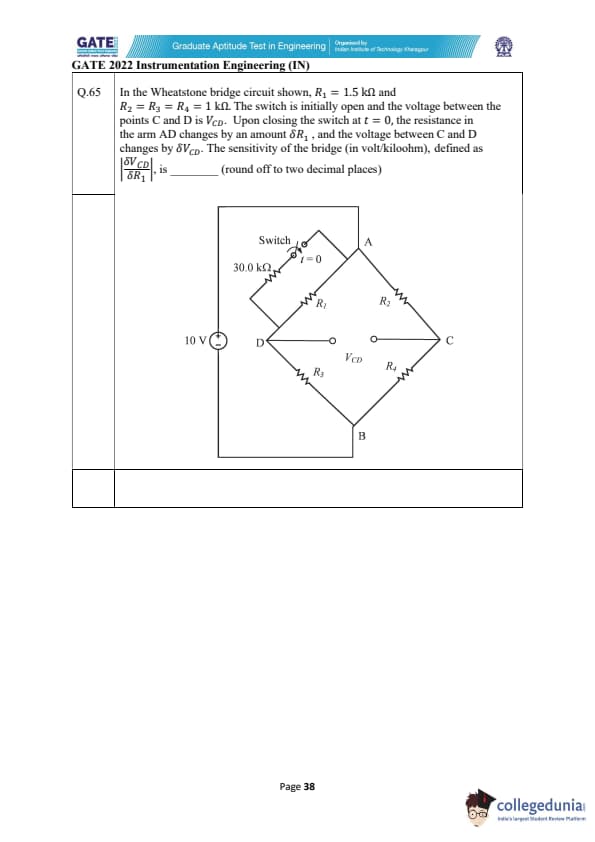
In the Wheatstone bridge circuit shown, \( R_1 = 1.5 \, k\Omega \) and \( R_2 = R_3 = R_4 = 1 \, k\Omega \). The switch is initially open and the voltage between the points C and D is \( V_{CD} \). Upon closing the switch at \( t = 0 \), the resistance in the arm AD changes by an amount \( \delta R_1 \), and the voltage between C and D changes by \( \delta V_{CD} \). The sensitivity of the bridge in volt/kilohm, defined as \( \left| \frac{\delta V_{CD}}{\delta R_1} \right| \), is _________.


































Quick Links:
GATE 2022 IN Detailed Paper Analysis
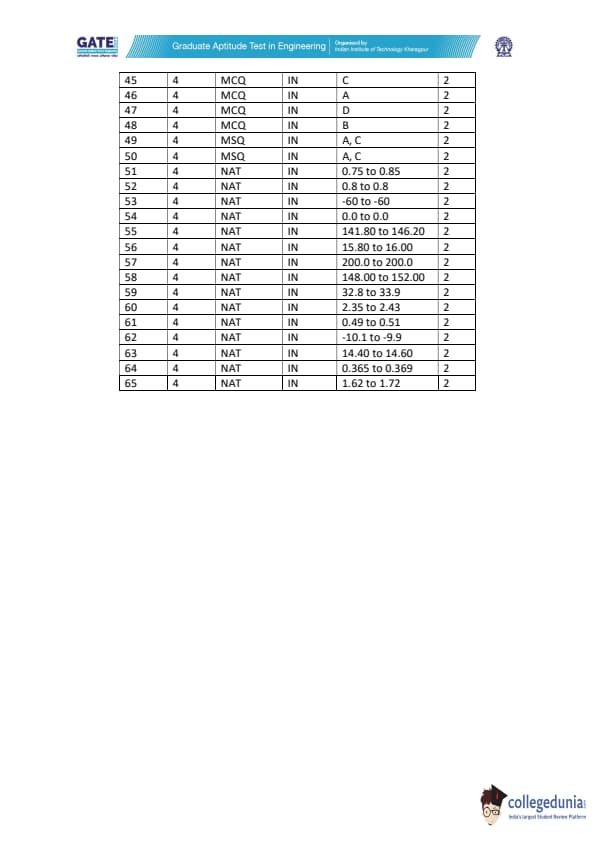
A total of 65 questions appeared in the GATE 2022 IN question paper. IIT Kharagpur categorised the questions in three categories i.e. MCQs (Multiple Choice Questions), MSQs (Multiple Select Questions), and NATs (Numerical Answer Type) questions. The below-mentioned table showing the details of the questions as per the carried marks-
| Question Types | Question Frequency | Carried Marks |
|---|---|---|
| No. Of 1 Mark MSQs | 3 | 3 |
| No. Of 2 Marks MSQs | 2 | 4 |
| No. Of 1 Mark MCQs | 16 | 16 |
| No. Of 2 Marks MCQs | 18 | 36 |
| No. Of 1 Mark NATs | 11 | 11 |
| No. Of 2 Marks NATs | 15 | 30 |
| Total | 65 | 100 |
- There were only 5 MSQs made a spot in GATE 2022 IN question paper, carrying 7% of the total weightage
- MCQs were responsible for carrying 52%, while NATs carried 41% of the total weightage
- The General Aptitude section carried a total of 15 marks. It carries 5 questions carrying 2 marks and 5 questions carrying 1 mark
- The General Aptitude section was the easiest section to attempt
- Cutoff for GATE 2022 IN goes upto 42.4 for General/Unreserved students, 38.1 and 28.2 for OBC NCL and SC/ST/PwD candidates respectively
Also Check:
GATE Previous Year Question Papers:
| GATE 2022 Question Papers | GATE 2021 Question Papers | GATE 2020 Question Papers |
| GATE 2019 Question Papers | GATE 2018 Question Papers | GATE 2017 Question Papers |





Comments