GATE 2022 Civil Engineering (CE) Slot-1 Question Paper with Solutions pdfs is available. GATE 2022 CE Slot 1 was conducted on 12th February from 9:00 AM to 12:00 PM by IIT Kharagpur. The test-takers rated the overall difficulty to be moderate to tough. The General Aptitude section carried the highest weightage in GATE 2022 CE Slot 1 question paper. Chapters such as Environmental Soil and Geotechnical Engineering carried the highest weightage among core Civil Engineering topics. No question in GATE 2022 CE question paper for slot 1 was rated easy by the test takers.
Students planning to appear in GATE 2023 can download and solve GATE 2022 CE Question Paper with Answer Key PDFs Slot 1 from the links given below.
GATE 2022 Civil Engineering (CE) Slot-1 Question Paper with Solutions
| GATE 2022 Civil Engineering (CE) Slot-1 Question Paper | Check Solutions |

You should ______ when to say ______.
Two straight lines pass through the origin \( (x_0, y_0) = (0, 0) \). One of them passes through the point \( (x_1, y_1) = (1, 3) \) and the other passes through the point \( (x_2, y_2) = (1, 2) \). What is the area enclosed between the straight lines in the interval \( [0, 1] \) on the x-axis?
If \[ p : q = 1 : 2, \quad q : r = 4 : 3, \quad r : s = 4 : 5 \]
and \( u \) is 50% more than \( s \), what is the ratio \( p : u \)?
Given the statements:
P is the sister of Q.
Q is the husband of R.
R is the mother of S.
T is the husband of P.
Based on the above information, T is _________ of S.
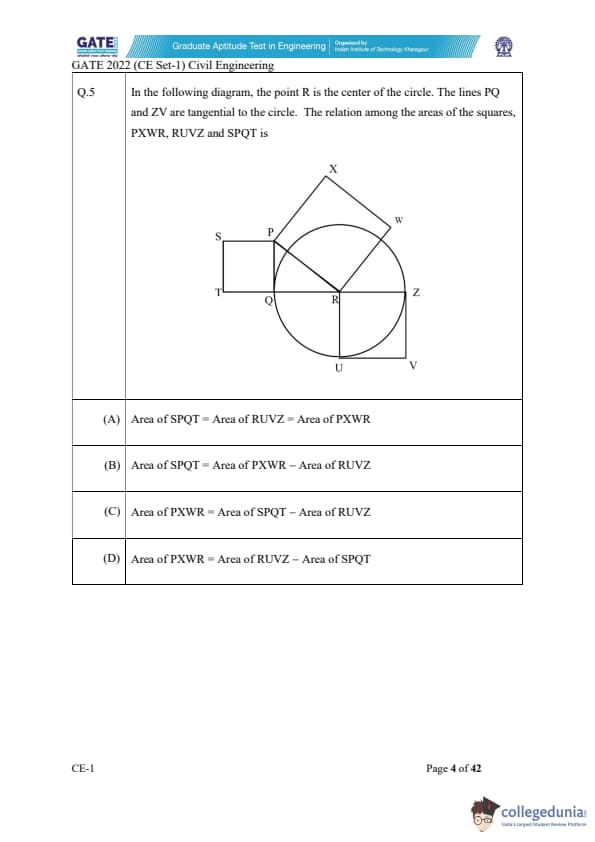
In the following diagram, the point R is the center of the circle. The lines PQ and ZV are tangential to the circle. The relation among the areas of the squares, PXWR, RUVZ and SPQT is

Healthy eating is a critical component of healthy aging. When should one start eating healthy? It turns out that it is never too early. For example, babies who start eating healthy in the first year are more likely to have better overall health as they get older.
P invested ₹ 5000 per month for 6 months of a year and Q invested ₹ x per month for 8 months of the year in a partnership business. The profit is shared in proportion to the total investment made in that year.
If at the end of that investment year, Q receives \( \frac{4}{9} \) of the total profit, what is the value of \( x \) (in ₹)?
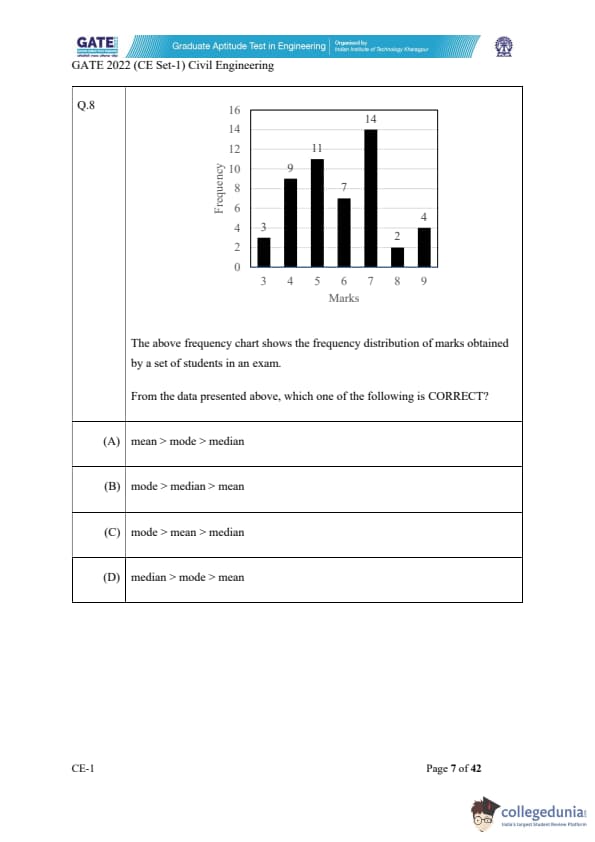
The above frequency chart shows the frequency distribution of marks obtained by a set of students in an exam.
From the data presented above, which one of the following is CORRECT?

In the square grid shown on the left, a person standing at P2 position is required to move to P5 position.
The only movement allowed for a step involves, "two moves along one direction followed by one move in a perpendicular direction". The permissible directions for movement are shown as dotted arrows in the right.
For example, a person at a given position Y can move only to the positions marked X on the right.
Without occupying any of the shaded squares at the end of each step, the minimum number of steps required to go from P2 to P5 is:

Consider a cube made by folding a single sheet of paper of appropriate shape. The interior faces of the cube are all blank. However, the exterior faces that are not visible in the above view may not be blank. Which one of the following represents a possible unfolding of the cube?


Consider the following expression: \[ z = \sin(y + it) + \cos(y - it) \]
where \( z \), \( y \), and \( t \) are variables, and \( i = \sqrt{-1} \) is a complex number. The partial differential equation derived from the above expression is
For the equation \[ \frac{d^3 y}{dx^3} + x \left( \frac{dy}{dx} \right)^{3/2} + x^2 y = 0 \]
the correct description is
The hoop stress at a point on the surface of a thin cylindrical pressure vessel is computed to be 30.0 MPa. The value of maximum shear stress at this point is
In the context of elastic theory of reinforced concrete, the modular ratio is defined as the ratio of
Which of the following equations is correct for the Pozzolanic reaction?
Consider the cross-section of a beam made up of thin uniform elements having thickness \( t \) (where \( t \ll a \)) shown in the figure. The (x, y) coordinates of the points along the center-line of the cross-section are given in the figure.
The coordinates of the shear center of this cross-section are:

Four different soils are classified as CH, ML, SP, and SW, as per the Unified Soil Classification System. Which one of the following options correctly represents their arrangement in the decreasing order of hydraulic conductivity?
Let \( \sigma_{\nu}' \) and \( \sigma_{h}' \) denote the effective vertical stress and effective horizontal stress, respectively. Which one of the following conditions must be satisfied for a soil element to reach the failure state under Rankine’s passive earth pressure condition?
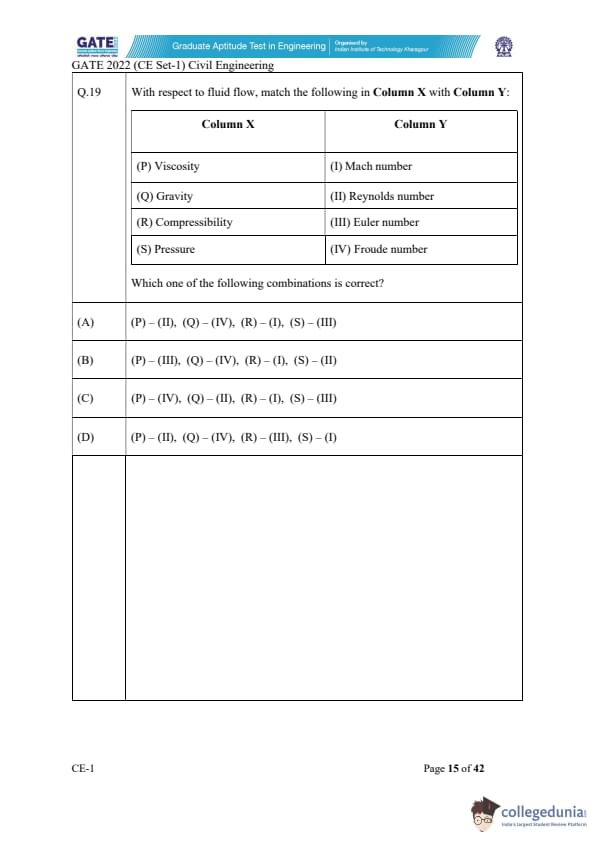
With respect to fluid flow, match the following in Column X with Column Y:
Which one of the following combinations is correct?

Let \( \psi \) represent soil suction head and \( K \) represent hydraulic conductivity of the soil. If the soil moisture content \( \theta \) increases, which one of the following statements is TRUE?
A rectangular channel with Gradually Varied Flow (GVF) has a changing bed slope. If the change is from a steeper slope to a steep slope, the resulting GVF profile is
The total hardness in raw water is 500 milligram per liter as CaCO\(_3\). The total hardness of this raw water, expressed in milligram equivalent per liter, is
An aerial photograph is taken from a flight at a height of 3.5 km above mean sea level, using a camera of focal length 152 mm. If the average ground elevation is 460 m above mean sea level, then the scale of the photograph is
A line between stations P and Q laid on a slope of 1 in 5 was measured as 350 m using a 50 m tape. The tape is known to be short by 0.1 m.
The corrected horizontal length (in m) of the line PQ will be:
The matrix \( M \) is defined as \[ M = \begin{bmatrix} 1 & 3
4 & 2 \end{bmatrix} \]
and has eigenvalues 5 and -2. The matrix \( Q \) is formed as \[ Q = M^3 - 4M^2 - 2M \]
Which of the following is/are the eigenvalue(s) of matrix \( Q \)?
For wastewater coming from a wood pulping industry, Chemical Oxygen Demand (COD) and 5-day Biochemical Oxygen Demand (BOD\(_5\)) were determined. For this wastewater, which of the following statement(s) is/are correct?
Which of the following process(es) can be used for conversion of salt water into fresh water?
A horizontal curve is to be designed in a region with limited space. Which of the following measure(s) can be used to decrease the radius of curvature?
Consider the following recursive iteration scheme for different values of variable P with the initial guess \( x_1 = 1 \):
\[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{P}{x_n} \right), \quad n = 1, 2, 3, 4, 5 \]
For \( P = 2 \), \( x_5 \) is obtained to be 1.414, rounded-off to three decimal places. For \( P = 3 \), \( x_5 \) is obtained to be 1.732, rounded-off to three decimal places.
If \( P = 10 \), the numerical value of \( x_5 \) is ________ (round off to three decimal places).
The Fourier cosine series of a function is given by:
\[ f(x) = \sum_{n=0}^{\infty} f_n \cos nx \]
For \( f(x) = \cos^4 x \), the numerical value of \( (f_4 + f_5) \) is ________ (round off to three decimal places).
An uncompacted heap of soil has a volume of 10000 m\(^3\) and void ratio of 1. If the soil is compacted to a volume of 7500 m\(^3\), then the corresponding void ratio of the compacted soil is ________ (round off to one decimal place).
A concentrated vertical load of 3000 kN is applied on a horizontal ground surface. Points P and Q are at depths 1 m and 2 m below the ground, respectively, along the line of application of the load. Considering the ground to be a linearly elastic, isotropic, semi-infinite medium, the ratio of the increase in vertical stress at P to the increase in vertical stress at Q is ________ (in integer).
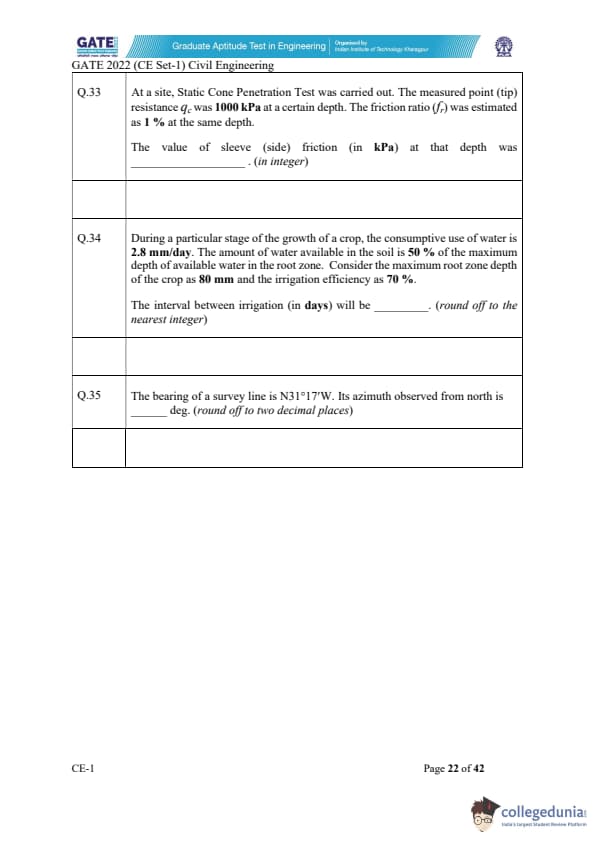
At a site, Static Cone Penetration Test was carried out. The measured point (tip) resistance \( q_c \) was 1000 kPa at a certain depth. The friction ratio (\( f_r \)) was estimated as 1 % at the same depth.
The value of sleeve (side) friction (in kPa) at that depth was ________ . (in integer)
During a particular stage of the growth of a crop, the consumptive use of water is 2.8 mm/day. The amount of water available in the soil is 50 % of the maximum depth of available water in the root zone. Consider the maximum root zone depth of the crop as 80 mm and the irrigation efficiency as 70 %.
The interval between irrigation (in days) will be ________ . (round off to the nearest integer)
The bearing of a survey line is N31°17′W. Its azimuth observed from north is ________ degrees. (round off to two decimal places)
The Cartesian coordinates of a point P in a right-handed coordinate system are (1, 1, 1). The transformed coordinates of P due to a 45° clockwise rotation of the coordinate system about the positive x-axis are
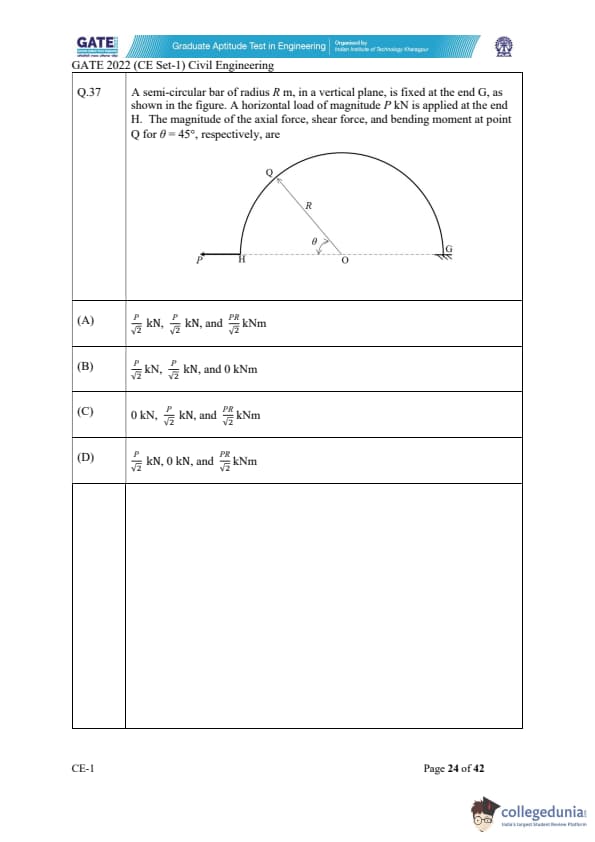
A semi-circular bar of radius R m, in a vertical plane, is fixed at the end G, as shown in the figure. A horizontal load of magnitude P kN is applied at the end H. The magnitude of the axial force, shear force, and bending moment at point Q for \(\theta = 45^\circ\), respectively, are

A weld is used for joining an angle section ISA 100 mm \(\times\) 100 mm \(\times\) 10 mm to a gusset plate of thickness 15 mm to transmit a tensile load. The permissible stress in the angle is 150 MPa and the permissible shear stress on the section through the throat of the fillet weld is 108 MPa. The location of the centroid of the angle is represented by \( C_{yy} \) in the figure, where \( C_{yy} = 28.4 \, mm \). The area of cross-section of the angle is 1903 mm\(^2\). Assuming the effective throat thickness of the weld to be 0.7 times the given weld size, the lengths \( L_1 \) and \( L_2 \) (rounded off to the nearest integer) of the weld required to transmit a load equal to the full strength of the tension member are, respectively

The project activities are given in the following table along with the duration and dependency.

Which one of the following combinations is correct?
The correct match between the physical states of the soils given in Group I and the governing conditions given in Group II is

As per Rankine’s theory of earth pressure, the inclination of failure planes is \[ \left( 45^\circ + \frac{\phi}{2} \right) \]
with respect to the direction of the minor principal stress. The above statement is correct for which one of the following options?
Henry’s law constant for transferring \( O_2 \) from air into water, at room temperature, is 1.3 \[ \frac{mmol}{liter-atm} \]
. Given that the partial pressure of \( O_2 \) in the atmosphere is 0.21 atm, the concentration of dissolved oxygen (mg/liter) in water in equilibrium with the atmosphere at room temperature is \[ (Consider the molecular weight of O_2 as 32 g/mol) \]
In a water sample, the concentrations of Ca\(^{2+}\), Mg\(^{2+}\) and HCO\(_3^-\) are 100 mg/L, 36 mg/L and 122 mg/L, respectively. The atomic masses of various elements are: Ca = 40, Mg = 24, H = 1, C = 12, O = 16.
The total hardness and the temporary hardness in the water sample (in mg/L as CaCO\(_3\)) will
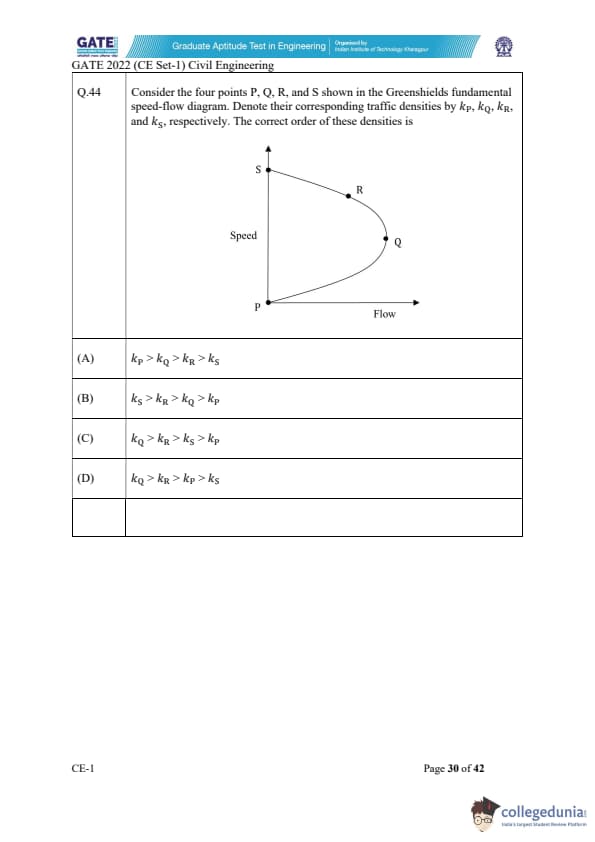
Consider the four points P, Q, R, and S shown in the Greenshields fundamental speed-flow diagram. Denote their corresponding traffic densities by \( k_P \), \( k_Q \), \( k_R \), and \( k_S \), respectively. The correct order of these densities is:

Let max {a, b} denote the maximum of two real numbers a and b.
Which of the following statement(s) is/are TRUE about the function \[ f(x) = max\{3 - x, x - 1\}? \]
A horizontal force of P kN is applied to a homogeneous body of weight 25 kN, as shown in the figure. The coefficient of friction between the body and the floor is 0.3. Which of the following statement(s) is/are correct?

In the context of cross-drainage structures, the correct statement(s) regarding the relative positions of a natural drain (stream/river) and an irrigation canal, is/are
Consider the differential equation \[ \frac{dy}{dx} = 4(x + 2) - y \]
For the initial condition \( y = 3 \) at \( x = 1 \), the value of \( y \) at \( x = 1.4 \) obtained using Euler’s method with a step-size of 0.2 is ________ . (round off to one decimal place)
A set of observations of independent variable \( x \) and the corresponding dependent variable \( y \) is given below.

Based on the data, the coefficient \( a \) of the linear regression model \[ y = a + bx \]
is estimated as 6.1. The coefficient \( b \) is ________ . (round off to one decimal place)
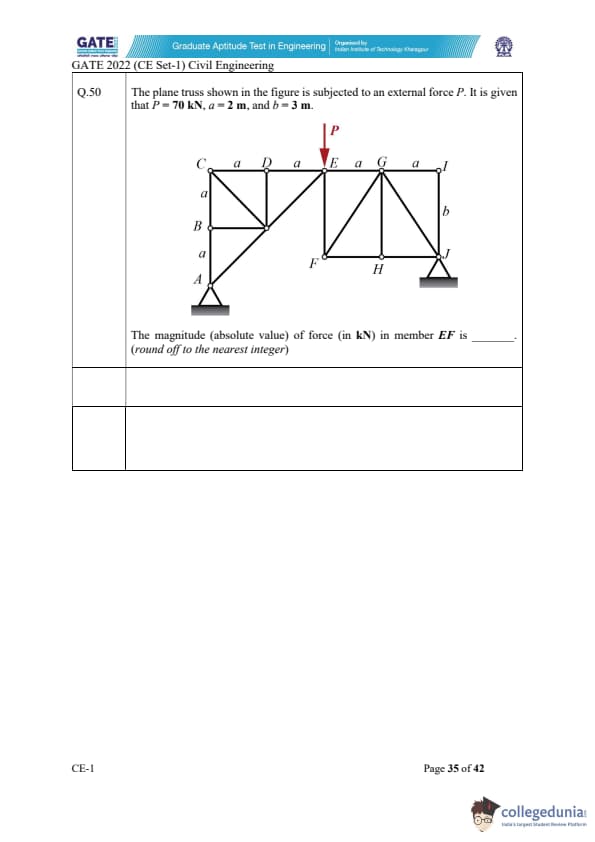
The plane truss shown in the figure is subjected to an external force \( P \). It is given that \( P = 70 \, kN \), \( a = 2 \, m \), and \( b = 3 \, m \).

The magnitude (absolute value) of force in member EF is ______ (round off to the nearest integer).
Consider the linearly elastic plane frame shown in the figure. Members HF, FK, and FG are welded together at joint F. Joints K, G, and H are fixed supports. A counter-clockwise moment \( M \) is applied at joint F. Consider flexural rigidity \( EI = 10^5 \, kN-m^2 \) for each member and neglect axial deformations.

If the magnitude (absolute value) of the support moment at H is 10 kN-m, the magnitude (absolute value) of the applied moment \( M \) (in kN-m) to maintain static equilibrium is ______ (round off to the nearest integer).
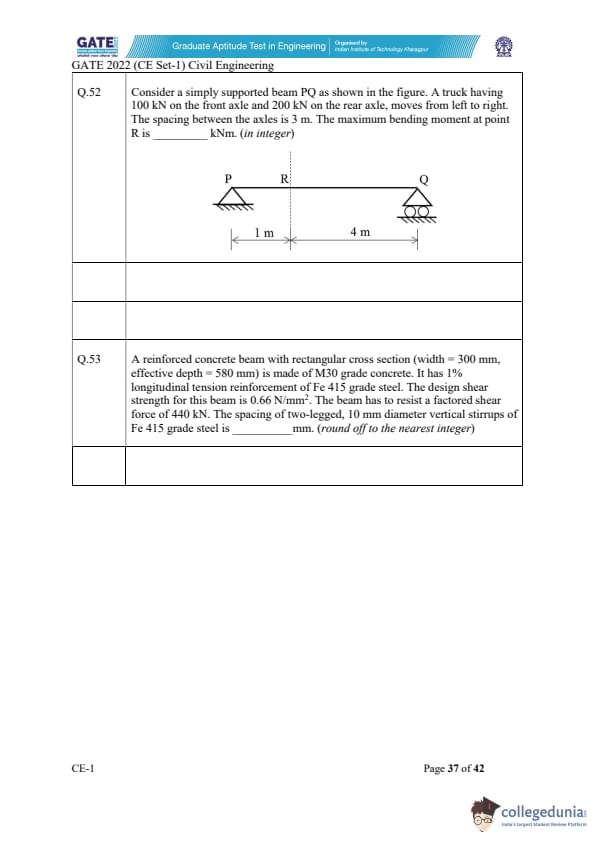
Consider a simply supported beam PQ as shown in the figure. A truck having 100 kN on the front axle and 200 kN on the rear axle, moves from left to right. The spacing between the axles is 3 m. The maximum bending moment at point R is ________ kNm. (in integer)

A reinforced concrete beam with rectangular cross section (width = 300 mm, effective depth = 580 mm) is made of M30 grade concrete. It has 1% longitudinal tension reinforcement of Fe 415 grade steel. The design shear strength for this beam is 0.66 N/mm\(^2\). The beam has to resist a factored shear force of 440 kN. The spacing of two-legged, 10 mm diameter vertical stirrups of Fe 415 grade steel is ________ mm. (round off to the nearest integer)
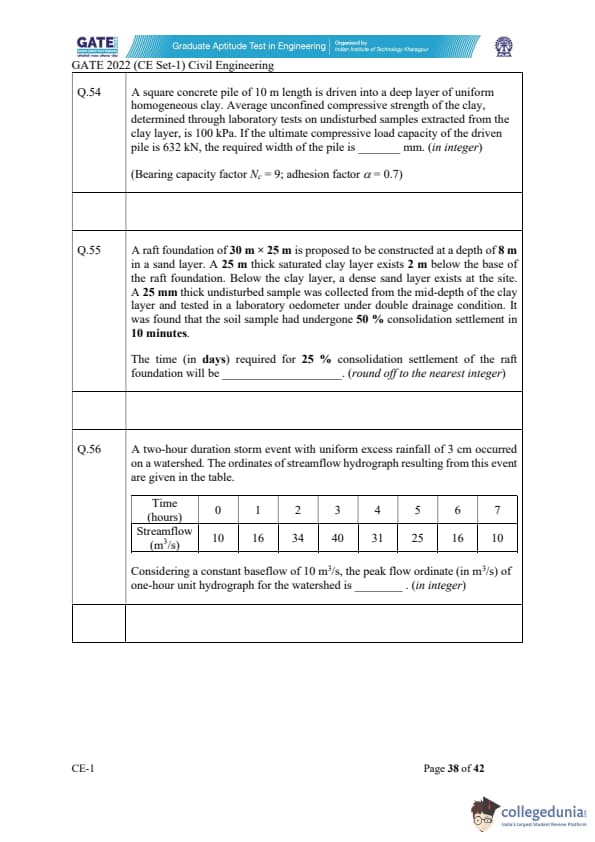
A square concrete pile of 10 m length is driven into a deep layer of uniform homogeneous clay. Average unconfined compressive strength of the clay, determined through laboratory tests on undisturbed samples extracted from the clay layer, is 100 kPa. If the ultimate compressive load capacity of the driven pile is 632 kN, the required width of the pile is ________ mm. (in integer)
(Bearing capacity factor \( N_c = 9 \), adhesion factor \( \alpha = 0.7 \))
A raft foundation of \( 30 \, m \times 25 \, m \) is proposed to be constructed at a depth of 8 m in a sand layer. A 25 mm thick saturated clay layer exists 2 m below the base of the raft foundation. Below the clay layer, a dense sand layer exists at the site. A 25 mm thick undisturbed sample was collected from the mid-depth of the clay layer and tested in a laboratory oedometer under double drainage condition. It was found that the soil sample had undergone 50 % consolidation settlement in 10 minutes.
The time (in days) required for 25 % consolidation settlement of the raft foundation will be ________. (round off to the nearest integer)
A two-hour duration storm event with uniform excess rainfall of 3 cm occurred on a watershed. The ordinates of streamflow hydrograph resulting from this event are given in the table.

Considering a constant baseflow of 10 m\(^3\)/s, the peak flow ordinate (in m\(^3\)/s) of the one-hour unit hydrograph for the watershed is ________. (in integer)
Two reservoirs are connected by two parallel pipes of equal length and of diameters 20 cm and 10 cm, as shown in the figure (not drawn to scale). When the difference in the water levels of the reservoirs is 5 m, the ratio of discharge in the larger diameter pipe to the discharge in the smaller diameter pipe is ________ (round off to two decimal places).

Depth of water flowing in a 3 m wide rectangular channel is 2 m. The channel carries a discharge of 12 m\(^3\)/s. Take \( g = 9.8 \, m/s^2 \). The bed width (in m) at contraction, which just causes the critical flow, is ______ without changing the upstream water level. (round off to two decimal places)
A wastewater sample contains two nitrogen species, namely ammonia and nitrate. Consider the atomic weight of N, H, and O as 14 g/mol, 1 g/mol, and 16 g/mol, respectively. In this wastewater, the concentration of ammonia is 34 mg NH\(_3\)/liter and that of nitrate is 6.2 mg NO\(_3^-\)/liter. The total nitrogen concentration in this wastewater is ____ milligrams nitrogen per liter. (round off to one decimal place)
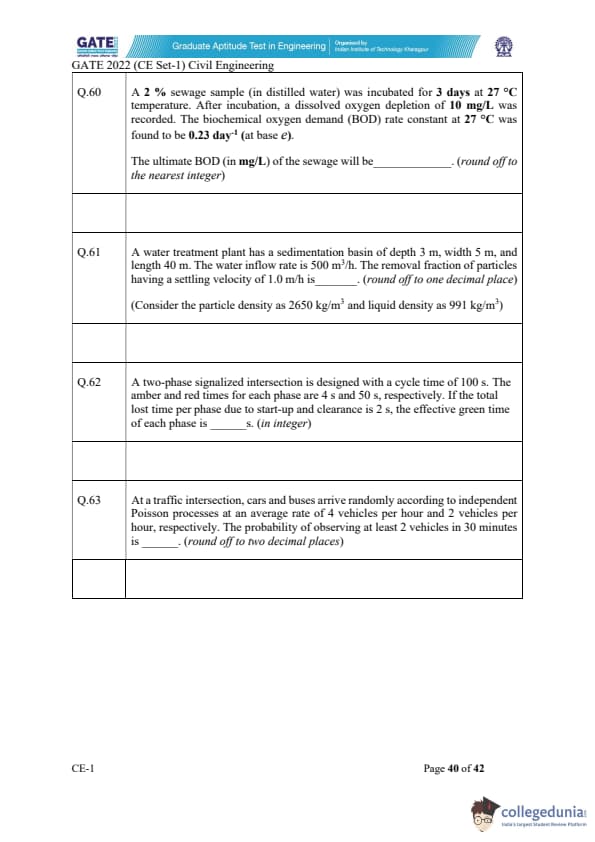
A 2 % sewage sample (in distilled water) was incubated for 3 days at 27 °C temperature. After incubation, a dissolved oxygen depletion of 10 mg/L was recorded. The biochemical oxygen demand (BOD) rate constant at 27 °C was found to be 0.23 day\(^{-1}\) (at base e).
The ultimate BOD (in mg/L) of the sewage will be ________ . (round off to the nearest integer)
A water treatment plant has a sedimentation basin of depth 3 m, width 5 m, and length 40 m. The water inflow rate is 500 m\(^3\)/h. The removal fraction of particles having a settling velocity of 1.0 m/h is ________ . (round off to one decimal place)
(Consider the particle density as 2650 kg/m\(^3\) and liquid density as 991 kg/m\(^3\))
A two-phase signalized intersection is designed with a cycle time of 100 s. The amber and red times for each phase are 4 s and 50 s, respectively. If the total lost time per phase due to start-up and clearance is 2 s, the effective green time of each phase is ________ s. (in integer)
At a traffic intersection, cars and buses arrive randomly according to independent Poisson processes at an average rate of 4 vehicles per hour and 2 vehicles per hour, respectively. The probability of observing at least 2 vehicles in 30 minutes is ________ . (round off to two decimal places)
The vehicle count obtained in every 10 minute interval of a traffic volume survey done in peak one hour is given below.

The peak hour factor (PHF) for 10 minute sub-interval is ______ (round off to one decimal place).
For the dual-wheel carrying assembly shown in the figure, \( P \) is the load on each wheel, \( a \) is the radius of the contact area of the wheel, \( s \) is the spacing between the wheels, and \( d \) is the clear distance between the wheels. Assuming that the ground is an elastic, homogeneous, and isotropic half space, the ratio of Equivalent Single Wheel Load (ESWL) at depth \( z = \frac{d}{2} \) to the ESWL at depth \( z = 2s \) is ______ (round off to one decimal place).

Also Check:































Quick Links:
GATE 2022 CE Slot 1 Detailed Paper Analysis
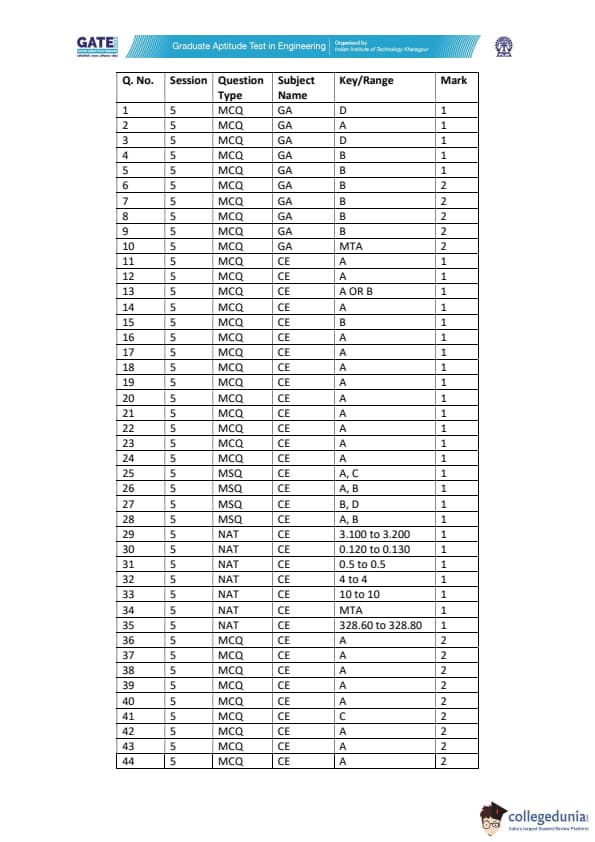
GATE 2022 CE question paper for slot 1 carried 35 MCQs (Multiple Choice Questions), 23 NATs (Numerical Answer Type), and 7 MSQs (Multiple Select Questions). All the questions carried either 1 or 2 marks.
- No questions were asked from the Engineering Mechanics chapter.
- Only 1 question appeared from Design and Steels.
- Irrigation Engineering made a contribution of only 2 questions.
- Environmental Engineering carried the greatest weightage of all the topics in core CE. It carried a total of 8 questions holding 11% of the weightage.
- The Aptitude section was the toughest of all the sections
Go through the below-mentioned table to get the details of the number of questions asked from each chapter:
| Topics/Section | Questions Carrying 1 mark | Questions Carrying 2 marks | Carried Marks |
|---|---|---|---|
| Engineering Mathematics | 3 | 5 | 13 |
| Strength of Materials | 1 | 1 | 3 |
| Engineering Hydrology | - | 1 | 2 |
| Engineering Mechanics | - | - | - |
| Geotechnical Engineering | 5 | 3 | 11 |
| Structural Analysis | - | 3 | 6 |
| Surveying | 2 | 2 | 6 |
| Building Material and Construction Management | 2 | 1 | 4 |
| Design and Steels | 0 | 1 | 2 |
| Irrigation Engineering | 1 | 1 | 3 |
| Transportation Engineering | 2 | 3 | 8 |
| Fluid Mechanics and Hydraulics | 2 | 3 | 8 |
| Environmental Engineering | 5 | 3 | 11 |
| Design of Concrete Structures | 2 | 3 | 8 |
| General Aptitude | 5 | 5 | 15 |
| Total | 30 | 35 | 100 |
Also Check:
GATE Previous Year Question Papers
| GATE 2022 Question Papers | GATE 2021 Question Papers | GATE 2020 Question Papers |
| GATE 2019 Question Papers | GATE 2018 Question Papers | GATE 2017 Question Paper |





Comments