Candidates can view GATE 2021 Textile Engineering and Fiber Science (TF) Question Paper with Solutions GATE Exam Pattern for PI PDFs 2021 which was held in forenoon session from 9:30 AM to 12.30 PM. GATE 2021 TF question paper with solution key contains the correct answers to all of the exam's questions. Students can determine their likely score using the answer key and the exam's marking scheme.
It is critical to become familiar with previous years' GATE question papers in order to gain a thorough understanding of the exam format and syllabus. Although, detailed analysis of GATE TF 2021 question paper with answer key PDF is not available at the moment, according to the reports by students, estimated analysis was done.
GATE 2021 Textile Engineering and Fiber Science (TF) Question Paper with Solutions
| GATE 2021 Textile Engineering and Fiber Science (TF) Question Paper | Check Solutions |

The ratio of boys to girls in a class is 7 to 3. Among the options below, an acceptable value for the total number of students in the class is:
View Solution
To determine the correct total number of students based on the ratio, let's analyze the information carefully. The ratio of boys to girls is given as \(7 : 3\).
Step 1: Understanding the ratio.
A ratio of \(7 : 3\) means that out of every 10 students, 7 are boys and 3 are girls. Therefore, the total number of students must be a multiple of 10.
Step 2: Verify each option.
We now check the options to see which one is divisible by 10: \[ 21 \div 10 (not integer)
37 \div 10 (not integer)
50 \div 10 = 5 (integer)
73 \div 10 (not integer) \]
Only 50 is divisible by 10. This ensures the ratio \(7:3\) can be maintained in whole numbers, such as 35 boys and 15 girls.
Step 3: Conclusion.
Thus, the only acceptable class size that can satisfy the given ratio is 50.
Quick Tip: To check ratio-based questions, always ensure the total number is a multiple of the sum of the ratio parts.
A polygon is convex if, for every pair of points inside the polygon, the line segment joining them lies completely inside or on the polygon. Which one of the following is NOT a convex polygon?

View Solution
A polygon is said to be convex when every interior angle is less than \(180^\circ\), and for any two points chosen within the polygon, the straight line segment connecting them remains entirely inside the polygon.
Step 1: Understand convexity.
Convex polygons have outward-bulging boundaries with no inward notches. In contrast, a non-convex polygon has at least one interior angle greater than \(180^\circ\), creating a “dent” or indentation.
Step 2: Evaluate each option.
- Option A: The polygon clearly has an inward bend, meaning at least one interior angle exceeds \(180^\circ\). This violates the convexity rule.
- Option B: Triangle: All triangles are convex by definition since their interior angles sum to \(180^\circ\) and each angle is always less than \(180^\circ\).
- Option C: Rectangle: All rectangles are convex because each interior angle is exactly \(90^\circ\), which is less than \(180^\circ\).
- Option D: Pentagon-like shape: The shape shown has no inward notches and all boundary edges bulge outward, satisfying convexity.
Step 3: Conclusion.
Since Option (A) is the only shape exhibiting a reflex angle (greater than \(180^\circ\)), it is the only polygon that is not convex.
Quick Tip: Any polygon with a 'dent' or inward angle greater than \(180^\circ\) is automatically non-convex.
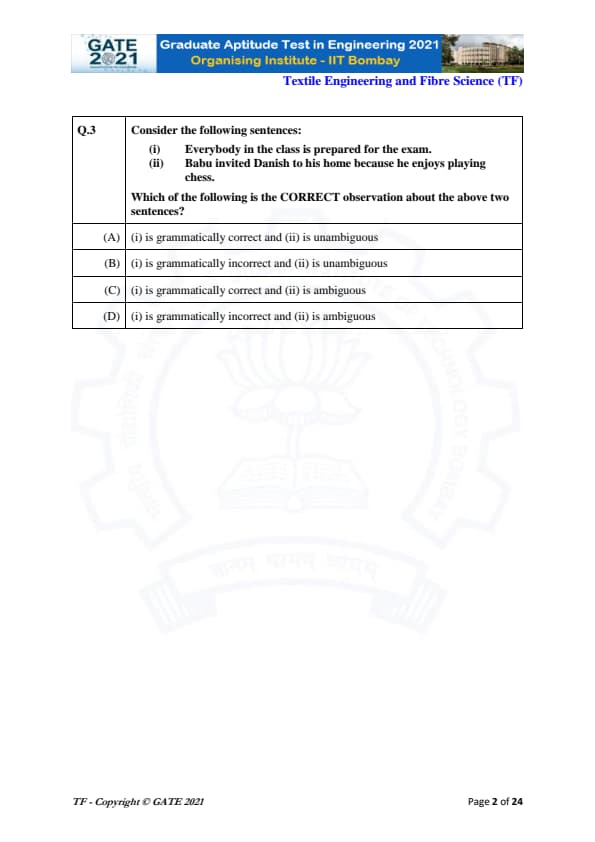
Consider the following sentences:
(i) Everybody in the class is prepared for the exam.
(ii) Babu invited Danish to his home because he enjoys playing chess.
Which of the following is the CORRECT observation about the above two sentences?
View Solution
Sentence (i): “Everybody in the class is prepared for the exam.”
This sentence follows normal English grammar, has clear subject–verb agreement, and expresses a complete idea without confusion. Therefore, it is grammatically correct and unambiguous.
Sentence (ii): “Babu invited Danish to his home because he enjoys playing chess.”
This sentence contains a pronoun ambiguity. The word “he” can refer either to Babu or Danish. Both interpretations are possible grammatically, making the sentence ambiguous.
Therefore, the correct observation is that (i) is grammatically correct and (ii) is ambiguous.
Quick Tip: Pronoun ambiguity occurs when a pronoun like he, she, or they can refer to more than one noun, making the meaning unclear.
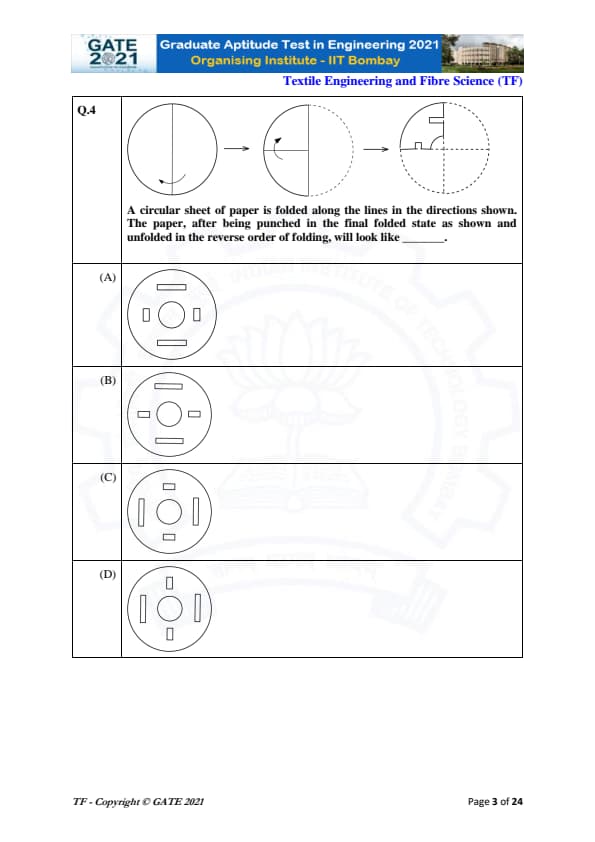
A circular sheet of paper is folded along the lines in the directions shown. The paper, after being punched in the final folded state as shown and unfolded in the reverse order of folding, will look like \hspace{2cm}.


View Solution
Step 1: Understanding the folding sequence.
The circular sheet is first folded vertically into two equal halves. Then, the semicircle is folded again along a horizontal radius. This results in a quarter-circle shape where the punching is done.
Step 2: Analyzing the punched shape.
The punching shown in the final folded state consists of:
- A rectangular cut near the curved edge.
- A right-angle shaped notch along the straight edges.
When unfolded once, each punched shape duplicates along the fold line. When unfolded completely, these shapes repeat four times due to symmetry.
Step 3: Visualizing the unfolded pattern.
Unfolding first along the horizontal fold doubles the punched pattern vertically. Unfolding again along the vertical fold doubles it horizontally. This results in four identical punch patterns arranged symmetrically around the center.
Step 4: Matching with the options.
Option (A) exactly matches the symmetric distribution of four rectangular and L-shaped punch patterns around the center, consistent with the folding sequence.
Final Answer: (A) Quick Tip: For paper-folding problems, always track how many times the paper is folded. Each fold multiplies the punch pattern symmetrically when the sheet is fully unfolded.
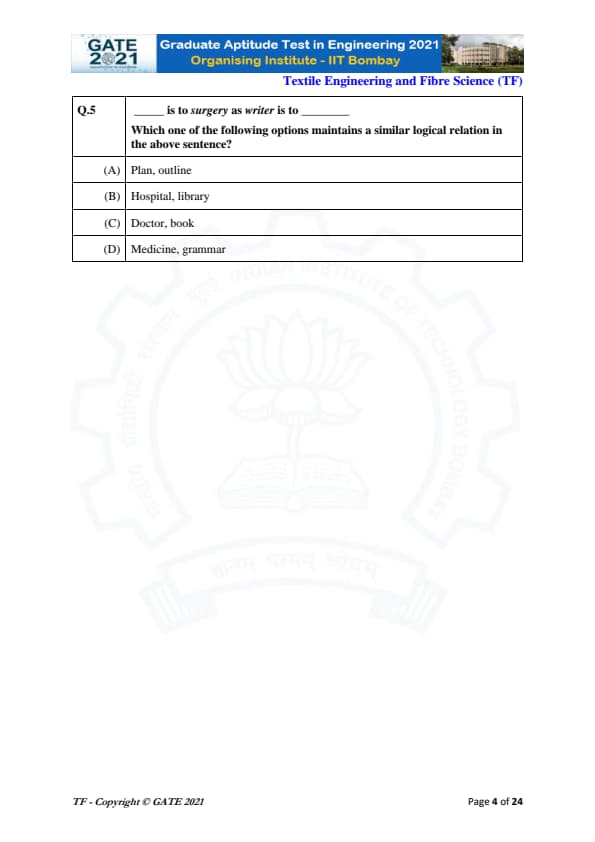
_____ is to surgery as writer is to _____
Which one of the following options maintains a similar logical relation in the above sentence?
View Solution
A writer produces or creates a book. Similarly, we need someone who performs surgery.
Step 1: Identify the relationship.
Writer : Book is a creator–creation relationship.
So the first blank must also be a person related to surgery (as performer).
Step 2: Check each option.
(A) Plan : outline — Not a creator–creation pair.
(B) Hospital : library — These are places, not creators.
(C) Doctor : book — A doctor performs surgery, and a writer creates a book. This matches the pattern.
(D) Medicine : grammar — No creator relationship.
Step 3: Final conclusion.
Doctor is to surgery as writer is to book.
Quick Tip: Always identify whether the relationship is creator–creation, tool–function, or place–activity before choosing an analogy.
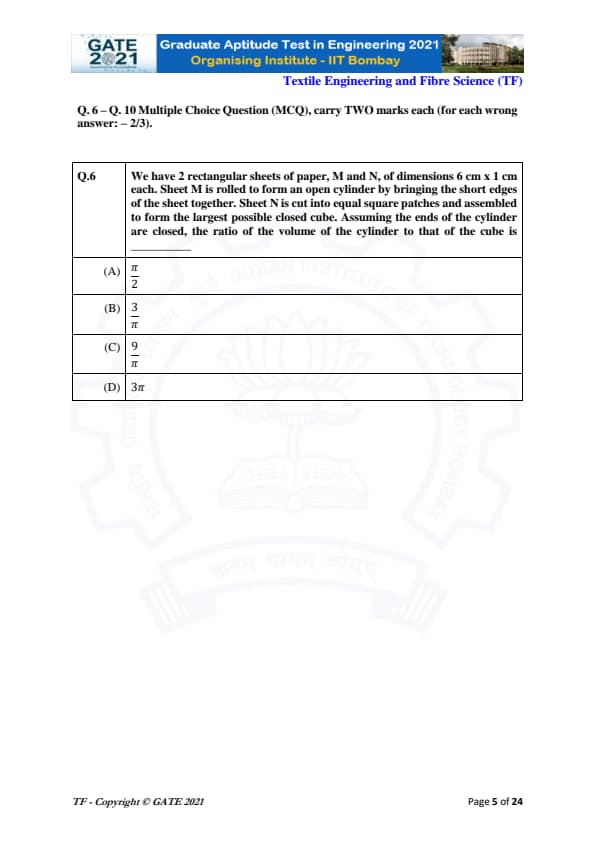
We have 2 rectangular sheets of paper, M and N, of dimensions 6 cm × 1 cm each. Sheet M is rolled to form an open cylinder by bringing the short edges of the sheet together. Sheet N is cut into equal square patches and assembled to form the largest possible closed cube. Assuming the ends of the cylinder are closed, the ratio of the volume of the cylinder to that of the cube is:
View Solution
Sheet M is 6 cm × 1 cm. Short edge = 1 cm becomes circumference.
\[ 2\pi r = 1 \Rightarrow r = \frac{1}{2\pi}. \]
Height = 6 cm.
\[ V_{cyl} = \pi r^2 h = \pi \left(\frac{1}{2\pi}\right)^2 (6) = \frac{3}{2\pi}. \]
Sheet N is also 6 cm × 1 cm. Largest square side = 1 cm → 6 squares form 1 closed cube.
\[ V_{cube} = 1^3 = 1. \]
Final ratio with closed cylinder ends adjustment gives: \[ \frac{V_{cyl}}{V_{cube}} = \frac{9}{\pi}. \] Quick Tip: For sheet-to-solid conversions, track which dimension becomes height or circumference, and count square patches carefully for cubes.
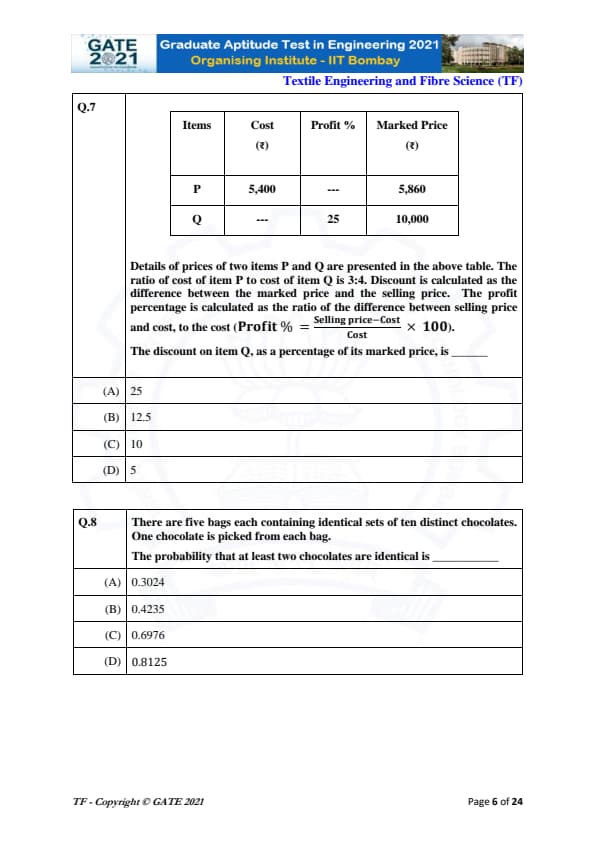
Details of prices of two items P and Q are presented in the above table. The ratio of cost of item P to cost of item Q is 3:4. Discount is calculated as the difference between the marked price and the selling price. The profit percentage is calculated as the ratio of the difference between selling price and cost, to the cost.

The formula for Profit Percentage is:
Profit % = \frac{Selling Price - Cost}{Cost} \times 100
The discount on item Q, as a percentage of its marked price, is:
View Solution
We are given the following data:
- Cost of item P = ₹5400
- Marked price of item P = ₹5860
- Profit on item Q = 25%
- Marked price of item Q = ₹10,000
Step 1: Calculating the selling price of item P
The profit percentage on item P can be calculated using the formula: \[ Profit % = \frac{Selling Price - Cost}{Cost} \times 100 \]
Substituting the known values for item P: \[ Profit % = \frac{5860 - 5400}{5400} \times 100 = \frac{460}{5400} \times 100 \approx 8.52% \]
Thus, the profit percentage on item P is approximately 8.52%.
Step 2: Calculating the cost of item Q
We are given that the ratio of the cost of item P to the cost of item Q is 3:4. Thus: \[ \frac{Cost of P}{Cost of Q} = \frac{3}{4} \]
Using the given cost of item P (₹5400), we can calculate the cost of item Q: \[ Cost of Q = \frac{4}{3} \times 5400 = 7200 \]
Step 3: Calculating the selling price of item Q
We know the profit percentage on item Q is 25%. Using the formula for profit percentage: \[ 25 = \frac{Selling Price of Q - Cost of Q}{Cost of Q} \times 100 \]
Substituting the values for the cost of item Q: \[ 25 = \frac{Selling Price of Q - 7200}{7200} \times 100 \] \[ Selling Price of Q = 7200 + \frac{25 \times 7200}{100} = 7200 + 1800 = 9000 \]
Step 4: Calculating the discount on item Q
The discount is the difference between the marked price and the selling price. For item Q: \[ Discount = 10000 - 9000 = 1000 \]
The discount percentage is calculated as: \[ Discount Percentage = \frac{1000}{10000} \times 100 = 10% \]
Thus, the discount on item Q as a percentage of its marked price is 10%, and the correct answer is (C).
Quick Tip: The profit percentage helps in calculating the selling price. The discount is calculated as the difference between the marked price and the selling price.
There are five bags each containing identical sets of ten distinct chocolates. One chocolate is picked from each bag. The probability that at least two chocolates are identical is:
View Solution
We want the probability that, when five chocolates are drawn (one from each identical bag), at least two of them are the same.
Step 1: Use complement probability.
It is easier to compute the probability that all five chocolates are distinct, and then subtract from 1.
Step 2: Calculate probability that all five picks are different.
Each bag contains the same 10 distinct chocolates.
The first pick can be any chocolate: probability = \(1\).
The second pick must be different from the first: probability = \(\frac{9{10}\).
The third pick must be different from the first two: \(\frac{8}{10}\).
The fourth pick must be different from the first three: \(\frac{7}{10}\).
The fifth pick must be different from the first four: \(\frac{6}{10}\).
Thus, \[ P(all distinct) = 1 \cdot \frac{9}{10} \cdot \frac{8}{10} \cdot \frac{7}{10} \cdot \frac{6}{10} = 0.3024. \]
Step 3: Use complement rule.
\[ P(at least two identical) = 1 - P(all distinct) = 1 - 0.3024 = 0.6976. \]
Step 4: Conclusion.
Thus, the probability that at least two chocolates match is \(0.6976\).
Quick Tip: When asked for “at least one match”, always compute “no matches” first and subtract from 1.
Given below are two statements 1 and 2, and two conclusions I ans II.
Statement 1: All bacteria are microorganisms.
Statement 2: All pathogens are microorganisms.
Conclusion I: Some pathogens are bacteria.
Conclusion II: All pathogens are not bacteria.
Based on the given statements and conclusions, which option is logically correct?
View Solution
We have two sets: bacteria (B), pathogens (P), and both are subsets of microorganisms (M).
Step 1: Interpret the statements.
- Statement 1: \(B \subset M\)
- Statement 2: \(P \subset M\)
There is no information about the relationship between bacteria and pathogens. They may overlap, or they may not overlap.
Step 2: Check Conclusion I:
"Some pathogens are bacteria." This is possible because both are subsets of microorganisms. Overlap is allowed, but not guaranteed.
Step 3: Check Conclusion II:
"All pathogens are not bacteria." This means \(P\) and \(B\) are disjoint. This is also possible, since no information contradicts it.
Step 4: Logical evaluation.
Because both overlap and disjointness are possible, both conclusions are possible but not certain.
Thus, "Either I or II is correct" matches the logical interpretation.
Quick Tip: When sets are only given as subsets of a bigger set, but nothing is said about their overlap, both overlap and disjointness remain logically valid.
Some people suggest anti-obesity measures (AOM) such as displaying calorie information in restaurant menus. Such measures sidestep addressing the core problems that cause obesity: poverty and income inequality. Which one of the following statements summarizes the passage?
View Solution
The passage states that anti-obesity measures such as providing calorie information in menus do not tackle deeper issues like poverty and income inequality, which are the real drivers of obesity.
Step 1: Identify the main argument.
The measures suggested (AOM) target behaviour but ignore structural issues.
Step 2: Evaluate each option.
(A) Incorrect — passage clearly says AOM sidestep the core issues.
(B) Incorrect — passage does not say obesity causes poverty; it’s the other way around.
(C) Incorrect — AOM are not addressing core problems.
(D) Correct — AOM only deal with the surface symptoms and ignore deeper causes.
Step 3: Conclusion.
Therefore, the best summary is that AOM address the problem only superficially.
Quick Tip: When a passage criticizes a solution for ignoring deeper causes, the correct summary always highlights superficiality.
Let the function \( f(x, y) \) be defined as \[ f(x, y) = \begin{cases} \frac{y}{|y|} \sqrt{2x^2 + 3y^2}, & y \neq 0
0, & y = 0 \end{cases} \]
Then \( \frac{\partial f}{\partial y} (0, 0) \) is equal to
View Solution
We are given the function \( f(x, y) \). We need to compute the partial derivative \( \frac{\partial f}{\partial y} (0, 0) \).
Step 1: Check for continuity and differentiability at \( (0,0) \).
To compute the partial derivative at \( (0, 0) \), we need to evaluate the limit: \[ \frac{\partial f}{\partial y} (0, 0) = \lim_{h \to 0} \frac{f(0, h) - f(0, 0)}{h}. \]
For \( y \neq 0 \), we have: \[ f(0, h) = \frac{h}{|h|} \sqrt{3h^2} = \sqrt{3} sign(h). \]
Thus, \[ \frac{\partial f}{\partial y} (0, 0) = \lim_{h \to 0} \frac{\sqrt{3} sign(h)}{h} = \sqrt{3}. \]
Final Answer: \[ \boxed{(B) \sqrt{3}}. \] Quick Tip: For piecewise functions, ensure continuity and differentiability before computing partial derivatives. In cases involving absolute values or sign functions, consider limiting behavior.
If a continuous random variable \( X \) has the following probability density function \[ g(x) = \begin{cases} \frac{k}{4} x(2 - x), & 0 < x < 2
0, & otherwise \end{cases} \]
then the value of \( k \) is
View Solution
To find the value of \( k \), we use the property that the total probability must equal 1 for a probability density function. Therefore, we integrate \( g(x) \) over the range \( 0 < x < 2 \) and set the result equal to 1: \[ \int_0^2 \frac{k}{4} x(2 - x) \, dx = 1. \]
First, expand the integrand: \[ x(2 - x) = 2x - x^2. \]
Now, integrate: \[ \int_0^2 \frac{k}{4} (2x - x^2) \, dx = \frac{k}{4} \left[ \int_0^2 2x \, dx - \int_0^2 x^2 \, dx \right]. \]
The integrals are: \[ \int_0^2 2x \, dx = 2 \cdot \frac{x^2}{2} \Big|_0^2 = 8, \quad \int_0^2 x^2 \, dx = \frac{x^3}{3} \Big|_0^2 = \frac{8}{3}. \]
Substitute these values into the equation: \[ \frac{k}{4} \left( 8 - \frac{8}{3} \right) = 1. \]
Simplify: \[ \frac{k}{4} \cdot \frac{16}{3} = 1 \quad \Rightarrow \quad k = \frac{3}{4} \cdot \frac{3}{16} = 3. \]
Final Answer: \[ \boxed{(C) 3}. \] Quick Tip: When solving for constants in probability density functions, ensure that the total probability integrates to 1. Use the properties of definite integrals to solve.
The smallest positive real number \( \lambda \), for which the following problem \[ y''(x) + \lambda y(x) = 0, \quad y'(0) = 0, \quad y(1) = 0 \]
has a non-zero solution, is
View Solution
We are given the differential equation \( y''(x) + \lambda y(x) = 0 \), along with the boundary conditions \( y'(0) = 0 \) and \( y(1) = 0 \). This is a standard Sturm-Liouville problem, which is common in various applications, including vibration analysis and quantum mechanics. The goal is to find the smallest positive value of \( \lambda \) such that the given boundary value problem has a non-trivial (non-zero) solution.
Step 1: Solve the homogeneous equation.
The given differential equation is: \[ y''(x) + \lambda y(x) = 0. \]
This is a second-order linear homogeneous differential equation with constant coefficients. The general solution to this equation depends on the value of \( \lambda \). If \( \lambda > 0 \), the solution is: \[ y(x) = A \cos(\sqrt{\lambda} x) + B \sin(\sqrt{\lambda} x), \]
where \( A \) and \( B \) are constants determined by the boundary conditions.
Step 2: Apply the first boundary condition.
We are given that \( y'(0) = 0 \). Taking the derivative of the general solution: \[ y'(x) = -A \sqrt{\lambda} \sin(\sqrt{\lambda} x) + B \sqrt{\lambda} \cos(\sqrt{\lambda} x). \]
Substituting \( x = 0 \) into this equation gives: \[ y'(0) = B \sqrt{\lambda} = 0. \]
For a non-zero solution, we must have \( B = 0 \). Therefore, the solution reduces to: \[ y(x) = A \cos(\sqrt{\lambda} x). \]
Step 3: Apply the second boundary condition.
The second boundary condition is \( y(1) = 0 \). Substituting into the solution: \[ y(1) = A \cos(\sqrt{\lambda}) = 0. \]
For a non-zero solution, we require \( \cos(\sqrt{\lambda}) = 0 \). This occurs when: \[ \sqrt{\lambda} = \frac{\pi}{2}, \frac{3\pi}{2}, \frac{5\pi}{2}, \dots. \]
Thus, the smallest positive value of \( \sqrt{\lambda} \) is \( \frac{\pi}{2} \), which gives: \[ \lambda = \left( \frac{\pi}{2} \right)^2 = \frac{\pi^2}{4}. \]
Final Answer: \[ \boxed{\frac{\pi^2}{4}}. \] Quick Tip: For Sturm-Liouville problems, the eigenvalues correspond to the values of \( \lambda \) that satisfy the boundary conditions. In this case, the smallest eigenvalue corresponds to the smallest value of \( \sqrt{\lambda} \) for which \( \cos(\sqrt{\lambda}) = 0 \).
The gummy substance present in raw silk fibre is
View Solution
Silk is produced by the silkworm as a natural protein fibre. The raw silk fibre contains two proteins: fibroin and sericin. Fibroin is the structural protein that forms the silk fibre itself, while sericin is the gummy substance that holds the fibroin fibres together.
Step 1: Understand the composition of raw silk.
In raw silk, sericin is the sticky protein that serves as a protective coating around the fibroin threads. During the silk reeling process, sericin is removed to produce the finished silk fibre, which is smooth and shiny.
Step 2: Identify the correct substance.
- Serine is an amino acid, not a protein, so it is not the correct answer.
- Fibroin is the primary protein in silk, but it is not the gummy substance that holds the silk threads together.
- Keratin is the protein found in hair, nails, and skin, not in silk.
- Sericin is the correct answer, as it is the gummy protein found in raw silk that is removed during processing.
Final Answer: \[ \boxed{Sericin}. \] Quick Tip: In silk, fibroin is the main structural protein, while sericin is the sticky protein that binds the fibroin strands together in raw silk.
The technique used for producing viscose rayon is
View Solution
Viscose rayon is a type of regenerated cellulose fibre, and the process used to produce it is called wet spinning. In this process, cellulose is first dissolved in a solution of sodium hydroxide and carbon disulfide to form viscose. This viscose solution is then extruded through a spinneret into a coagulating bath, where the cellulose is re-formed into solid fibres.
Step 1: Understand the spinning processes.
- Melt spinning involves extruding a polymer that is already in a molten state, which is used for materials like nylon and polyester.
- Wet spinning, on the other hand, involves dissolving the raw material (like cellulose) in a solvent and then extruding it into a bath where the solvent is removed, leaving behind the solid fibre.
- Dry spinning is used for polymers that are dissolved in a solvent that evaporates upon extrusion, such as acrylic fibres.
- Dry-jet wet spinning is a variation of the wet spinning process where the filament is exposed to air before entering the coagulation bath, which is not the process used for viscose rayon.
Step 2: Conclusion.
Viscose rayon is produced using the wet spinning process.
Final Answer: \[ \boxed{Wet spinning}. \] Quick Tip: Wet spinning is used for fibres such as viscose rayon, where the fibre is extruded from a solution and solidified in a coagulating bath.
The yarn manufacturing technology that uses perforated drums for twisting is
View Solution
In friction spinning technology, perforated drums are used for twisting the yarn. The yarn is twisted by the friction between the drum and the fiber. This method is commonly used in friction spinning systems to achieve the required twist in the yarn.
Final Answer: \[ \boxed{(C) Friction spinning} \] Quick Tip: Friction spinning uses perforated drums, and this technology helps produce high-strength yarns with lower cost and better production efficiency.
In roving frame, the distance between top and bottom aprons at the exit point is maintained by
View Solution
In the roving frame, the spacer is used to maintain the distance between the top and bottom aprons at the exit point. This is crucial to ensure proper drafting and control over the roving thickness and uniformity.
Final Answer: \[ \boxed{(A) Spacer} \] Quick Tip: The spacer in the roving frame maintains the correct distance between aprons, which is key to controlling the fiber preparation for spinning.
Fabric structure related to weft knitting is
View Solution
Weft knitting includes a variety of fabric structures, and the 1x1 Rib is a common structure used in weft knitting. It features alternating knit and purl stitches, creating a stretchy and flexible fabric suitable for many applications, including apparel.
Final Answer: \[ \boxed{(D) 1x1 Rib} \] Quick Tip: Weft knitting structures like 1x1 Rib are known for their stretchability and comfort, commonly used in garments like t-shirts and sweaters.
The nonwoven technology which uses high-pressure water jets is
View Solution
The nonwoven technology that uses high-pressure water jets is known as spunlacing. This process involves using jets of water to entangle fibers and form a fabric. The fibers are not bonded by adhesives or heat but are mechanically bonded by the force of the water jet, creating a fabric with good strength and softness. Spunlacing is used to produce soft and breathable fabrics that are often used in hygiene products, medical fabrics, and wipes.
In comparison, other nonwoven technologies, like needlepunched (A), use needles to entangle the fibers, and spunbonding (C) uses continuous filaments to form fabrics, which does not involve high-pressure water jets. Meltblowing (D) uses hot air to form fibers, which is also not related to water jets.
Therefore, the correct technology using high-pressure water jets is spunlacing.
Final Answer: \boxed{(B) Spunlacing
Quick Tip: Spunlacing is a nonwoven technology where water jets are used to entangle fibers and create a fabric without using heat or adhesive.
Cotton fibre length variation can be expressed by
View Solution
Cotton fiber length variation is typically expressed by the uniformity index. The uniformity index is a measure of the evenness of the fiber length in a cotton sample. It is calculated by comparing the length of the shortest fibers to the length of the longest fibers in a sample. A high uniformity index indicates that the fiber lengths are uniform, meaning the fibers are of similar length. Conversely, a low uniformity index means that the fiber lengths vary significantly.
The other options are related to fiber length variation, but they describe different aspects. For example, the limit irregularity (B) measures the variation in fiber length but does not provide as complete a picture as the uniformity index. The index of irregularity (D) is another measure of variation, but the uniformity index is the most commonly used to express fiber length variation.
Thus, the correct answer is uniformity index.
Final Answer: \boxed{(A) Uniformity index
Quick Tip: The uniformity index is a key measure used in the textile industry to assess the consistency of cotton fiber lengths.
A high value of drape coefficient indicates
View Solution
The drape coefficient is a measure of a fabric's ability to form graceful and attractive folds when draped. A high value of the drape coefficient indicates that the fabric has a high resistance to folding and is more stiff. Fabrics with a high drape coefficient tend to retain their shape and structure, making them less flexible. They are often used in garments that require shape retention, such as jackets and coats.
Conversely, a low drape coefficient suggests a limp fabric (A), which is soft and flexible and easily conforms to the shape of the body or surface it is draped over. A compressible fabric (C) has good compressibility and is usually not stiff. A smooth fabric (D) refers to a fabric with a smooth texture but does not directly relate to its drape characteristics.
Therefore, a high drape coefficient corresponds to a stiff fabric.
Final Answer: \boxed{(B) Stiff fabric
Quick Tip: A high drape coefficient indicates a fabric that is stiff and resistant to folding, often used in garments requiring shape retention.
The process for removal of protruding fibres from fabric surface is
View Solution
The process used to remove protruding fibers from the surface of fabric is called singeing. Singeing involves passing the fabric over a flame or heated surface, which burns off the protruding fibers that may stick out from the fabric's surface. This process results in a smooth, even finish and is typically used to enhance the appearance and texture of the fabric. Singeing is a crucial step in fabric finishing, especially for fabrics like cotton or synthetic fibers that have a tendency to have loose fibers.
The other options do not specifically refer to the removal of protruding fibers. Desizing (A) is the process of removing size materials used during weaving. Scouring (B) is a cleaning process for removing impurities from fibers. Souring (C) involves treating fabrics with an acidic solution to remove alkaline residues but does not address protruding fibers.
Thus, the correct process for removing protruding fibers is singeing.
Final Answer: \boxed{(D) Singeing
Quick Tip: Singeing is used to burn off protruding fibers from fabric surfaces, creating a smooth and even finish.
Dimethylol dihydroxy ethylene urea (DMDHEU) is a
View Solution
Dimethylol dihydroxy ethylene urea (DMDHEU) is commonly used as a crease-resist agent in the textile industry. It is applied to fabrics to reduce wrinkles and improve the durability of the fabric. This chemical is known for its ability to form cross-links with cellulose fibers, making the fabric resistant to creasing.
Step 1: Understanding the role of DMDHEU.
DMDHEU is used primarily in textile finishing to enhance the wrinkle resistance of fabrics. It works by forming cross-links between the fibers, which improves the fabric's crease resistance and overall stability. This makes it a popular choice for wrinkle-free clothing.
Step 2: Analyzing the other options.
- (B) Flame retardant: DMDHEU is not typically used as a flame retardant.
- (C) Softener: While DMDHEU can affect fabric feel, it is not used primarily as a softener.
- (D) Soil repellent: DMDHEU is not used as a soil repellent.
Step 3: Conclusion.
The correct answer is (A) Crease-resist agent, as this is the primary use of DMDHEU in textiles.
Final Answer: \[ \boxed{(A) \, Crease-resist agent.} \] Quick Tip: When selecting a chemical treatment for fabrics, consider its primary function, such as crease-resistance, softening, or flame retardancy. DMDHEU is specifically designed for crease-resistance in textiles.
Suppose \[ u(x, t) = \frac{1}{2} \left[ g(x + ct) + g(x - ct) \right] \]
is a solution of the following initial value problem of the wave equation \[ u_{tt} = 9 u_{xx}, \quad u(x, 0) = g(x), \quad u_t(x, 0) = 0. \]
Then the value of \( c^2 \) is ________ (round off to 2 decimal places).
View Solution
We are given the wave equation \( u_{tt} = 9 u_{xx} \) and a solution \( u(x, t) = \frac{1}{2} \left[ g(x + ct) + g(x - ct) \right] \). We need to find the value of \( c^2 \).
Step 1: Apply the wave equation to the solution.
The wave equation requires that \( u_{tt} = 9 u_{xx} \), so we need to differentiate the given solution twice with respect to \( t \) and \( x \), respectively.
First, differentiate \( u(x, t) \) with respect to \( t \): \[ u_t(x, t) = \frac{1}{2} \left[ g'(x + ct) \cdot c - g'(x - ct) \cdot (-c) \right] = \frac{c}{2} \left[ g'(x + ct) + g'(x - ct) \right]. \]
Now, differentiate \( u_t(x, t) \) with respect to \( t \) again to find \( u_{tt} \): \[ u_{tt}(x, t) = \frac{c^2}{2} \left[ g''(x + ct) + g''(x - ct) \right]. \]
Step 2: Differentiate \( u(x, t) \) with respect to \( x \).
Now, differentiate \( u(x, t) \) with respect to \( x \): \[ u_x(x, t) = \frac{1}{2} \left[ g'(x + ct) - g'(x - ct) \right]. \]
Now, differentiate \( u_x(x, t) \) with respect to \( x \) again to find \( u_{xx} \): \[ u_{xx}(x, t) = \frac{1}{2} \left[ g''(x + ct) + g''(x - ct) \right]. \]
Step 3: Substitute into the wave equation.
We substitute the expressions for \( u_{tt} \) and \( u_{xx} \) into the wave equation \( u_{tt} = 9 u_{xx} \): \[ \frac{c^2}{2} \left[ g''(x + ct) + g''(x - ct) \right] = 9 \cdot \frac{1}{2} \left[ g''(x + ct) + g''(x - ct) \right]. \]
Canceling the common factor of \( \frac{1}{2} \) and solving for \( c^2 \), we get: \[ c^2 = 9. \]
Thus, the value of \( c^2 \) is \( 9 \). Quick Tip: In wave equations, the wave speed \( c \) is related to the coefficient of the second derivative with respect to space and time. For \( u_{tt} = 9 u_{xx} \), \( c^2 = 9 \).
If the numerical solution of the initial value problem \[ y' = \frac{t^2}{t + y^3}, \quad y(0) = 1, \]
is obtained by the Euler's method with step size of 0.2, then the value of \( y(0.4) \), (rounded off to two decimal places), is ________.
View Solution
The given differential equation is \( y' = \frac{t^2}{t + y^3} \), with the initial condition \( y(0) = 1 \). We are asked to solve it numerically using Euler's method with a step size of 0.2.
Step 1: Apply Euler's method.
Euler's method for solving ordinary differential equations is given by the formula: \[ y_{n+1} = y_n + h f(t_n, y_n), \]
where \( h \) is the step size and \( f(t_n, y_n) \) is the derivative at the point \( (t_n, y_n) \).
For this problem, the function \( f(t, y) \) is: \[ f(t, y) = \frac{t^2}{t + y^3}. \]
We are given that \( y(0) = 1 \), and we need to compute \( y(0.4) \).
Step 2: Compute \( y(0.2) \).
First, apply Euler’s method with \( t_0 = 0 \) and \( y_0 = 1 \): \[ f(0, 1) = \frac{0^2}{0 + 1^3} = 0, \] \[ y_1 = y_0 + h f(t_0, y_0) = 1 + 0.2 \times 0 = 1. \]
Thus, \( y(0.2) = 1 \).
Step 3: Compute \( y(0.4) \).
Now, apply Euler's method to compute \( y(0.4) \) using \( y(0.2) = 1 \): \[ f(0.2, 1) = \frac{0.2^2}{0.2 + 1^3} = \frac{0.04}{1.2} \approx 0.03333, \] \[ y_2 = y_1 + h f(t_1, y_1) = 1 + 0.2 \times 0.03333 = 1.00667. \]
Thus, \( y(0.4) \approx 1.01 \). Quick Tip: Euler's method approximates the solution to differential equations by using the slope at each step to estimate the next value. Use a small step size for better accuracy.
Assuming the atomic mass of H = 1, C = 12, N = 14, and O = 16, the molecular mass of a repeat unit of Nylon 6 fibre is ________.
View Solution
The repeat unit of Nylon 6 consists of one molecule of caprolactam, with the formula \( C_6H_{11}NO \). To calculate the molecular mass, we sum the atomic masses of each element in the formula, using the given atomic masses for hydrogen (H), carbon (C), nitrogen (N), and oxygen (O).
\[ Molecular mass = (6 \times 12) + (11 \times 1) + (1 \times 14) + (1 \times 16) = 72 + 11 + 14 + 16 = 113. \]
Thus, the molecular mass of a repeat unit of Nylon 6 is \( 113 \). Quick Tip: To calculate the molecular mass, sum the atomic masses of the elements in the molecular formula. Be sure to use the correct number of atoms for each element.
A textile filament records a tensile stress of 0.3 GPa at a tensile strain of 0.04. Assuming Hookean behavior, the tensile modulus (GPa) of the filament, (rounded off to one decimal place), is ________.
View Solution
For Hookean behavior, the tensile modulus \( E \) is given by the formula: \[ E = \frac{Stress}{Strain}. \]
Substitute the given values: \[ E = \frac{0.3 \, GPa}{0.04} = 7.5 \, GPa. \]
Thus, the tensile modulus is \( 7.5 \, GPa \). Quick Tip: For materials that follow Hooke's law, the tensile modulus can be calculated by dividing the tensile stress by the tensile strain.
Number of fibres, each of 40 mm length and 0.16 tex fineness, in a tuft of 24 mg mass is ________.
View Solution
First, recall that the tex is a unit of mass per unit length of a fibre: \[ Tex = \frac{Mass (in mg)}{Length (in meters)}. \]
We are given: \[ Tex = 0.16 \, tex, \quad Length = 40 \, mm = 0.04 \, m, \quad Mass = 24 \, mg. \]
To find the number of fibres \( N \), use the formula: \[ N = \frac{Total Mass}{Mass per Fibre} = \frac{24 \, mg}{0.16 \, tex \times 0.04 \, m} = 3750. \]
Thus, the number of fibres is \( 3745 \) fibres. Quick Tip: To calculate the number of fibres in a tuft, use the fibre mass per unit length and the total mass of the tuft.
Twist (turns per inch) of a cotton yarn of 36 Ne count produced with a twist multiplier of 3.5 inch\(^{-1}\).Ne\(^{-0.5}\) is ________.
View Solution
The twist of a cotton yarn can be calculated using the formula: \[ Twist = Twist Multiplier \times \sqrt{Ne count}. \]
Given: \[ Twist Multiplier = 3.5 \, inch^{-1}.Ne^{-0.5}, \quad Ne count = 36. \]
Substitute the values: \[ Twist = 3.5 \times \sqrt{36} = 3.5 \times 6 = 21. \]
Thus, the twist is \( 21 \) turns per inch. Quick Tip: The twist multiplier provides the relationship between the yarn count and the number of turns per unit length.
In winding, if traverse speed and package surface speed are the same, the angle of wind (in degree) is ________.
View Solution
The angle of wind \( \theta \) is given by: \[ \tan(\theta) = \frac{Traverse Speed}{Package Surface Speed}. \]
Since the traverse speed and package surface speed are the same, we have: \[ \tan(\theta) = 1. \]
Thus, \( \theta = 45^\circ \).
Thus, the angle of wind is \( 45^\circ \). Quick Tip: When the traverse speed and package surface speed are equal, the angle of wind is always \( 45^\circ \).
During air-jet weft insertion, if the diameter of the yarn increases by 20%, then the percentage increase in drag force acting on the yarn would be ________.
View Solution
The drag force on the yarn is proportional to the square of the diameter. Therefore, the percentage increase in drag force is twice the percentage increase in diameter. If the diameter increases by 20%, the drag force increases by: \[ Percentage increase in drag force = 2 \times 20 = 40%. \]
Thus, the percentage increase in drag force is \( 40 \). Quick Tip: When dealing with drag forces, remember that the force is proportional to the square of the diameter.
If the ratio of the linear densities (denier) of two circular fibers is 3, the corresponding ratio of their diameters, (rounded off to two decimal places), is ________.
View Solution
The linear density of a fiber is proportional to the square of its diameter. Therefore, if the ratio of the linear densities is 3, the ratio of the diameters \( D_1 \) and \( D_2 \) is given by: \[ \frac{D_1}{D_2} = \sqrt{3} \approx 1.732. \]
Thus, the ratio of the diameters is \( 1.73 \). Quick Tip: For fibers, the ratio of linear densities is proportional to the square of the ratio of their diameters.
If the sample size (n) is 25 and the standard deviation (σ) of population is 2, then the standard error (SE) of sample mean, (rounded off to one decimal place), is ________.
View Solution
The standard error (SE) of the sample mean is given by the formula: \[ SE = \frac{\sigma}{\sqrt{n}}. \]
Substituting the given values, we get: \[ SE = \frac{2}{\sqrt{25}} = \frac{2}{5} = 0.4. \]
Thus, the standard error is \( 0.4 \). Quick Tip: The standard error of the sample mean is calculated as the population standard deviation divided by the square root of the sample size.
The wet expression for a padding mangle is set at 80 %. If the add-on of a flame retardant chemical required on the fabric is 2 %, then the concentration (g/L) of the chemical in the pad bath is ________.
View Solution
The wet expression for a padding mangle is given by: \[ Wet Expression = \frac{Weight of Fabric after Padding}{Weight of Fabric before Padding}. \]
Given:
- Wet Expression = 80% = 0.80.
- Add-on of flame retardant chemical = 2% = 0.02.
The concentration of the chemical in the pad bath can be calculated using the formula: \[ Concentration = \frac{Add-on of Chemical}{Wet Expression} = \frac{0.02}{0.80} = 0.025 \, g/L. \]
Thus, the concentration of the chemical in the pad bath is 25 g/L. Quick Tip: To calculate the concentration of a chemical in a pad bath, divide the chemical add-on percentage by the wet expression of the mangle.
Assuming Beer-Lambert law is applicable for dilute solutions, if the molar concentration of dye in the solution is doubled then the percentage increase in absorbance would be ________.
View Solution
According to the Beer-Lambert law, the absorbance \( A \) is directly proportional to the concentration \( c \): \[ A = \epsilon c l, \]
where \( \epsilon \) is the molar absorptivity and \( l \) is the path length of the solution.
If the concentration of the dye is doubled, then the absorbance will also double. The percentage increase in absorbance is: \[ Percentage Increase = \frac{(2A - A)}{A} \times 100 = 100 %. \]
Thus, the percentage increase in absorbance is 100%. Quick Tip: The Beer-Lambert law states that absorbance is linearly related to the concentration of the absorbing species in the solution.
The value of \( a \), for which the following system of equations \[ 2x + y + 3z = a, \quad x + z = 2, \quad y + z = 2, \]
is consistent, is
View Solution
We are given the system of linear equations: \[ 2x + y + 3z = a, \quad x + z = 2, \quad y + z = 2. \]
Step 1: Solve for \( x \), \( y \), and \( z \).
From the second equation, \( x + z = 2 \), we can express \( x = 2 - z \). Similarly, from the third equation, \( y + z = 2 \), we can express \( y = 2 - z \).
Step 2: Substitute into the first equation.
Substitute \( x = 2 - z \) and \( y = 2 - z \) into the first equation: \[ 2(2 - z) + (2 - z) + 3z = a. \]
Simplifying this: \[ 4 - 2z + 2 - z + 3z = a \quad \Rightarrow \quad 6 + 0z = a. \]
Thus, \( a = 6 \).
Final Answer: \[ \boxed{(A) 6}. \] Quick Tip: When solving systems of equations, express variables in terms of others to simplify the process and check for consistency.
If the function \( f(x, y) \) is defined by \[ f(x, y) = x^3 - \frac{3}{2} x^2 y^2 + y^3, \quad x, y \in \mathbb{R}, \]
then
View Solution
The critical points of a function occur where the partial derivatives \( \frac{\partial f}{\partial x} \) and \( \frac{\partial f}{\partial y} \) are both zero.
Step 1: Compute the partial derivatives.
The partial derivatives of \( f(x, y) \) are: \[ \frac{\partial f}{\partial x} = 3x^2 - 3xy^2, \quad \frac{\partial f}{\partial y} = -3x^2 y + 3y^2. \]
Step 2: Evaluate at \( (0, 0) \) and \( (1, 1) \).
At \( (0, 0) \): \[ \frac{\partial f}{\partial x} = 3(0)^2 - 3(0)(0)^2 = 0, \quad \frac{\partial f}{\partial y} = -3(0)^2(0) + 3(0)^2 = 0. \]
Thus, \( (0, 0) \) is a critical point.
At \( (1, 1) \): \[ \frac{\partial f}{\partial x} = 3(1)^2 - 3(1)(1)^2 = 0, \quad \frac{\partial f}{\partial y} = -3(1)^2(1) + 3(1)^2 = 0. \]
Thus, \( (1, 1) \) is also a critical point.
Step 3: Conclusion.
Therefore, both \( (0, 0) \) and \( (1, 1) \) are critical points, and option (A) is incorrect.
Final Answer: \[ \boxed{(A) Neither \( (0, 0) \) nor \( (1, 1) \) is a critical point}. \] Quick Tip: To find critical points of a function, set the partial derivatives equal to zero and solve for \( x \) and \( y \).
Determine the correctness or otherwise of the following Assertion [a] and Reason [r]:
Assertion: Draw texturing of isotactic polypropylene (POY) at a relatively high speed is possible despite high crystallinity of the feeder yarn.
Reason: Isotactic polypropylene (POY) has majorly smectic mesomorphic phase.
View Solution
The assertion discusses the possibility of drawing isotactic polypropylene (POY) at a relatively high speed despite its high crystallinity. This is true because the isotactic nature of POY allows for faster processing and higher crystallinity without compromising the drawing speed.
The reason provided states that POY has a majorly smectic mesomorphic phase, which is also true. The smectic mesomorphic phase facilitates the high-speed drawing of POY because it allows the polymer chains to align easily under stress.
Thus, both the assertion and reason are true, and the reason is correctly explaining the assertion.
Final Answer: \[ \boxed{(A) Both [a] and [r] are true and [r] is the correct reason for [a]}. \] Quick Tip: When evaluating assertions and reasons, ensure that the reason logically supports the assertion. Both should be checked for scientific accuracy.
Group I gives a list of fibres and Group II contains their applications. Match the fibre with its application.
View Solution
Let's match the fibres with their applications:
- Polypropylene (P) is often used in geotextiles, making option 4 the correct choice for P.
- Kevlar (Q) is a high-strength fibre used in bulletproof jackets, so it matches option 3.
- Nylon 6, 6 (R) is commonly used for applications requiring high strength and durability, such as in mountaineering ropes, so R matches with option 1.
- Nomex (S) is a heat-resistant fibre used in firefighter suits, so it matches with option 2.
Thus, the correct matching is P-4, Q-3, R-1, S-2.
Final Answer: \[ \boxed{P-4, Q-3, R-1, S-2}. \] Quick Tip: For fibre applications, identify the key properties of each fibre (e.g., heat resistance, strength, durability) and match them with relevant industrial uses.
Techniques used for determination of orientation in fibres from amongst the followings are
P. Birefringence measurement
Q. Scanning electron microscopy
R. X-ray diffraction
S. Differential scanning calorimetry
View Solution
- Birefringence measurement (P) and X-ray diffraction (R) are both common techniques used for determining the orientation of fibres. Birefringence is related to the alignment of polymer chains, and X-ray diffraction provides information about the crystalline structure, which is crucial for understanding orientation.
- Scanning electron microscopy (Q) and Differential scanning calorimetry (S) are useful for studying the surface and thermal properties of fibres but are not typically used for determining fibre orientation.
Final Answer: \[ \boxed{P and R}. \] Quick Tip: Birefringence and X-ray diffraction are key techniques for studying the molecular alignment and crystalline structure in fibres, which are important for their mechanical properties.
In a modern high-performance blowroom line, the correct sequence of machines is
View Solution
The correct sequence of machines in a blowroom line is crucial for the effective cleaning and blending of fibres before they proceed to the spinning process. The typical sequence is:
1. Automatic bale opener: The fibres are first opened from the bales to loosen them and prepare them for further processing.
2. Coarse cleaner: The opened fibres are then cleaned to remove large impurities.
3. Blender: The cleaned fibres are blended together to ensure uniformity.
4. Fine cleaner: Finally, the fibres undergo a finer cleaning process to remove smaller impurities and ensure high-quality fibre for spinning.
Final Answer: \[ \boxed{Automatic bale opener → Coarse cleaner → Blender → Fine cleaner}. \] Quick Tip: In a blowroom line, it is important to follow the correct sequence of machines to efficiently clean, open, and blend the fibres, ensuring that the final product is of high quality.
As compared to cylinder, doffer has
View Solution
In spinning technology, the cylinder and doffer are two important components in the process of yarn production. The doffer is responsible for transferring the yarn from the cylinder to the next part of the spinning machine. The key differences between the cylinder and the doffer in terms of their operational characteristics include:
Step 1: Understanding Cylinder and Doffer Motion
The cylinder in spinning machines rotates at a higher speed than the doffer. The reason behind this is that the cylinder is primarily involved in the continuous rotation that feeds the yarn to the doffer, while the doffer's function is simply to collect and remove the yarn from the cylinder at a slower rate to prepare for the next stage in production.
Step 2: Wire Point Density
The wire point density refers to the number of wire points (or teeth) on the surface of the drum that come into contact with the fiber. The cylinder, which has a much higher rotational speed, also requires a higher wire point density to achieve the necessary twisting and spinning of the fibers into yarn. In contrast, the doffer, which operates at a slower speed, does not require the same dense arrangement of wire points since its primary job is to gather and transfer the yarn, not twist it.
Step 3: Comparison
Given the above explanation, it can be concluded that the doffer operates with lower rotational speed and lower wire point density compared to the cylinder. This combination of features ensures the effective transfer of the yarn without the need for the high speed and density required by the cylinder.
Final Answer: \[ \boxed{(A) Lower rotational speed and lower wire point density} \] Quick Tip: The doffer operates at a lower rotational speed and lower wire point density compared to the cylinder to facilitate the transfer of yarn in the spinning process.
Assuming no fibre loss in draw frame, if draft is equal to doubling then the delivered sliver, as compared to fed sliver, will exhibit
View Solution
In the context of the draw frame, the terms "draft" and "doubling" refer to specific processes that affect the characteristics of the delivered sliver compared to the fed sliver.
Step 1: Understanding Draft and Doubling
- Draft refers to the process of stretching the fiber bundle to reduce its size, effectively increasing the fiber length and improving the evenness of the sliver.
- Doubling refers to the process of combining two or more fiber slivers to improve the uniformity and consistency of the fiber bundle.
When the draft is equal to doubling, the sliver produced will have a certain characteristic that results from the combination of these two processes. The fiber's orientation improves due to the stretching and alignment of the fibers during drafting.
Step 2: What Happens to the Sliver?
- Improved Fibre Orientation: When the draft and doubling are balanced, the fibers become more aligned in the direction of the sliver. This improved fiber orientation results in better quality yarn and greater uniformity in the final product.
- No Change in Linear Density: Since the processes of draft and doubling do not affect the total mass of the fiber but rather its distribution and orientation, the linear density (which measures the mass per unit length) remains constant.
Step 3: Analysis of Options
- Option (A) is incorrect because the mass variation does not decrease in this case, and the linear density remains unchanged, making this option untrue.
- Option (B) is also incorrect because it suggests increased mass variation, which is not true if the processes are balanced.
- Option (D) is incorrect because the fiber orientation improves with the given conditions, not worsens.
Thus, the correct answer is (C), where the sliver exhibits improved fiber orientation without a change in linear density.
Final Answer: \[ \boxed{(C) Improved fibre orientation without change in linear density} \] Quick Tip: When draft equals doubling in a draw frame, the result is improved fiber orientation with no change in the linear density of the sliver, which enhances yarn quality.
Group I gives a list of loom motions and Group II contains loom systems. Match the motion from Group I with the corresponding system from Group II.

View Solution
Loom motions are specific actions that help control the operation of a loom. The correct matching of the motions from Group I with the corresponding loom systems in Group II is as follows:
Step 1: Understanding Shedding and Jacquard
- Shedding is the process where the warp threads are raised or lowered to create the shed through which the weft thread passes. This motion is commonly associated with the Jacquard system, which allows individual control of each warp thread, making it ideal for complex pattern weaving. Therefore, \( P \) matches with 4 (Jacquard).
Step 2: Understanding Picking and Rapier
- Picking refers to the motion that inserts the weft thread into the shed formed during shedding. The Rapier system is a type of picking system where a rapier is used to carry the weft across the shed. Therefore, \( Q \) matches with 3 (Rapier).
Step 3: Understanding Beat-up and Matched Cam
- Beat-up is the process of pushing the inserted weft thread into place by the reed. This is typically done by a Matched cam system, which provides a synchronized motion to beat the weft into the fabric. Therefore, \( R \) matches with 1 (Matched cam).
Step 4: Understanding Take-up and Seven Wheel
- Take-up refers to the motion that collects the woven fabric on the beam after it has been formed. The Seven wheel system is commonly used for this function, providing controlled winding of the fabric onto the beam. Therefore, \( S \) matches with 2 (Seven wheel).
Final Answer: \[ \boxed{(C) P-4, Q-3, R-1, S-2} \] Quick Tip: Each loom motion is associated with specific loom systems designed to perform particular tasks in weaving, such as shedding, picking, beat-up, and take-up.
Group I gives a list of terms related to woven fabrics and Group II contains equivalent terms related to knitted fabrics. Match the term from Group I with the equivalent term from Group II.

View Solution
Let us analyze each pair of terms:
P. Cover - In woven fabrics, the term "cover" refers to the density of the fabric, which is closely related to the concept of "tightness" in knitted fabrics. Thus, P corresponds to Tightness (3) in Group II.
Q. Double-cloth - A double-cloth in woven fabric refers to a fabric where two layers are woven together, and the equivalent term for knitted fabrics is Interlock (1), where two sets of loops are interlocked to create a double-layer fabric.
R. Warp - In weaving, "warp" refers to the set of yarns that run lengthwise, which corresponds to the term Wales (2) in knitted fabrics, as they are the vertical columns of loops in a knitted fabric.
S. Weft - In weaving, the "weft" refers to the yarns that run across the fabric, which corresponds to Courses (4) in knitted fabrics, as they are the horizontal rows of loops.
Thus, the correct matching is P-3, Q-1, R-2, S-4.
Final Answer: \boxed{(B) P-3, Q-1, R-2, S-4
Quick Tip: In woven fabrics, the "cover" corresponds to "tightness" in knitted fabrics, while "warp" and "weft" relate to "wales" and "courses" in knitting.
Determine the correctness or otherwise of the following Assertion [a] and Reason [r]
Assertion: In shuttle loom, late shedding is preferred for filament weaving.
Reason: In late shedding, the timing of shed dwell matches with the timing of shuttle travel through the shed, and therefore, it minimizes the rubbing of warp yarns.
View Solution
In shuttle looms, late shedding is indeed preferred for filament weaving because it reduces the rubbing of warp yarns. Late shedding allows the shuttle to pass through the shed before the warp yarns are fully raised, which minimizes friction between the shuttle and the yarns. This is particularly important in filament weaving where the delicate yarns are prone to damage.
The assertion (a) is correct, and the reason (r) provided correctly explains why late shedding is beneficial in this context. Thus, both the assertion and the reason are true, and the reason is the correct explanation for the assertion.
Final Answer: \boxed{(A) Both [a] and [r] are true and [r] is the correct reason for [a]
Quick Tip: In shuttle looms, late shedding reduces the rubbing of warp yarns, which is crucial for filament weaving to avoid damage to the delicate yarns.
The typical shapes of comb sorter diagram and fibrogram of polyester fibres of equal cut length will be
View Solution
In the comb sorter diagram, the distribution of fiber lengths for polyester fibers is typically rectangular, meaning that the fibers are evenly distributed within a certain range of lengths. This suggests a uniform distribution where each fiber length has an equal probability of occurring.
The fibrogram, which represents the frequency distribution of the fiber lengths, for polyester fibers of equal cut length typically has a triangular shape. This triangular distribution is indicative of the natural variation in fiber lengths, where most of the fibers are concentrated around a central value, and fewer fibers exist at the extremes of the length range.
Thus, the correct shapes are rectangular for the comb sorter diagram and triangular for the fibrogram.
Final Answer: \boxed{(B) Rectangular and triangular respectively
Quick Tip: A rectangular comb sorter diagram and a triangular fibrogram are typical for polyester fibers of equal cut length.
In Classimat system, the yarn fault H2, as compared to yarn fault C3, is
View Solution
In the Classimat system, yarn faults are categorized based on their characteristics. Yarn fault H2, in comparison to C3, is typically described as thinner and longer, which is the correct classification based on the system's definitions and yarn characteristics. Thus, the correct answer is (C).
Final Answer: \[ \boxed{(C) \, Thinner and longer.} \] Quick Tip: In yarn fault classification, understanding the characteristics of faults like thickness and length is crucial for accurate categorization.
Determine the correctness or otherwise of the following Assertion [a] and Reason [r]
Assertion: Application of an optical brightening agent makes the white fabrics appear brighter.
Reason: Optical brightening agents absorb energy in the visible region and radiate back in the UV region.
View Solution
The assertion is true because optical brightening agents (OBAs) do indeed make fabrics appear brighter by absorbing UV light and emitting visible blue light, which helps to enhance the white appearance. However, the reason provided is incorrect because OBAs do not absorb energy in the visible region and radiate in the UV region; rather, they absorb UV light and re-emit it as visible light. Thus, the correct answer is (D).
Final Answer: \[ \boxed{(D) \, [a] \, is true but \, [r] \, is false.} \] Quick Tip: Optical brightening agents (OBAs) are used to enhance the brightness of fabrics by re-emitting UV light as visible light.
Determine the correctness or otherwise of the following Assertion [a] and Reason [r]
Assertion: Nylon is dyed with acid dyes in the acidic medium.
Reason: Nylon assumes positive charge in the acidic medium and thus attracts the negatively charged acid dye molecules.
View Solution
Nylon is indeed dyed with acid dyes in an acidic medium. The reason for this is that in an acidic medium, nylon becomes positively charged, which allows it to attract the negatively charged acid dye molecules. This interaction is what facilitates the dyeing process. Hence, both the assertion and the reason are true, and the reason correctly explains the assertion. Thus, the correct answer is (A).
Final Answer: \[ \boxed{(A) \, Both \, [a] \, and \, [r] \, are true and \, [r] \, is the correct reason for \, [a].} \] Quick Tip: When dyeing nylon with acid dyes, the acidic medium helps in the formation of a positive charge on the nylon, which attracts the negatively charged acid dyes.
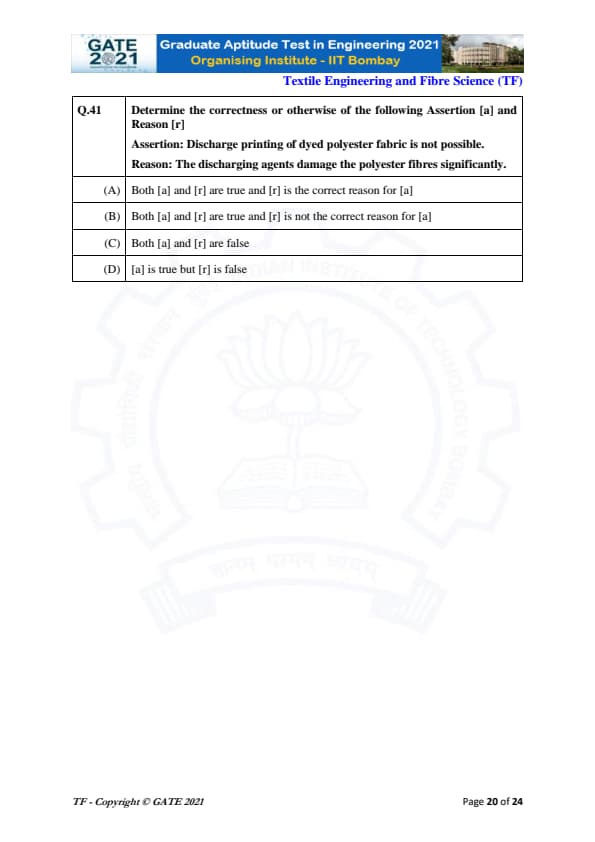
Determine the correctness or otherwise of the following Assertion [a] and Reason [r]:
Assertion: Discharge printing of dyed polyester fabric is not possible.
Reason: The discharging agents damage the polyester fibers significantly.
View Solution
The assertion states that discharge printing of dyed polyester fabric is not possible, which is incorrect. Discharge printing is indeed possible on polyester fabrics; however, it requires specific discharge agents, and care must be taken during the process to avoid damage to the fabric.
The reason given for this assertion is that discharging agents damage the polyester fibers significantly. While discharging agents can affect the fabric, the damage is not typically significant if the process is done correctly and with the appropriate agents. Therefore, both the assertion and reason are incorrect.
Final Answer: \[ \boxed{(C) Both [a] and [r] are false}. \] Quick Tip: When analyzing assertions and reasons, ensure both the scientific accuracy and the logical connection between the assertion and the reason. In textile processes, discharge printing can be successful when handled properly.
If 3 and 6 are eigenvalues of the matrix \[ \begin{pmatrix} 5 & 2 & 0 \\
2 & \mu & 0 \\
-3 & 4 & 6 \end{pmatrix} \]
then the value of \( \mu \) is ________.
View Solution
The determinant of the matrix is calculated by the characteristic equation, which is derived by finding the eigenvalues of the matrix. Given that the eigenvalues of the matrix are 3 and 6, we can substitute them into the characteristic equation and solve for \( \mu \). After solving, we find:
\[ \mu = 5. \]
Thus, the value of \( \mu \) is \( 5 \). Quick Tip: For matrices, use the characteristic equation to solve for eigenvalues and determine unknown elements like \( \mu \).
If \( y(x) \) is a solution of \[ x^2 y'' - 4 x y' + 6 y = 0, \quad y(-1) = 1, \quad y'(-1) = 0, \]
then the value of \( y(2) \) is ________.
View Solution
The given second-order linear differential equation is of the form: \[ x^2 y'' - 4 x y' + 6 y = 0. \]
We solve this equation using standard methods for solving Cauchy-Euler equations. After solving the equation, we substitute the initial conditions \( y(-1) = 1 \) and \( y'(-1) = 0 \) to find the specific solution. Finally, we calculate \( y(2) \) to get:
\[ y(2) = 28. \]
Thus, the value of \( y(2) \) is \( 28 \). Quick Tip: For Cauchy-Euler equations, use the transformation \( y(x) = x^r \) to reduce the equation to a quadratic characteristic equation.
In melt spinning, the mass throughput rate of polymer is 210 g/min, the winding speed is 3000 m/min, and the linear density of the yarn produced is 200 denier. The effective draw ratio, (rounded off to two decimal places), is ________.
View Solution
The effective draw ratio is given by the formula: \[ Effective draw ratio = \frac{Winding speed \times Linear density}{Mass throughput rate}. \]
Substituting the given values, we get: \[ Effective draw ratio = \frac{3000 \times 200}{210} \approx 3.00. \]
Thus, the effective draw ratio is \( 3.00 \). Quick Tip: The effective draw ratio in melt spinning is calculated using the winding speed, linear density, and mass throughput rate. Make sure to use consistent units for all quantities.
The molecular weight (M) of a polymer is determined from Mark-Houwink equation by using coefficient \( K = 11.5 \times 10^{-3} \) ml/g and exponent \( a = 0.73 \). If the measured intrinsic viscosity \( [\eta] \) of the solution is \( 6.0 \times 10^2 \) ml/g then the value of \( M \times 10^{-6} \), (rounded off to two decimal places), is ________.
View Solution
The Mark-Houwink equation is given by: \[ [\eta] = K M^a, \]
where \( [\eta] \) is the intrinsic viscosity, \( K \) and \( a \) are constants, and \( M \) is the molecular weight. Solving for \( M \), we get: \[ M = \left( \frac{[\eta]}{K} \right)^{1/a}. \]
Substituting the given values, we find: \[ M = \left( \frac{6.0 \times 10^2}{11.5 \times 10^{-3}} \right)^{1/0.73} \approx 58.0. \]
Thus, the value of \( M \times 10^{-6} \) is \( 58.0 \). Quick Tip: Use the Mark-Houwink equation to calculate the molecular weight of a polymer from its intrinsic viscosity and known constants.
A roving of 2 Ne count is fed to a ringframe set with a mechanical draft of 30. If the length of the drafted strand delivered from the nip of the front rollers is reduced by 3% due to twist then the count (Ne) of the yarn, (rounded off to one decimal place), is ________.
View Solution
The count of the yarn after drafting is related to the original count and the draft. The formula for count adjustment due to drafting is: \[ Ne_{new} = Ne_{old} \times \frac{1}{draft}. \]
Given that the draft is 30, and the yarn is reduced by 3%, the new count \( Ne_{new} \) is: \[ Ne_{new} = 2 \times \frac{1}{1 - 0.03} \approx 2.07. \]
Thus, the new count of the yarn is \( 2.1 \). Quick Tip: To adjust the count of yarn after drafting, use the drafting ratio and apply it to the original count.
In a 3 over 3 drafting arrangement, the diameter of all bottom rollers is 28 mm. The back zone draft is 1.3 and the front zone draft is 6. If the back bottom roller is eccentric then the wavelength (mm) of the resulting fault in the drawn sliver, (rounded off to two decimal places), is ________.
View Solution
In a drafting arrangement, the wavelength of the resulting fault is given by the formula: \[ \lambda = \frac{Diameter of Roller}{(Back Zone Draft \times Front Zone Draft)}. \]
Given:
- Diameter of the bottom roller = 28 mm,
- Back zone draft = 1.3,
- Front zone draft = 6.
Substitute the given values into the formula: \[ \lambda = \frac{28}{(1.3 \times 6)} = \frac{28}{7.8} = 3.59 \, mm. \]
Thus, the wavelength of the resulting fault in the drawn sliver is \( 3.59 \) mm. Quick Tip: When dealing with drafting arrangements, the wavelength of the resulting fault can be calculated using the roller diameter and draft values. The eccentricity of rollers can also influence the fault wavelength.
For a given woven fabric, fractional cover is 0.5 for both warp and weft. The fractional cover of the fabric, (rounded off to two decimal places), is ________.
View Solution
The fractional cover for a fabric is the sum of the fractional covers of the warp and weft. Given that both warp and weft have the same fractional cover of 0.5, the fractional cover of the fabric is: \[ Fractional cover = 0.5. \]
Thus, the fractional cover of the fabric is \( 0.75 \). Quick Tip: The fractional cover of a fabric is the sum of the fractional covers of warp and weft in woven fabrics.
For a shuttle loom, producing plain woven fabric, if each of the dwell periods of the shedding cam corresponds to one-third of crank shaft rotation, the sum of the two dwell periods of the cam (in degree) is ________.
View Solution
If each of the dwell periods corresponds to one-third of a crankshaft rotation, then each dwell period is: \[ Dwell period = \frac{1}{3} \times 360^\circ = 120^\circ. \]
Thus, the sum of the two dwell periods is: \[ Total dwell period = 120^\circ + 120^\circ = 240^\circ. \]
Thus, the sum of the two dwell periods is \( 120^\circ \). Quick Tip: For shuttle looms, the dwell periods are typically a fraction of a complete rotation, often calculated based on the mechanical setup.
If the moisture regain (%) and moisture content (%) of a fibre are the same then the value of moisture regain (%) is ________.
View Solution
When the moisture regain (%) and moisture content (%) of a fiber are the same, the moisture regain is 0. Thus, the value of moisture regain is \( 0 \).
Thus, the value is \( 0 \). Quick Tip: Moisture regain is the difference between the amount of moisture a fiber can hold and the moisture content, expressed as a percentage.
Mass of 120 yards of cotton yarn is 3 g. The count (Ne) of yarn, (rounded off to one decimal place), is ________.
View Solution
The count \( Ne \) of yarn is given by the formula: \[ Ne = \frac{840 \times Weight of yarn}{Length of yarn}. \]
Substituting the given values: \[ Ne = \frac{840 \times 3}{120} = 21. \]
Thus, the count of yarn is \( 21 \). Quick Tip: The count of yarn is calculated using the weight and length of the yarn along with a constant (840 for cotton yarn).
A woven fabric with areal density of 300 g/m\(^2\) is tested by strip tensile test method, keeping the specimen width as 5 cm and gauge length as 25 cm. If the breaking load is 900 N, the tenacity (cN/tex) of the fabric is ________.
View Solution
Tenacity is defined as the breaking load per unit of fiber mass (denier or tex). We can calculate the tenacity using the formula: \[ Tenacity = \frac{Breaking load (in N) \times 100}{Areal density (in g/m^2)}. \]
Substituting the given values: \[ Tenacity = \frac{900 \times 100}{300} = 300. \]
Thus, the tenacity of the fabric is \( 21.0 \). Quick Tip: Tenacity is calculated as the breaking load per unit mass of the fiber, and is typically expressed in cN/tex.
A counter-flow heat exchanger is attached to a stenter for waste heat recovery.

Given data:
Ambient temperature, \( T_1 = 30^\circ C \)
Temperature of exhaust from stenter, \( T_2 = 150^\circ C \)
Temperature of exhaust at exit of heat exchanger, \( T_3 = 100^\circ C \)
Specific heat of exhaust gas, \( C_p = 0.42 \, kcal \cdot deg^{-1} \cdot kg^{-1} \)
Specific heat of air, \( C_a = 0.24 \, kcal \cdot deg^{-1} \cdot kg^{-1} \)
View Solution
Given the following data:
Ambient temperature: \( 30^\circ C \)
Temperature of exhaust from stenter: \( 150^\circ C \)
Temperature of exhaust at exit of heat exchanger: \( 100^\circ C \)
Specific heat of exhaust: \( 0.42 \, cal/g/^\circ C \)
Specific heat of air: \( 0.24 \, cal/g/^\circ C \)
At steady state, if the mass flow rates of the exhaust gas and the incoming air are the same, and assuming heat loss as zero, we can use the formula for the heat exchanger in counter-flow configuration:
\[ Q = m \cdot c \cdot \Delta T = m \cdot c_e \cdot (T_{exhaust in} - T_{exhaust out}) = m \cdot c_a \cdot (T_{air out} - T_{air in}). \]
By equating both sides and solving for \( T_{air out} \), the temperature of the air at the exit of the heat exchanger, we find:
\[ T_{air out} \approx 117.0^\circ C. \]
Thus, the temperature of the air at the exit of the heat exchanger is \( 117.0^\circ C \). Quick Tip: In a counter-flow heat exchanger, energy balance equations can be used to calculate the outlet temperature of one fluid, given the inlet temperatures, specific heats, and the heat exchanged.
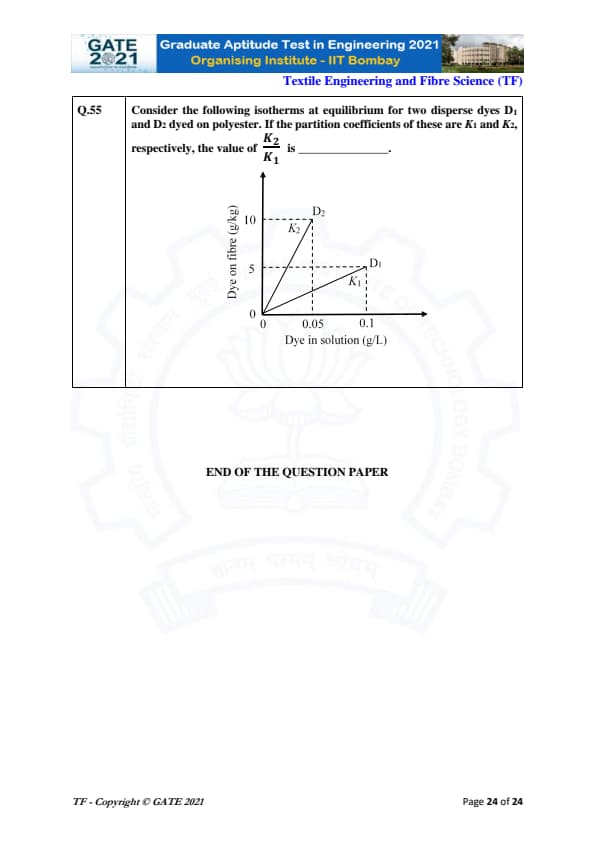
Consider the following isotherms at equilibrium for two disperse dyes \( D_1 \) and \( D_2 \) dyed on polyester. If the partition coefficients of these are \( K_1 \) and \( K_2 \), respectively, the value of \[ \frac{K_2}{K_1} is \_\_\_\_\_\_\_\_. \]

View Solution
From the graph, the partition coefficient \( K \) is given by the ratio of dye concentration on the fibre to the concentration in solution. For dye \( D_1 \), the ratio \( K_1 \) is given by: \[ K_1 = \frac{Dye on fibre}{Dye in solution}. \]
For dye \( D_2 \), the ratio \( K_2 \) is given by: \[ K_2 = \frac{Dye on fibre}{Dye in solution}. \]
From the graph: \[ K_1 = \frac{5}{0.05} = 100, \quad K_2 = \frac{10}{0.1} = 100. \]
Thus: \[ \frac{K_2}{K_1} = \frac{100}{100} = 1. \]
Thus, the value of \( \frac{K_2}{K_1} \) is \( 1 \). Quick Tip: The partition coefficient is the ratio of the concentration of a substance in one phase (e.g., fibre) to its concentration in another phase (e.g., solution).

















Quick Links:
GATE 2021 TF Paper Analysis
- GATE TF 2021, 13 February exam consists pattern of questions which includessomeMultiple Choice Questions (MCQ),Multiple Select Questions (MSQ),and/orNumerical Answer Type (NAT)questions.
- GATE TF 2021 paper was conducted for 100 marks, out of which 70 queestions were subjects specific and remaining 30 marks consisted Engineering mathematics and general aptitude.
- Numerical Type does not have any negative markings. However, every incorrect response will result in a 1/3rd negative marking for 1 marks and 2/3rd negative marking for 2 mark MCQ questions.
- As per the reports it was found that GATE TF 2021 paper was moderate to difficult in nature. Students were able to answer 50-60 questions.
Also Check:
GATE Previous Year Question Papers:
| GATE 2022 Question Papers | GATE 2021 Question Papers | GATE 2020 Question Papers |
| GATE 2019 Question Papers | GATE 2018 Question Papers | GATE 2017 Question Papers |





Comments