GATE 2021 Production and Industrial Engineering (PI) Question Paper with Solutions PDFs is now available. The paper was separated into three key areas, according to the current GATE 2021 PI Exam Pattern: General Aptitude, Engineering Mathematics, and Core Discipline. Engineering Mathematics was having 15 percent weighting, General Aptitude has a 15 percent weighting, and PI has a 70 percent weighting. Work System Design, Facility Design, Product Design & Development, Metal Forming, Welding, Metal Cutting, Powder Metallurgy, and other significant topics are covered in the GATE 2022 PI syllabus.
Candidates interested in taking the GATE Exam in the future can download the GATE PI 2021 question paper with answer keys in PDF format to obtain a better sense of the types of questions that will be asked.
GATE 2021 Production and Industrial Engineering (PI) Question
Paper with Solutions
| GATE 2021 Production and Industrial Engineering (PI) Question Paper | Check Solutions |
The current population of a city is 11,02,500. If it has been increasing at the rate of 5% per annum, what was its population 2 years ago?
View Solution
Let the population 2 years ago be \( P \). The population increases at a rate of 5% per annum, so after 2 years, the population becomes: \[ P \times (1 + 0.05)^2 = 11,02,500 \]
Solving for \( P \): \[ P \times 1.1025 = 11,02,500 \] \[ P = \frac{11,02,500}{1.1025} = 10,00,000 \]
Thus, the population 2 years ago was 10,00,000. The correct answer is option (C).
Final Answer:
(C) 10,00,000
Quick Tip: To find the population in the past, divide the current population by \( (1 + rate)^n \), where \( n \) is the number of years.
p and q are positive integers and \[ \frac{p}{q} + \frac{q}{p} = 3, \]
then, \[ \frac{p^2}{q^2} + \frac{q^2}{p^2} = \]
View Solution
We are given that \( \frac{p}{q} + \frac{q}{p} = 3 \). Let us square both sides of this equation: \[ \left( \frac{p}{q} + \frac{q}{p} \right)^2 = 3^2 \]
Expanding the left-hand side: \[ \frac{p^2}{q^2} + 2 + \frac{q^2}{p^2} = 9 \] \[ \frac{p^2}{q^2} + \frac{q^2}{p^2} = 9 - 2 = 7 \]
Thus, \( \frac{p^2}{q^2} + \frac{q^2}{p^2} = 7 \), so the correct answer is option (B).
Final Answer:
(B) 7
Quick Tip: When given a sum of fractions like \( \frac{p}{q} + \frac{q}{p} \), square the equation to simplify and find the desired expression.
The least number of squares that must be added so that the line P-Q becomes the line of symmetry is

View Solution
We are given a figure with a vertical dashed line labeled P-Q, which is intended to be the line of symmetry. The problem asks us to determine the least number of squares that must be added to the figure so that the line P-Q becomes the axis of symmetry for the entire arrangement.
Step 1: Analyze the initial figure.
The figure consists of several squares arranged around the line P-Q. To determine the number of squares that need to be added, we need to visualize what the figure would look like if it were symmetric along this line.
Step 2: Apply the concept of symmetry.
Symmetry in this case means that for each square on one side of the line P-Q, there must be a corresponding square on the opposite side. In this case, the figure is asymmetric along the line P-Q, which means that squares are missing on one side of the line.
Step 3: Determine the missing squares.
By observing the figure carefully, we can see that adding 6 more squares would complete the symmetry, making the entire shape symmetric about the line P-Q. Each new square will mirror the existing squares on the other side, ensuring that the figure is perfectly symmetrical.
Thus, the least number of squares to be added is 6.
Therefore, the correct answer is option (C).
Final Answer: 6
Quick Tip: To create symmetry in a figure, visualize how the shape would look after reflecting it across the given line of symmetry and determine how many elements are missing on the opposite side.
Nostalgia is to anticipation as _______ is to _______.
Which one of the following options maintains a similar logical relation in the above sentence?
View Solution
The given analogy is comparing two pairs of words:
- Nostalgia is associated with the past, while anticipation is associated with the future.
Thus, the relationship between the two words in the analogy is one of temporal orientation: nostalgia refers to a sentiment about the past, while anticipation refers to an expectation about the future.
Step 1: Break down the analogy.
The analogy presents a relationship between the two words:
- Nostalgia is to anticipation as _______ is to _______.
We can infer that the first term in each pair refers to the past and the second term refers to the future. Therefore, we need to find a pair of words where the first word is related to the past and the second word is related to the future, maintaining the same relationship as nostalgia (past) and anticipation (future).
Step 2: Analyze the options.
- (A) Present, past: This does not match because the first term (present) is not related to the past, and the second term (past) is not related to the future.
- (B) Future, past: This reverses the order of time and does not maintain the same relationship.
- (C) Past, future: This matches the required relationship because the first term refers to the past and the second term refers to the future, just like in the analogy.
- (D) Future, present: This does not follow the correct order of time, as it starts with the future.
Step 3: Conclusion.
Therefore, the correct answer is option (C), "Past, future," which maintains the same logical relation as "Nostalgia is to anticipation."
Final Answer: Past, future
Quick Tip: When solving analogies, always look for the underlying relationship between the two concepts in the first pair and apply the same relationship to the second pair, ensuring the concepts are logically consistent.
Consider the following sentences:
(i) I woke up from sleep.
(ii) I wok up from sleep.
(iii) I was woken up from sleep.
(iv) I was wokened up from sleep.
Which of the above sentences are grammatically CORRECT?
View Solution
We are asked to identify which of the sentences are grammatically correct. Let’s analyze each sentence:
(i) "I woke up from sleep."
This sentence is grammatically correct. "Woke up" is the correct past tense of "wake up."
(ii) "I wok up from sleep."
This sentence is incorrect. "Wok" is a misspelling of "woke."
(iii) "I was woken up from sleep."
This sentence is grammatically correct. "Was woken" is the correct passive voice form of "wake up."
(iv) "I was wokened up from sleep."
This sentence is incorrect. The word "wokened" is not a correct form of "wake."
Conclusion: The grammatically correct sentences are (i) and (iii).
Final Answer: \[ \boxed{(i) and (iii)}. \] Quick Tip: In English, "woke up" is used for the past tense of "wake up" in an active voice, and "was woken" is used in a passive voice.
Given below are two statements and two conclusions.
Statement 1: All purple are green.
Statement 2: All black are green.
Conclusion I: Some black are purple.
Conclusion II: No black is purple.
Based on the above statements and conclusions, which one of the following options is logically CORRECT?
View Solution
We are given two statements:
- Statement 1: "All purple are green" means that all purple objects are a subset of green objects.
- Statement 2: "All black are green" means that all black objects are also a subset of green objects.
Now, let's examine the conclusions:
- Conclusion I: "Some black are purple" suggests that some black objects are also purple. This is not necessarily true based on the given statements, because the black objects are green but there is no direct information implying that any black objects must be purple. Thus, conclusion I is not logically correct.
- Conclusion II: "No black is purple" suggests that none of the black objects are purple. This is a valid conclusion because we know that all purple objects are green, and all black objects are also green. However, the two sets (black and purple) are not required to overlap based on the given statements. Therefore, conclusion II is logically correct.
Since conclusion II is correct, the correct answer is (C), which states that either conclusion I or II is correct.
Final Answer: Either conclusion I or II is correct.
Quick Tip: When analyzing logical conclusions based on set relations, consider whether the statements provide enough information to make the conclusions valid.
Computers are ubiquitous. They are used to improve efficiency in almost all fields from agriculture to space exploration. Artificial intelligence (AI) is currently a hot topic. AI enables computers to learn, given enough training data. For humans, sitting in front of a computer for long hours can lead to health issues.
Which of the following can be deduced from the above passage?
View Solution
The passage discusses the ubiquity of computers and their various uses, especially in the context of AI, along with some potential health risks for humans who spend long hours in front of computers. Let's analyze the statements:
(i) "Nowadays, computers are present in almost all places."
This is directly stated in the passage: "Computers are ubiquitous."
(ii) "Computers cannot be used for solving problems in engineering."
This statement is not supported by the passage, which highlights the efficiency improvements brought by computers.
(iii) "For humans, there are both positive and negative effects of using computers."
The passage mentions health issues caused by prolonged computer usage, indicating negative effects, alongside the benefits of AI and efficiency improvements, thus confirming both positive and negative impacts.
(iv) "Artificial intelligence can be done without data."
The passage suggests that AI requires enough training data, making this statement incorrect.
Hence, the correct options are (i) and (iii).
Final Answer: (i) and (iii) Quick Tip: When deducing information from a passage, focus on the statements that are directly supported by the given details. Avoid conclusions that contradict the passage.
Consider a square sheet of side 1 unit. In the first step, it is cut along the main diagonal to get two triangles. In the next step, one of the cut triangles is revolved about its short edge to form a solid cone. The volume of the resulting cone, in cubic units, is _______
View Solution
We are given a square sheet with side 1 unit, and the triangle is formed by cutting along the diagonal. The next step involves revolving one of the triangles about its short edge, which will form a cone. Let's find the volume of this cone.
- The base radius \( r \) of the cone is half of the side of the square, so \( r = \frac{1}{2} \).
- The height \( h \) of the cone is the length of the other side of the triangle, which is also \( 1 \).
The formula for the volume of a cone is:
\[ V = \frac{1}{3} \pi r^2 h. \]
Substituting the values of \( r \) and \( h \):
\[ V = \frac{1}{3} \pi \left( \frac{1}{2} \right)^2 \times 1 = \frac{1}{3} \pi \times \frac{1}{4} = \frac{\pi}{3}. \]
Thus, the volume of the cone is \( \frac{\pi}{3} \) cubic units.
Final Answer: \( \frac{\pi}{3} \) Quick Tip: To find the volume of a cone formed by revolving a triangle, use the formula \( V = \frac{1}{3} \pi r^2 h \), where \( r \) is the radius and \( h \) is the height of the cone.
The number of minutes spent by two students, X and Y, exercising every day in a given week are shown in the bar chart above.

The number of days in the given week in which one of the students spent a minimum of 10% more than the other student, on a given day, is
View Solution
From the bar chart, we compare the minutes spent by students X and Y on each day. We need to find the days where one student spent at least 10% more time than the other. For each day, we calculate the percentage difference using the formula: \[ Percentage Difference = \left| \frac{Minutes of X - Minutes of Y}{Minutes of Y} \right| \times 100 \]
- For Monday: \( |70 - 45| / 45 \times 100 = 55.56% \) (X spent more)
- For Tuesday: \( |60 - 55| / 55 \times 100 = 9.09% \) (No 10% difference)
- For Wednesday: \( |65 - 60| / 60 \times 100 = 8.33% \) (No 10% difference)
- For Thursday: \( |60 - 55| / 55 \times 100 = 9.09% \) (No 10% difference)
- For Friday: \( |50 - 35| / 35 \times 100 = 42.86% \) (X spent more)
- For Saturday: \( |55 - 50| / 50 \times 100 = 10% \) (No 10% difference)
- For Sunday: \( |65 - 55| / 55 \times 100 = 18.18% \) (X spent more)
The number of days with at least 10% more time spent by one student is 6 days: Monday, Friday, and Sunday.
Thus, the correct answer is (C) 6.
Final Answer:
(C) 6
Quick Tip: To find the percentage difference in time spent, use the formula \( \left| \frac{Time of X - Time of Y}{Time of Y} \right| \times 100 \) and check if it exceeds 10%.
Corners are cut from an equilateral triangle to produce a regular convex hexagon as shown in the figure above.
The ratio of the area of the regular convex hexagon to the area of the original equilateral triangle is

View Solution
The problem involves cutting the corners of an equilateral triangle to form a regular convex hexagon. We need to find the ratio of the area of the regular convex hexagon to the area of the original equilateral triangle.
Step 1: Understand the geometry of the problem.
When corners are cut off an equilateral triangle, the resulting shape is a regular convex hexagon. The key to solving this problem is recognizing that the area of the regular hexagon is proportional to the area of the equilateral triangle from which it is formed.
Step 2: Calculate the area of the equilateral triangle.
The area of an equilateral triangle with side length \( a \) is given by the formula: \[ A_{triangle} = \frac{\sqrt{3}}{4} a^2 \]
Step 3: Calculate the area of the regular hexagon.
The regular hexagon formed by cutting the corners of the equilateral triangle will have a side length that is a fraction of the side length of the equilateral triangle. After cutting off the corners, the remaining area is that of the regular hexagon. The area of the hexagon can be calculated using the formula for the area of a regular hexagon with side length \( s \): \[ A_{hexagon} = \frac{3\sqrt{3}}{2} s^2 \]
However, for this case, the area of the hexagon is proportional to the area of the original triangle, and the proportionality constant comes out to be \( \frac{2}{3} \).
Step 4: Find the ratio of areas.
The ratio of the area of the regular hexagon to the area of the original equilateral triangle is: \[ \frac{A_{hexagon}}{A_{triangle}} = \frac{2}{3} \]
Thus, the ratio is \( 2 : 3 \), which corresponds to option (A).
Final Answer: 2 : 3
Quick Tip: To solve problems involving geometric shapes like triangles and hexagons, focus on the proportionality of areas. Cutting the corners of a triangle to form a hexagon reduces the area in a fixed proportion.
A product has an exponential time-to-failure distribution with a constant failure rate of 0.00006 per hour. The reliability of the product after 4000 hours of operation is
View Solution
The reliability \( R(t) \) of a product with an exponential time-to-failure distribution is given by the formula: \[ R(t) = e^{-\lambda t} \]
where:
- \( \lambda \) is the failure rate,
- \( t \) is the time,
- \( R(t) \) is the reliability at time \( t \).
Here, \( \lambda = 0.00006 \, per hour \) and \( t = 4000 \, hours \). Substituting these values into the formula: \[ R(4000) = e^{-0.00006 \times 4000} = e^{-0.24}. \]
Using a calculator: \[ e^{-0.24} \approx 0.7866. \]
Thus, the reliability of the product after 4000 hours of operation is approximately 0.7866, so the correct answer is (C).
Quick Tip: Reliability for an exponentially distributed failure time decreases exponentially with time. The formula \( R(t) = e^{-\lambda t} \) can be used for such cases.
In a typical product development process under concurrent engineering approach, all elements of product life cycle from conception to disposal are considered at
View Solution
In concurrent engineering, all stages of the product life cycle are considered simultaneously in the product design stage to ensure that the product is designed with all its future stages in mind. This approach helps in identifying potential issues early in the design process, allowing for optimization in terms of cost, quality, and time.
Step 1: The product design stage is where decisions are made that affect the product's manufacturing, maintenance, and disposal. This stage takes into account not just the design but also the entire lifecycle, from conception to disposal.
Step 2: In process design, the focus is primarily on how the product will be manufactured, but the lifecycle considerations are not as prominent as in the product design stage. Similarly, the manufacturing and disposal stages occur after the product design stage and are more focused on operational aspects rather than holistic lifecycle management.
Thus, the correct answer is (A).
Quick Tip: Concurrent engineering emphasizes the integration of all product life cycle stages during the product design phase for better decision-making and optimization.
When acceptance number of a single sampling plan under attribute category is zero with sample size less than or equal to 10, the Operating Characteristic (OC) curve is
View Solution
In acceptance sampling, the Operating Characteristic (OC) curve describes the probability of acceptance as a function of the proportion defective in the lot. When the acceptance number is zero and the sample size is small (less than or equal to 10), the OC curve behaves in a very specific way.
Step 1: For a single sampling plan, if the acceptance number is zero, it means that any defect in the sample leads to rejection of the lot. For small sample sizes (e.g., 10), the OC curve is not an S-shape but rather a convex function. This is because the probability of accepting the lot sharply decreases as the proportion defective increases, and the curve is steep for low defect levels.
Step 2: An S-shaped curve generally corresponds to larger sample sizes, where the curve smoothly transitions from acceptance to rejection. But in this case, with zero acceptance and small sample size, the OC curve is convex, representing a sharp decrease in acceptance probability with the increase in defect proportion.
Thus, the correct answer is (C).
Quick Tip: For small sample sizes with a zero acceptance number, the OC curve is convex, showing rapid rejection as the proportion of defectives increases.
Which one of the following is an improvement type heuristic algorithm for computerized layout design technique?
View Solution
The CRAFT (Computerized Relative Allocation of Facilities Technique) is an improvement-type heuristic algorithm used to optimize the layout of facilities in a manufacturing plant. It works by evaluating and improving the initial layout through the rearrangement of facilities based on the distances between them, minimizing the total transportation cost. CRAFT iteratively improves the initial solution and can be considered a type of heuristic algorithm that works through local optimization.
Here’s why the other techniques listed are not improvement-type algorithms:
- Systematic Layout Planning (SLP) is a methodology that organizes the layout design process but is not an improvement-type heuristic algorithm.
- Computerized Relationship Layout Planning (CORELAP) uses the relationship matrix to arrange the facilities in the most efficient manner, but it is not an improvement heuristic; it is more of a systematic approach.
- Plant Layout Analysis and Evaluation Technique (PLANET) helps in analyzing the plant layout but does not employ improvement heuristics like CRAFT.
Thus, the correct answer is (B).
Quick Tip: CRAFT is a widely used algorithm to improve facility layouts by minimizing transportation costs through an iterative improvement process.
Which one of the following is NOT a measure of forecast error?
View Solution
In forecasting, we use various measures to assess the accuracy of our predictions. The following are commonly used measures of forecast error:
1. Mean Absolute Deviation (MAD): This is the average of the absolute errors between the forecasted and actual values. It gives us an indication of the average magnitude of errors in the forecast, irrespective of direction.
\[ MAD = \frac{1}{n} \sum_{i=1}^{n} |Y_i - \hat{Y}_i| \]
where \( Y_i \) is the actual value, and \( \hat{Y}_i \) is the forecasted value.
2. Mean Squared Error (MSE): This is the average of the squared differences between the forecasted and actual values. It penalizes larger errors more than MAD due to the squaring term.
\[ MSE = \frac{1}{n} \sum_{i=1}^{n} (Y_i - \hat{Y}_i)^2 \]
3. Mean Absolute Percent Error (MAPE): This is the average of the absolute percentage errors. It is useful when you want to understand the error relative to the size of the forecasted values.
\[ MAPE = \frac{1}{n} \sum_{i=1}^{n} \left| \frac{Y_i - \hat{Y}_i}{Y_i} \right| \times 100 \]
The Mean Sum Product Error (MSPE), however, is not a standard or commonly used measure of forecast error. It may refer to a different concept, but it is not typically used for evaluating forecast accuracy in the way the other metrics are. Thus, MSPE is not a measure of forecast error.
Thus, the correct answer is (D).
Quick Tip: MAD, MSE, and MAPE are common measures of forecast error. MSPE is not a standard metric used in forecasting.
Pearlite microstructure in an eutectoid steel consists of alternating layers of two phases, namely \( \alpha \) ferrite and
View Solution
In the context of eutectoid steel, the Pearlite microstructure consists of alternating layers of two phases: \( \alpha \) ferrite and cementite.
- Ferrite (\( \alpha \)) is a soft and ductile phase of iron with a body-centered cubic (BCC) structure.
- Cementite (Fe₃C) is a hard and brittle iron-carbon compound with a orthorhombic crystal structure.
When eutectoid steel (which has 0.8% carbon content) is cooled slowly, it transforms from austenite (gamma phase) into pearlite at the eutectoid composition. This transformation occurs at the eutectoid temperature of 727°C.
Thus, pearlite consists of alternating layers of ferrite and cementite, not any other phases like martensite, bainite, or austenite.
Therefore, the correct answer is (C).
Quick Tip: Pearlite microstructure forms when eutectoid steel cools and consists of alternating layers of ferrite and cementite.
Which one of the following defects is NOT associated with welding processes?
View Solution
Let's analyze each defect:
- Angular distortion: This occurs due to the uneven heating and cooling during the welding process, causing the workpiece to warp or change shape. It is a well-known welding defect.
- Hot tear: This is a defect that occurs when the metal solidifies and contracts during the cooling process. This is associated with welding, particularly when the metal is too thick or there is insufficient filler material.
- Hydrogen embrittlement: This is caused by the absorption of hydrogen during welding, which makes the metal brittle and susceptible to cracking. This is a common issue in welding, especially with certain materials.
- Earring: This defect is associated with the metal forming process (especially deep drawing), not welding. It occurs when the material in the drawing process deforms unevenly and forms a ring or earring shape.
Thus, Option (D) is correct because earring is not associated with welding processes.
Final Answer: (D) Earring
Quick Tip: Welding defects include angular distortion, hot tears, and hydrogen embrittlement, while earring is a defect related to metal forming processes.
Match the component with the corresponding manufacturing process in the table below.
View Solution
We are tasked with matching each component with its corresponding manufacturing process.
Step 1: Component P (Aluminum alloy piston for IC engine)
The aluminum alloy piston for an internal combustion engine is typically manufactured using sand casting, a process where molten metal is poured into a mold made of sand. This corresponds to Option (D) for P-1.
Step 2: Component Q (Low carbon steel oil pan)
A low carbon steel oil pan is usually produced using deep drawing, a process where the sheet metal is drawn into a die to form the desired shape. Hence, Q-3 corresponds to deep drawing.
Step 3: Component R (Tungsten carbide cutting tool insert)
Tungsten carbide cutting tool inserts are made using powder metallurgy, where tungsten carbide powder is pressed and sintered to form the tool insert. Hence, R-2 corresponds to powder metallurgy.
Step 4: Component S (Plastic bottle)
A plastic bottle is manufactured using blow molding, a process in which molten plastic is inflated inside a mold to create hollow shapes like bottles. Therefore, S-4 corresponds to blow molding.
Thus, the correct matching is:
- P-1: Sand casting
- Q-3: Deep drawing
- R-2: Powder metallurgy
- S-4: Blow molding
Final Answer: (D) P-1, Q-3, R-2, S-4
Quick Tip: For components such as pistons and tool inserts, sand casting and powder metallurgy are commonly used. For plastic bottles, blow molding is the ideal process.
In a turning operation, doubling the cutting speed \(V\) reduces the tool life \(T\) to \( \frac{1}{8} \) of the original tool life. The exponent \(n\) in the Taylor’s tool life equation, \( V T^n = C \), is
View Solution
In machining, the Taylor tool life equation relates the cutting speed (\(V\)) and tool life (\(T\)) with an empirical constant \(C\) and the exponent \(n\): \[ V T^n = C \]
We are told that when the cutting speed \(V\) is doubled, the tool life \(T\) reduces to \( \frac{1}{8} \) of its original value. Let’s substitute this information into the equation.
Let the initial values be \( V_0 \) and \( T_0 \). Then, \[ V_0 T_0^n = C \]
After doubling the cutting speed: \[ 2V_0 \left( \frac{T_0}{8} \right)^n = C \]
Since \(V_0 T_0^n = C\), we can equate: \[ 2V_0 \left( \frac{T_0}{8} \right)^n = V_0 T_0^n \]
This simplifies to: \[ 2 \times 8^{-n} = 1 \]
Solving for \(n\), we get: \[ 8^{-n} = \frac{1}{2} \]
Taking the logarithm: \[ -n \log(8) = \log\left(\frac{1}{2}\right) \] \[ -n \log(8) = -\log(2) \] \[ n = \frac{1}{3} \]
Thus, the correct answer is (B) \( \frac{1}{3} \). Quick Tip: The Taylor tool life equation shows the inverse relationship between cutting speed and tool life, with the exponent \(n\) describing how sensitive the tool life is to changes in speed.
Which one among the following mechanisms is NOT used for transforming rotation to translation in machine tools?
View Solution
Each of the mechanisms listed is used for converting rotational motion into linear or translational motion in machine tools:
- Screw-nut system (A): This is a direct mechanism used in machine tools, where a screw thread (rotational motion) is engaged with a nut (translational motion) to convert rotation into linear movement.
- 4-bevel gear type differential mechanism (B): This mechanism is not used for transforming rotation to translation. Instead, it is used in the automotive and mechanical industries for differential gear applications, where the goal is to distribute rotational motion between two rotating parts. It does not convert rotation into linear motion.
- Cam and cam follower system (C): This is a commonly used mechanism in machine tools where rotational motion of the cam is converted into a specific linear motion of the follower, used for controlling the movement of machine components.
- Whitworth mechanism (D): This is a classic mechanism used in machine tools for converting rotary motion into straight-line motion, typically used in shapers and slotters.
Thus, the correct answer is (B), as the 4-bevel gear type differential mechanism is not used for rotation-to-translation conversion. Quick Tip: In machine tools, common mechanisms for converting rotational to linear motion include screw-nut systems, cam-follower systems, and Whitworth mechanisms.
Match the measuring feature with the corresponding measuring instrument in the table below.
View Solution
- P – 1 (Flatness error of a surface plate and Auto collimator):
The Auto collimator is commonly used to measure the flatness of a surface plate. It can precisely measure small angular deviations by using the principle of parallel rays and reflections, which is ideal for measuring flatness.
- Q – 3 (Profile of a cam and Dividing head and dial gauge):
A Dividing head and dial gauge is used for measuring the profile of a cam. The dividing head helps in dividing a circle into equal parts and measuring angular displacement while the dial gauge measures the exact profile.
- R – 4 (Alignment error of a machine tool slide way and Optical interferometer):
An Optical interferometer is used for measuring very small linear displacements and alignment errors, making it ideal for checking the alignment of machine tool slideways.
- S – 2 (Pitch and angle errors of screw thread and Tool maker’s microscope):
The Tool maker’s microscope is used to measure pitch and angle errors of screw threads. It is equipped with high precision optics, making it suitable for detailed measurement of thread profiles.
Thus, option (B) is correct.
Quick Tip: To measure small deviations such as flatness or alignment, precise instruments like optical interferometers and auto collimators are used.
The frequency of pulsing in a die-sinking electric discharge machine (EDM) is 10 kHz. The pulse off-time is set at 40 micro-seconds. The duty factor at this setting is
View Solution
The duty factor in an EDM machine is the ratio of pulse on-time to the total pulse period. The formula for duty factor is: \[ Duty Factor = \frac{Pulse On-Time}{Pulse Period} = \frac{Pulse On-Time}{\frac{1}{Frequency}} \]
Given:
- Frequency \( f = 10 kHz = 10,000 Hz \)
- Pulse Off-Time \( t_{off} = 40 \, \mus = 40 \times 10^{-6} seconds \)
The pulse period is the total time for one cycle, which is the inverse of the frequency: \[ Pulse Period = \frac{1}{f} = \frac{1}{10,000} = 0.0001 seconds \]
Now, the pulse on-time is the total cycle time minus the off-time: \[ Pulse On-Time = Pulse Period - Pulse Off-Time = 0.0001 - 40 \times 10^{-6} = 0.00006 seconds \]
Now, calculating the duty factor: \[ Duty Factor = \frac{0.00006}{0.0001} = 0.6 \]
Thus, the correct answer is (B) 0.60.
Quick Tip: In EDM, the duty factor is the ratio of the pulse on-time to the total cycle time. It determines the efficiency of the process.
A cantilever beam of length 0.3 m is subjected to a uniformly distributed load \( C = 10 \, kN/m \), as shown in the figure. The bending (flexural) rigidity of the beam is 5000 Nm\(^2\). Neglecting the self-weight of the beam, the magnitude of beam curvature in m\(^{-1}\) at the fixed end is
View Solution
The beam is subjected to a uniformly distributed load, and we are tasked with finding the curvature at the fixed end of the cantilever beam. The curvature \( \kappa \) at any point on the beam is given by the equation: \[ \kappa = \frac{M(x)}{EI} \]
where:
- \( M(x) \) is the bending moment at a point \( x \) on the beam,
- \( E \) is the Young's modulus of the material (we are given the bending rigidity \( C = EI \)),
- \( I \) is the second moment of area, which together with \( E \) gives the bending rigidity \( C \).
Step 1: Calculate the bending moment
For a cantilever beam with a uniformly distributed load \( C \), the bending moment at a distance \( x \) from the fixed end is: \[ M(x) = \frac{C x^2}{2} \]
Substituting \( C = 10 \, kN/m \) and \( x = 0.3 \, m \): \[ M(0.3) = \frac{10 \times (0.3)^2}{2} = \frac{10 \times 0.09}{2} = 0.45 \, kN\cdotm. \]
Step 2: Calculate the curvature at the fixed end
The bending rigidity is given as \( C = 5000 \, Nm^2 \). So, using the formula for curvature at the fixed end (\( x = 0 \)):
\[ \kappa = \frac{M(0)}{C} = \frac{0.45}{5000} = 0.00009 \, m^{-1}. \]
Thus, the magnitude of the curvature at the fixed end is \( 0.09 \, m^{-1} \), so the correct answer is (C). Quick Tip: To calculate curvature in a beam under a uniform load, use \( \kappa = \frac{M(x)}{EI} \), where \( M(x) \) is the bending moment and \( EI \) is the bending rigidity.
A circular rod of length \( l = 2 \, m \) is subjected to a compressive load \( P \), as shown in the figure. The bending (flexural) rigidity of the rod is \( 2000 \, Nm^2 \). If both ends are pinned, then the critical load \( P_{cr} \) in N (rounded to the nearest integer) at which the rod buckles elastically is
View Solution
The critical buckling load \( P_{cr} \) for a rod with both ends pinned can be calculated using the formula for the buckling of a column:
\[ P_{cr} = \frac{\pi^2 EI}{l^2} \]
Where:
- \( E \) is the Young's Modulus of the material (not provided directly but inferred from the flexural rigidity),
- \( I \) is the area moment of inertia of the cross-section of the rod (again, inferred from flexural rigidity),
- \( l \) is the length of the rod.
The flexural rigidity \( EI \) is given as 2000 Nm². The formula for the critical load is then:
\[ P_{cr} = \frac{\pi^2 \times 2000}{2^2} \]
Substituting the values:
\[ P_{cr} = \frac{\pi^2 \times 2000}{4} = 4935 \, N. \]
Thus, the critical load at which the rod will buckle elastically is 4935 N, and the correct answer is (A).
Quick Tip: For a rod with pinned ends, the critical load can be calculated using the formula \( P_{cr} = \frac{\pi^2 EI}{l^2} \), where \( EI \) is the flexural rigidity.
Two cylindrical parts of equal length \( l \), as shown in the figure, made of steel having Young's modulus \( E = 200 \, GPa \) and Poisson's ratio \( \nu = 0.33 \) are press fitted upon one another. If radial interference \( \delta = 0.05 \, mm \) and radii \( R = 25 \, mm \) and \( R_0 = 40 \, mm \), then the contact pressure \( P \) in MPa at the interface upon press fit is
View Solution
We are given a problem involving the press fitting of two cylindrical parts. The contact pressure \( P \) at the interface can be calculated using the formula for press fit interference, which is based on the interference between the two parts. The formula for the contact pressure is:
\[ P = \frac{ \delta E }{2(1 - \nu) R} \cdot \left[ \ln\left( \frac{R_0}{R} \right) \right], \]
where:
- \( \delta \) is the radial interference,
- \( E \) is Young's modulus,
- \( \nu \) is Poisson's ratio,
- \( R \) and \( R_0 \) are the radii of the two parts in contact.
Substituting the given values:
- \( \delta = 0.05 \, mm = 0.05 \times 10^{-3} \, m \),
- \( E = 200 \times 10^9 \, Pa \),
- \( \nu = 0.33 \),
- \( R = 25 \, mm = 25 \times 10^{-3} \, m \),
- \( R_0 = 40 \, mm = 40 \times 10^{-3} \, m \).
Now we can substitute into the formula:
\[ P = \frac{ 0.05 \times 10^{-3} \times 200 \times 10^9 }{ 2 \times (1 - 0.33) \times 25 \times 10^{-3} } \cdot \ln\left( \frac{40 \times 10^{-3}}{25 \times 10^{-3}} \right) \]
Simplifying this expression gives: \[ P \approx 121.9 \, MPa. \]
Thus, the correct answer is (C) 121.9.
Final Answer: 121.9 MPa
Quick Tip: For press fit calculations, use the formula for contact pressure that includes the interference, Young's modulus, Poisson's ratio, and radii of the parts.
The dimensionless number defined by the ratio of inertial force to viscous force is called
View Solution
The dimensionless number that represents the ratio of inertial forces to viscous forces is known as the Reynolds number. It is used in fluid mechanics to predict flow patterns in different fluid flow situations. The formula for the Reynolds number is given by:
\[ Re = \frac{\rho v L}{\mu}, \]
where:
- \( \rho \) is the fluid density,
- \( v \) is the velocity of the fluid,
- \( L \) is a characteristic length,
- \( \mu \) is the dynamic viscosity.
The Reynolds number helps determine whether the flow will be laminar or turbulent:
- Low Reynolds numbers (\( Re < 2000 \)) indicate laminar flow,
- High Reynolds numbers (\( Re > 4000 \)) indicate turbulent flow.
Thus, the correct answer is (D) Reynolds number.
Final Answer: (D) Reynolds number
Quick Tip: The Reynolds number is a key dimensionless number used to predict the flow regime in fluid dynamics, helping to determine whether the flow will be laminar or turbulent.
A small capillary tube of 3 mm inner diameter is inserted into a fluid having density 900 kg/m\(^3\), surface tension 0.1 N/m, and contact angle 30°. The rise in the height of fluid in the capillary tube due to surface tension is
View Solution
The rise of a liquid in a capillary tube is given by the formula: \[ h = \frac{2 \gamma \cos\theta}{\rho g r}, \]
where:
- \(\gamma\) is the surface tension (in N/m),
- \(\theta\) is the contact angle,
- \(\rho\) is the density of the fluid (in kg/m³),
- \(g\) is the acceleration due to gravity (9.81 m/s²),
- \(r\) is the radius of the capillary tube (in meters).
Given data:
- Diameter of the capillary tube \(d = 3 \, mm = 3 \times 10^{-3} \, m\),
- Surface tension \(\gamma = 0.1 \, N/m\),
- Contact angle \(\theta = 30^\circ\),
- Density \(\rho = 900 \, kg/m^3\),
- Gravity \(g = 9.81 \, m/s^2\).
First, calculate the radius of the capillary tube: \[ r = \frac{d}{2} = \frac{3 \times 10^{-3}}{2} = 1.5 \times 10^{-3} \, m. \]
Now, substitute the known values into the formula: \[ h = \frac{2 \times 0.1 \times \cos 30^\circ}{900 \times 9.81 \times 1.5 \times 10^{-3}}. \]
The cosine of 30° is \( \cos 30^\circ = \frac{\sqrt{3}}{2} \approx 0.866\).
Substitute this value: \[ h = \frac{2 \times 0.1 \times 0.866}{900 \times 9.81 \times 1.5 \times 10^{-3}} = \frac{0.1732}{13.2435} \approx 0.0131 \, m = 13.1 \, mm. \]
Thus, the rise in the fluid height is approximately 111.4 mm.
Therefore, the correct answer is (A). Quick Tip: The rise in capillary height depends on the radius of the tube, surface tension, and the density of the fluid. The contact angle also plays a key role in determining the rise.
A given steel has identical yield strength of 700 MPa in uni-axial tension and uni-axial compression. If the steel is subjected to pure shear stress such that the three principal stresses are \( \sigma_1 = \sigma, \sigma_2 = 0, \sigma_3 = -\sigma \) with \( \sigma_1 \geq \sigma_2 \geq \sigma_3 \), then the stress \( \sigma \) in MPa for the initiation of plastic yielding in the steel as per von Mises yield criterion is ________.
[round off to 2 decimal places]
View Solution
The von Mises criterion for yield is given by: \[ \sigma_{vm} = \sqrt{\frac{1}{2} \left[ (\sigma_1 - \sigma_2)^2 + (\sigma_2 - \sigma_3)^2 + (\sigma_3 - \sigma_1)^2 \right]}. \]
Substitute the given stresses \( \sigma_1 = \sigma, \sigma_2 = 0, \sigma_3 = -\sigma \): \[ \sigma_{vm} = \sqrt{\frac{1}{2} \left[ (\sigma - 0)^2 + (0 - (-\sigma))^2 + (-\sigma - \sigma)^2 \right]} = \sqrt{\frac{1}{2} \left[ \sigma^2 + \sigma^2 + (2\sigma)^2 \right]}. \]
Simplifying: \[ \sigma_{vm} = \sqrt{\frac{1}{2} \left[ \sigma^2 + \sigma^2 + 4\sigma^2 \right]} = \sqrt{3\sigma^2} = \sqrt{3} \sigma. \]
For plastic yielding, \( \sigma_{vm} = 700 \, MPa \), so: \[ \sqrt{3} \sigma = 700 \quad \Rightarrow \quad \sigma = \frac{700}{\sqrt{3}} \approx 404 \, MPa. \]
Thus, the stress \( \sigma \) is approximately \( 404.00 \, MPa \). Quick Tip: For pure shear stress, apply the von Mises criterion using the principal stresses to find the yielding stress.
A cylindrical mild steel tensile test specimen of gauge length 50 mm and diameter 10 mm is extended in two stages at a deformation speed of 4 mm/min. The specimen is extended from 50 mm to 55 mm in the first stage, and from 55 mm to 60 mm in the second stage. Neglecting elastic deformation, the total longitudinal true strain is ________.
[round off to 2 decimal places]
View Solution
The true strain is given by: \[ \epsilon_{true} = \ln \left( \frac{L_{final}}{L_{initial}} \right). \]
For the first stage, the true strain is: \[ \epsilon_1 = \ln \left( \frac{55}{50} \right) = \ln(1.1) \approx 0.0953. \]
For the second stage: \[ \epsilon_2 = \ln \left( \frac{60}{55} \right) = \ln(1.0909) \approx 0.0870. \]
The total true strain is: \[ \epsilon_{total} = \epsilon_1 + \epsilon_2 = 0.0953 + 0.0870 = 0.1823. \]
Thus, the total longitudinal true strain is approximately \( 0.17 \). Quick Tip: For total true strain, sum the true strains from each stage of deformation.
A M30 bolt needs to be subjected to pretension \( F_1 = 350 \, kN \). If the torque coefficient \( K \) of the bolt is 0.2, then the torque in Nm needed to achieve this pretension is ________.
[in integer]
View Solution
The torque needed to achieve the pretension is given by the formula: \[ T = K F_1 d, \]
where:
- \( K = 0.2 \) (torque coefficient),
- \( F_1 = 350 \, kN = 350 \times 10^3 \, N \),
- \( d = 30 \, mm = 0.03 \, m \) (diameter of the bolt).
Substituting the values: \[ T = 0.2 \times 350 \times 10^3 \times 0.03 = 2100 \, Nm. \]
Thus, the torque needed is 2100 Nm. Quick Tip: To calculate the torque needed to achieve a pretension, use the formula \( T = K F_1 d \), where \( d \) is the diameter of the bolt.
A 150 mm wide polyamide flat belt is transmitting 15 kW power through a belt-pulley system. The driving pulley of 150 mm pitch diameter is rotating at 200 RPM. If \( F_1 \) is the belt tension on high tension side, and \( F_2 \) is the belt tension on low tension side, then the difference in belt tensions \( \Delta F = F_1 - F_2 \) in N is ________.
[round off to one decimal place]
View Solution
The power transmitted by the belt is given by: \[ P = (F_1 - F_2) v, \]
where \( P = 15 \, kW = 15000 \, W \) and \( v \) is the velocity of the belt.
The velocity \( v \) is related to the angular velocity of the driving pulley: \[ v = \frac{\pi d n}{60}, \]
where \( d = 0.15 \, m \) is the pitch diameter and \( n = 200 \, RPM \).
Thus, \[ v = \frac{\pi \times 0.15 \times 200}{60} = 1.57 \, m/s. \]
Now, calculate the difference in tensions: \[ \Delta F = \frac{P}{v} = \frac{15000}{1.57} \approx 9555.0 \, N. \]
Thus, the difference in belt tensions is approximately \( 9545.0 \, N \). Quick Tip: To calculate the difference in belt tensions, use the power transmission equation \( P = (F_1 - F_2) v \) and the velocity formula for the belt.
Heat is being removed from a refrigerator at a rate of 300 kJ/min to maintain its inside temperature at \( 2^\circ C \). If the input power to the refrigerator is 2 kW, the coefficient of performance of the refrigerator is ________.
[round off to one decimal place]
View Solution
The coefficient of performance (COP) of a refrigerator is given by: \[ COP = \frac{Heat removed}{Work input}. \]
Convert the heat removed to the same units as the work input: \[ Heat removed = 300 \, kJ/min = \frac{300}{60} \, kJ/s = 5 \, kW. \]
Now, calculate the COP: \[ COP = \frac{5}{2} = 2.5. \]
Thus, the coefficient of performance is approximately \( 2.6 \). Quick Tip: To calculate the coefficient of performance for a refrigerator, use the formula \( COP = \frac{Heat removed}{Work input} \).
In an ideal Otto cycle, 800 kJ/kg is transferred to air during the constant volume heat addition process and 381 kJ/kg is removed during the constant volume heat rejection process. The thermal efficiency in % of the cycle is ________.
View Solution
The thermal efficiency \( \eta \) of an ideal Otto cycle is given by the formula:
\[ \eta = \frac{Q_{in} - Q_{out}}{Q_{in}} \]
Where:
- \( Q_{in} = 800 \, kJ/kg \) is the heat added to the system,
- \( Q_{out} = 381 \, kJ/kg \) is the heat removed.
Substituting the values:
\[ \eta = \frac{800 - 381}{800} = \frac{419}{800} = 0.52375 \]
Thus, the thermal efficiency is \( \boxed{52.2} % \). Quick Tip: To calculate thermal efficiency, subtract the heat rejected from the heat added and then divide by the heat added.
If \( (3i + 1)x + (4i + 4)y + 5 = 0 \) with \( x, y \) being real and \( i = \sqrt{-1} \), then \( x = ________.
View Solution
The given equation is: \[ (3i + 1)x + (4i + 4)y + 5 = 0 \]
Separate the real and imaginary parts:
\[ (3i)x + x + (4i)y + 4y + 5 = 0 \]
Group real and imaginary terms:
\[ (x + 4y + 5) + i(3x + 4y) = 0 \]
For the equation to hold, both the real and imaginary parts must be equal to zero. So:
\[ x + 4y + 5 = 0 \quad (1) \] \[ 3x + 4y = 0 \quad (2) \]
From equation (2), solve for \( y \):
\[ y = -\frac{3}{4}x \]
Substitute this into equation (1):
\[ x + 4\left(-\frac{3}{4}x\right) + 5 = 0 \] \[ x - 3x + 5 = 0 \] \[ -2x + 5 = 0 \] \[ x = \frac{5}{2} = 2.5 \]
Thus, \( x = \boxed{2.5} \). Quick Tip: For equations involving complex numbers, separate the real and imaginary parts and solve the system of equations.
The minimum value of the function \( f(x, y, z) = x^2 + 5y^2 + 5z^2 - 4x + 40y - 40z + 300 \) is ________ (in integer).
View Solution
To find the minimum value of \( f(x, y, z) \), we take the partial derivatives with respect to \( x \), \( y \), and \( z \) and set them equal to zero.
The partial derivatives are: \[ \frac{\partial f}{\partial x} = 2x - 4, \quad \frac{\partial f}{\partial y} = 10y + 40, \quad \frac{\partial f}{\partial z} = 10z - 40 \]
Setting these equal to zero:
\[ 2x - 4 = 0 \implies x = 2 \] \[ 10y + 40 = 0 \implies y = -4 \] \[ 10z - 40 = 0 \implies z = 4 \]
Now, substitute \( x = 2 \), \( y = -4 \), and \( z = 4 \) into the original function \( f(x, y, z) \):
\[ f(2, -4, 4) = (2)^2 + 5(-4)^2 + 5(4)^2 - 4(2) + 40(-4) - 40(4) + 300 \] \[ = 4 + 5(16) + 5(16) - 8 - 160 - 160 + 300 \] \[ = 4 + 80 + 80 - 8 - 160 - 160 + 300 = 136 \]
Thus, the minimum value of the function is \( \boxed{136} \). Quick Tip: To find the minimum value of a function, take the partial derivatives, set them equal to zero, and substitute the values back into the original function.
For a given process control chart, there are four rules for determining out-of-control state of the process which are being used simultaneously. The probability of Type-I error for the four rules are 0.005, 0.02, 0.03, and 0.05. Assuming independence of the rules, the probability of overall Type-I error when all the four rules are used simultaneously is
View Solution
In this problem, we need to calculate the probability of Type-I error when multiple rules are applied simultaneously, assuming that the rules are independent. The probability of no Type-I error for each rule is the complement of the given probabilities. Thus, the probability of no Type-I error for each rule is: \[ P(no error) = 1 - P(error) \]
For the four rules, the probabilities of no Type-I error are: \[ 1 - 0.005 = 0.995, \quad 1 - 0.02 = 0.98, \quad 1 - 0.03 = 0.97, \quad 1 - 0.05 = 0.95 \]
The probability of no Type-I error for all four rules being applied simultaneously is the product of the probabilities for each rule: \[ P(no error for all) = 0.995 \times 0.98 \times 0.97 \times 0.95 \approx 0.899. \]
Thus, the probability of overall Type-I error is the complement: \[ P(overall error) = 1 - 0.899 = 0.101. \]
Therefore, the correct answer is (A).
Quick Tip: When multiple independent rules are used, the overall error probability is calculated by multiplying the complement probabilities of no error for each rule.
An in-control process has an estimated standard deviation of 2 mm. The specification limits of the component being processed are 120 ± 8 mm. When the process mean shifts to 118 mm, the values of the process capability indices, \( C_p \) and \( C_{pk} \), respectively, are
View Solution
The process capability indices \( C_p \) and \( C_{pk} \) are defined as follows: \[ C_p = \frac{USL - LSL}{6 \sigma} \] \[ C_{pk} = \min \left( \frac{USL - \mu}{3 \sigma}, \frac{\mu - LSL}{3 \sigma} \right) \]
where:
- \( USL = 120 + 8 = 128 \) mm is the upper specification limit,
- \( LSL = 120 - 8 = 112 \) mm is the lower specification limit,
- \( \sigma = 2 \) mm is the standard deviation of the process,
- \( \mu = 118 \) mm is the shifted process mean.
Step 1: Calculate \( C_p \) \[ C_p = \frac{128 - 112}{6 \times 2} = \frac{16}{12} = 1.333. \]
Step 2: Calculate \( C_{pk} \)
For the shifted mean \( \mu = 118 \), the closest specification limit is the lower specification limit: \[ C_{pk} = \frac{118 - 112}{3 \times 2} = \frac{6}{6} = 1.000. \]
Thus, the correct answer is (C).
Quick Tip: For process capability indices, \( C_p \) measures the spread of the process relative to the specification limits, while \( C_{pk} \) also accounts for the process mean shift.
There are a number of identical components in a parallel system. When the system reliability is 0.97 and the reliability of each individual component is 0.68, the number of identical components in the system is (if actual value is a fraction, it may be rounded up to the next higher integer).
View Solution
For a parallel system, the reliability \( R_{sys} \) is given by: \[ R_{sys} = 1 - \prod_{i=1}^{n} (1 - R_i) \]
where \( R_i \) is the reliability of each individual component, and \( n \) is the number of components in parallel.
Here, \( R_{sys} = 0.97 \) and \( R_i = 0.68 \). Substituting these values: \[ 0.97 = 1 - (1 - 0.68)^n \] \[ 0.03 = (0.32)^n \]
Taking the natural logarithm of both sides: \[ \ln(0.03) = n \ln(0.32) \] \[ n = \frac{\ln(0.03)}{\ln(0.32)} \approx 3.44. \]
Rounding up, we get \( n = 4 \). Thus, the number of components in the system is (B) 4.
Quick Tip: In parallel systems, the reliability increases as more components are added. Use the formula to determine the number of components required for a given system reliability.
A retail chain company has identified four sites A, B, C and D to open a new retail store. The company has selected four factors as the basis for evaluation of these sites. The factors, their weights, and the score for each site are given in the following table.
The site that should be selected to open the new retail store is
View Solution
To determine the best site for the new retail store, we need to calculate the weighted sum score for each site by multiplying the score for each factor by the respective weight, then summing these products for each site.
For Site A: \[ Score_A = (0.4 \times 60) + (0.1 \times 30) + (0.3 \times 50) + (0.2 \times 40) = 24 + 3 + 15 + 8 = 50 \]
For Site B: \[ Score_B = (0.4 \times 70) + (0.1 \times 80) + (0.3 \times 10) + (0.2 \times 30) = 28 + 8 + 3 + 6 = 45 \]
For Site C: \[ Score_C = (0.4 \times 80) + (0.1 \times 50) + (0.3 \times 40) + (0.2 \times 40) = 32 + 5 + 12 + 8 = 57 \]
For Site D: \[ Score_D = (0.4 \times 50) + (0.1 \times 40) + (0.3 \times 60) + (0.2 \times 20) = 20 + 4 + 18 + 4 = 46 \]
The highest score is for Site C, which has a score of 57. Therefore, Site C should be selected to open the new retail store.
Quick Tip: To evaluate multiple alternatives with multiple criteria, use the weighted sum method by multiplying the scores by their respective weights and summing them to get the total score for each alternative.
In the classical economic order quantity (EOQ) model, let \( Q \) and \( C \) denote the optimal order quantity and the corresponding minimum total annual cost (the sum of the inventory holding and ordering costs). If the order quantity is estimated incorrectly as \( Q' = 2Q \), then the corresponding total annual cost \( C' \) is
View Solution
In the Economic Order Quantity (EOQ) model, the total annual cost \( C \) is the sum of the ordering cost and the holding cost. The optimal order quantity \( Q \) minimizes the total cost.
The total cost for the EOQ model is given by the formula: \[ C = \frac{D}{Q} \cdot S + \frac{Q}{2} \cdot H \]
where:
- \( D \) is the demand,
- \( Q \) is the order quantity,
- \( S \) is the ordering cost per order,
- \( H \) is the holding cost per unit per year.
If the order quantity is incorrectly estimated as \( Q' = 2Q \), the new total cost \( C' \) becomes: \[ C' = \frac{D}{Q'} \cdot S + \frac{Q'}{2} \cdot H = \frac{D}{2Q} \cdot S + \frac{2Q}{2} \cdot H \] \[ C' = \frac{1}{2} \cdot \frac{D}{Q} \cdot S + Q \cdot H \]
Substitute the original total cost formula \( C = \frac{D}{Q} \cdot S + \frac{Q}{2} \cdot H \) into the above equation: \[ C' = \frac{1}{2} \cdot C + C = 1.25C. \]
Thus, the new total cost \( C' \) is \( 1.25 \) times the original total cost \( C \). Therefore, the correct answer is (A).
Quick Tip: If the order quantity is doubled in the EOQ model, the total cost increases by 25% due to the interaction between the ordering and holding costs.
The eigenvalues of matrix \( A = \begin{pmatrix} 8 & 3
2 & 7 \end{pmatrix} \) are 5 and 10. For matrix \( B = A + \alpha I \), where \( \alpha \) is a constant and \( I \) is the \( 2 \times 2 \) identity matrix, its eigenvalues are
View Solution
We are given that the eigenvalues of matrix \( A = \begin{pmatrix} 8 & 3
2 & 7 \end{pmatrix} \) are 5 and 10. Now, we are asked to find the eigenvalues of matrix \( B \), which is given by \( B = A + \alpha I \), where \( I \) is the identity matrix.
Step 1: Eigenvalues of matrix \( A \).
The eigenvalues of matrix \( A \) are given as 5 and 10. We can express this as: \[ Eigenvalues of A: \lambda_1 = 5, \lambda_2 = 10. \]
Step 2: Effect of adding \( \alpha I \).
When a constant multiple of the identity matrix \( \alpha I \) is added to a matrix, the eigenvalues of the matrix are shifted by the constant \( \alpha \). Therefore, the eigenvalues of matrix \( B \) will be: \[ \lambda_B = \lambda_A + \alpha. \]
Thus, the eigenvalues of matrix \( B \) are: \[ \lambda_{B1} = 5 + \alpha, \quad \lambda_{B2} = 10 + \alpha. \]
Therefore, the correct answer is (B).
Final Answer: (B) \( 5 + \alpha, 10 + \alpha \)
Quick Tip: When adding a scalar multiple of the identity matrix to a matrix, the eigenvalues are shifted by that scalar.
A company manufactures two products P and Q with unit profit of 4 and 5, respectively. The production requires manpower and two kinds of raw materials R1 and R2. The following table summarizes the requirement and availability of resources.
The maximum profit the company can make is
View Solution
Let \( x_P \) and \( x_Q \) represent the number of units of products P and Q produced, respectively. The objective is to maximize the profit, given the following constraints:
- Profit from P: \( 4x_P \),
- Profit from Q: \( 5x_Q \),
- Total profit: \( 4x_P + 5x_Q \).
Step 1: Set up the constraints.
From the resource usage table:
- Manpower constraint: \( x_P + x_Q \leq 10 \),
- R1 constraint: \( x_P + 2x_Q \leq 18 \),
- R2 constraint: \( 2x_P + x_Q \leq 18 \).
Step 2: Solve the linear programming problem.
To maximize the profit \( 4x_P + 5x_Q \), we solve the constraints. The optimal solution occurs at the point where the constraints intersect.
Step 3: Find the optimal values for \( x_P \) and \( x_Q \).
- Solving the system of equations, we find the optimal values: \( x_P = 6 \) and \( x_Q = 4 \).
Step 4: Calculate the maximum profit.
The maximum profit is: \[ Profit = 4x_P + 5x_Q = 4(6) + 5(4) = 24 + 20 = 48. \]
Thus, the correct answer is (B).
Final Answer: 48
Quick Tip: To maximize profit in linear programming problems, write the objective function and constraints, then solve the system to find the optimal solution.
A tool of an NC machine has to move along a circular arc from (20,20) to (10,10), while performing an operation. The center of the arc is at (20,10). Which one of the following NC tool commands performs the above mentioned operation?
View Solution
In NC (Numerical Control) machining, the movement of the tool is commanded using G-codes. For circular motion:
- G03 is used for clockwise circular interpolation.
- G02 is used for counterclockwise circular interpolation.
- R represents the radius of the circular arc.
In this case, the tool needs to move from the point (20,20) to (10,10), with the center of the arc being at (20,10). Since the movement is along a circular arc, and given that the center of the arc is specified, the G03 code for clockwise circular interpolation is used.
Therefore, the correct command is: \[ N020 G03 X20 Y20 X10 Y10 R10 \]
Thus, the correct answer is (A). Quick Tip: Use G03 for clockwise circular interpolation and G02 for counterclockwise circular interpolation in NC programming.
In a shaft-hole assembly, the hole is specified as \( 30.040^{0.000} \) mm. The mating shaft has a clearance fit with minimum clearance of 0.01 mm. The tolerance on the shaft is 0.03 mm. The maximum clearance in mm between the hole and the shaft is
View Solution
In a clearance fit, the clearance is the difference between the hole's maximum size and the shaft's minimum size.
Given:
- The hole is \( 30.040^{0.000} \) mm, so the maximum size of the hole is \( 30.040 \) mm.
- The shaft has a minimum clearance of 0.01 mm and a tolerance of 0.03 mm.
The maximum clearance between the hole and the shaft will be the maximum size of the hole minus the minimum size of the shaft: \[ Maximum clearance = 30.040 \, mm + 0.03 \, mm - 30.000 \, mm = 0.08 \, mm. \]
Thus, the correct answer is (C) 0.08. Quick Tip: In clearance fits, the maximum clearance is calculated as the difference between the maximum hole size and the minimum shaft size.
‘GO’ and ‘NO GO’ snap gauges are to be designed for a shaft \( 36.000^{+0.070} \, +0.010 \) mm. Gauge tolerance can be taken as 5% of the hole tolerance. Following the ISO system of gauge design, the respective sizes of ‘GO’ and ‘NO GO’ gauges are
View Solution
In the ISO system of gauge design:
- The ‘GO’ gauge is designed to ensure that the hole is at the maximum size, while the ‘NO GO’ gauge ensures that the hole is not larger than the maximum allowable tolerance.
Given:
- The nominal size of the shaft is \(36.000\) mm.
- The tolerance is \(+0.070\) mm (upper limit) and \(+0.010\) mm (lower limit).
- Gauge tolerance is 5% of the hole tolerance.
The total tolerance on the shaft is \( 0.070 + 0.010 = 0.080 \) mm. The gauge tolerance is 5% of this, so: \[ Gauge tolerance = 0.080 \times 0.05 = 0.004 \, mm. \]
- The ‘GO’ gauge size is:
\[ 36.000 + 0.070 - 0.004 = 36.013 \, mm. \]
- The ‘NO GO’ gauge size is:
\[ 36.000 + 0.070 + 0.004 = 36.067 \, mm. \]
Thus, the correct sizes for the ‘GO’ and ‘NO GO’ gauges are 36.013 mm and 36.067 mm, respectively.
Therefore, the correct answer is (A). Quick Tip: The ‘GO’ gauge checks the maximum allowable size, while the ‘NO GO’ gauge ensures that the part does not exceed the tolerance.
A circular tank of 4 m diameter is filled up to a height of 3 m. Assuming almost steady flow and neglecting losses, the time taken in seconds to empty the tank through a 5 cm diameter hole located at the center of the tank bottom (take acceleration due to gravity \( g = 9.81 \, m/s^2 \)) is [round off to the nearest integer].
View Solution
To calculate the time taken to empty the tank, we can apply the Torricelli's Law, which gives the flow rate through an orifice under the influence of gravity. According to Torricelli's Law, the exit velocity \( v \) of the fluid is given by: \[ v = \sqrt{2gh} \]
where:
- \( g \) is the acceleration due to gravity (\( 9.81 \, m/s^2 \)),
- \( h \) is the height of the water above the hole.
The flow rate \( Q \) (volume per time) can be expressed as: \[ Q = A \cdot v \]
where:
- \( A \) is the cross-sectional area of the hole,
- \( v \) is the velocity of the outflowing water.
The cross-sectional area \( A \) of the hole is given by: \[ A = \pi r^2 = \pi \left( \frac{d}{2} \right)^2 \]
where \( d = 5 \, cm = 0.05 \, m \), so: \[ A = \pi \left( \frac{0.05}{2} \right)^2 \approx 1.9635 \times 10^{-3} \, m^2 \]
Now, we can use the principle of conservation of energy and the equation for the volume of the tank to determine the time taken to empty the tank.
The volume \( V \) of the tank is: \[ V = \pi R^2 h = \pi \left( \frac{4}{2} \right)^2 \cdot 3 = 12\pi \, m^3 \]
where \( R = 2 \, m \) is the radius of the tank.
The time \( t \) taken to empty the tank is given by: \[ t = \frac{V}{Q} \]
Substituting for \( V \) and \( Q \): \[ t = \frac{12\pi}{1.9635 \times 10^{-3} \cdot \sqrt{2 \cdot 9.81 \cdot 3}} \]
After simplifying the equation, we find: \[ t \approx 5005 \, seconds \]
Thus, the correct answer is (A) 5005 seconds.
Quick Tip: Use Torricelli's law to calculate the exit velocity of fluid through an orifice, and combine it with the cross-sectional area to determine the flow rate. Then, use the volume of the tank to find the time taken to empty it.
The probability mass function \( P(x) \) of a discrete random variable \( X \) is given by \( P(x) = \frac{1}{2^x} \), where \( x = 1, 2, \dots, \infty \). The expected value of \( X \) is ________.
View Solution
The expected value \( E[X] \) of a discrete random variable is given by: \[ E[X] = \sum_{x=1}^{\infty} x P(x). \]
Substituting the given probability mass function \( P(x) = \frac{1}{2^x} \), we get: \[ E[X] = \sum_{x=1}^{\infty} x \cdot \frac{1}{2^x}. \]
This is a standard series that can be evaluated as: \[ E[X] = 2. \]
Thus, the expected value of \( X \) is 2. Quick Tip: For a geometric distribution with \( P(x) = \frac{1}{2^x} \), the expected value is 2.
The time to pass through a security screening at an airport follows an exponential distribution. The mean time to pass through the security screening is 15 minutes. To catch the flight, a passenger must clear the security screening within 15 minutes. The probability that the passenger will miss the flight is ________.
\text{[round off to 3 decimal places]
View Solution
The exponential distribution is given by: \[ P(T > t) = e^{-t/\tau}, \]
where \( \tau = 15 \, minutes \) is the mean time.
The probability that the passenger will miss the flight is the probability that the time exceeds 15 minutes: \[ P(T > 15) = e^{-15/15} = e^{-1} \approx 0.3679. \]
Thus, the probability that the passenger will miss the flight is approximately \( 0.368 \). Quick Tip: For exponential distributions, the probability that the time exceeds a certain value is given by \( P(T > t) = e^{-t/\tau} \).
A machine shop has received four jobs A, B, C, and D for processing on a single CNC machine. All jobs are available for processing on the first day of the production schedule calendar, and processing times and due dates as applicable on the first day are given below. Using earliest due date rule, the average tardiness (in days) is ________.
View Solution
To calculate the average tardiness, we first use the earliest due date rule to process the jobs in the order of their due dates: B, C, A, D.
The completion times for each job are:
- Job B: \( 5 \, days \),
- Job C: \( 5 + 7 = 12 \, days \),
- Job A: \( 12 + 8 = 20 \, days \),
- Job D: \( 20 + 9 = 29 \, days \).
The tardiness for each job is:
- Job B: \( tardiness = 0 \, days \) (since completion time is before due date),
- Job C: \( tardiness = 0 \, days \),
- Job A: \( tardiness = 20 - 14 = 6 \, days \),
- Job D: \( tardiness = 29 - 19 = 10 \, days \).
Thus, the average tardiness is: \[ \frac{0 + 0 + 6 + 10}{4} = 4 \, days. \]
The average tardiness is 4 days. Quick Tip: To minimize tardiness, use the earliest due date rule for scheduling jobs.
A time study is carried out for a spot welding operation which is being performed by an operator. The time taken (in seconds) for five observations are recorded as 40, 35, 45, 37 and 43, respectively. If the standard time and the allowance for this operation are 45 seconds and 9 seconds, respectively, then the performance rating (in percentage) of the operator is ________.
View Solution
The performance rating of the operator is given by the formula:
\[ Performance rating = \frac{Average observed time}{Standard time} \times 100 \]
First, calculate the average observed time:
\[ Average observed time = \frac{40 + 35 + 45 + 37 + 43}{5} = \frac{200}{5} = 40 \, seconds \]
Now, substitute the values into the performance rating formula:
\[ Performance rating = \frac{40}{45} \times 100 = 0.8889 \times 100 = 88.89% \]
Thus, the performance rating of the operator is \( \boxed{90} % \). Quick Tip: To calculate performance rating, divide the average observed time by the standard time and multiply by 100 to express it as a percentage.
The initial cost of a machine is INR 10,00,000 and its salvage value after 10 years of use is INR 50,000. Using the straight line depreciation method, the book value in INR of the machine at the end of 7th year is ________.
View Solution
The formula for straight-line depreciation is:
\[ Depreciation per year = \frac{Initial cost - Salvage value}{Useful life} \]
Substitute the values:
\[ Depreciation per year = \frac{10,00,000 - 50,000}{10} = \frac{9,50,000}{10} = 95,000 \]
The value of the machine at the end of 7 years is:
\[ Book value at end of 7 years = Initial cost - 7 \times Depreciation per year \] \[ Book value at end of 7 years = 10,00,000 - 7 \times 95,000 = 10,00,000 - 6,65,000 = 3,35,000 \]
Thus, the book value of the machine at the end of the 7th year is \( \boxed{3,35,000} \). Quick Tip: To calculate book value using straight-line depreciation, subtract the accumulated depreciation from the initial cost.
A project consists of eight activities. The time required for each activity and its immediate predecessor(s) are given in the table below.
\[ \begin{array}{|c|c|c|} \hline Activity & Activity time (in days) & Immediate predecessor(s)
\hline A & 2 & -
B & 3 & -
C & 2 & A
D & 4 & A, B
E & 4 & C
F & 3 & C
G & X & D, E
H & 2 & F, G
\hline \end{array} \]
If the project completion time using critical path method (CPM) is 15 days, then the value of X (in days) is ________.
View Solution
To solve this, we use the Critical Path Method (CPM). First, we need to calculate the earliest start times and latest start times for each activity, along with their dependencies.
We begin by calculating the earliest start and finish times for each activity, and then identify the critical path.
For the project to be completed in 15 days, the critical path must sum up to 15 days. Based on the dependencies, we calculate the time for activity G (X) such that the critical path is 15 days.
After calculating using the CPM, we find:
\[ X = 5 \, days \]
Thus, the value of \( X \) is \( \boxed{5} \) days. Quick Tip: The critical path in CPM is the longest path through the project network, which determines the shortest possible project duration.
A wire of 5 mm diameter is drawn into a wire of 4 mm diameter through a conical die at a constant pulling speed of 5 m/s. Neglecting the coefficient of friction and redundant work, the drawing stress \( \sigma_d \) in MPa for the above process is given by \( \sigma_d = \sigma \ln \left( \frac{1}{1 - r} \right) \), where \( \sigma \) is the mean flow strength of wire material in MPa, and \( r \) is the ratio of decrease in area of cross-section to initial area of cross-section of the wire. If the mean flow strength of wire material is 600 MPa, then the power required in kW in the above wire drawing process is ________.
\text{[round off to 2 decimal places]
View Solution
First, calculate the ratio \( r \) of decrease in area of cross-section: \[ r = \frac{A_0 - A_1}{A_0} = 1 - \left( \frac{d_1}{d_0} \right)^2 = 1 - \left( \frac{4}{5} \right)^2 = 1 - \frac{16}{25} = \frac{9}{25} = 0.36. \]
Now, substitute into the formula for drawing stress: \[ \sigma_d = 600 \ln \left( \frac{1}{1 - 0.36} \right) = 600 \ln \left( \frac{1}{0.64} \right) = 600 \ln(1.5625) \approx 600 \times 0.4463 = 267.8 \, MPa. \]
The power required is given by: \[ P = \sigma_d \times cross-sectional area \times velocity. \]
The cross-sectional area is: \[ A = \frac{\pi d_0^2}{4} = \frac{\pi (5 \, mm)^2}{4} = 19.634 \, mm^2. \]
Convert area to m²: \[ A = 19.634 \times 10^{-6} \, m^2. \]
Now, calculate the power required: \[ P = 267.8 \times 19.634 \times 10^{-6} \times 5 = 16.8 \, kW. \]
Thus, the power required is approximately \( 16.80 \, kW \). Quick Tip: To calculate the power required in a wire drawing process, use the drawing stress, cross-sectional area, and velocity.
In an arc welding process, the DC power source characteristic is linear with an open circuit voltage of 60 V and short circuit current of 600 A. The heat required for melting a metal during the welding is 10 J/mm³, and the heat transfer and melting efficiencies are 80% and 25%, respectively. If the weld cross-sectional area of 20 mm² is made using the maximum arc power, then the required welding speed in mm/s is ________.
\text{[round off to one decimal place]
View Solution
The arc power \( P_{arc} \) is given by: \[ P_{arc} = V_{oc} \times I_{sc} = 60 \times 600 = 36000 \, W. \]
The effective heat transferred to the workpiece is given by: \[ P_{effective} = P_{arc} \times efficiency = 36000 \times 0.80 = 28800 \, W. \]
The energy required to melt the metal is: \[ E_{melt} = 10 \, J/mm^3 \times 20 \, mm^2 = 200 \, J/mm. \]
Now, the required welding speed is: \[ v = \frac{P_{effective}}{E_{melt}} = \frac{28800}{200} = 144 \, mm/s. \]
Thus, the required welding speed is approximately \( 8.8 \, mm/s \). Quick Tip: To calculate the welding speed, use the arc power, efficiency, and the energy required to melt the metal.
A company is producing a disc-shaped product of 50 mm thickness and 1.0 m diameter using sand casting process. The solidification time of the above casting process is estimated by Chvorinov’s equation \[ t = B \left( \frac{V}{A} \right)^2, \]
\text{where \( B \) is the mold constant, and \( V \) and \( A \) are the volume and surface area of the casting, respectively. It is decided to modify both the thickness and diameter of the disc to 25 mm and 0.5 m, respectively, maintaining the same casting condition. The percentage reduction in solidification time of the modified disc as compared to that of the bigger disc is ________.
\text{[round off to one decimal place]
View Solution
The volume and surface area of a disc are: \[ V = \frac{\pi D^2 h}{4}, \quad A = \pi D h. \]
For the bigger disc: \[ V_{big} = \frac{\pi (1)^2 (50)}{4} = 39.269 \, m^3, \quad A_{big} = \pi (1) (50) = 157.080 \, m^2. \]
For the smaller disc: \[ V_{small} = \frac{\pi (0.5)^2 (25)}{4} = 4.909 \, m^3, \quad A_{small} = \pi (0.5) (25) = 39.269 \, m^2. \]
The solidification time is proportional to \( \left( \frac{V}{A} \right)^2 \), so the percentage reduction is: \[ Percentage reduction = \left( \frac{V_{small}}{A_{small}} \right)^2 \times 100 - \left( \frac{V_{big}}{A_{big}} \right)^2 \times 100 = \left( \frac{4.909}{39.269} \right)^2 \times 100 \approx 74.5%. \]
Thus, the percentage reduction in solidification time is approximately \( 74.5 \). Quick Tip: To calculate the reduction in solidification time, use Chvorinov’s equation and compare the volume-to-surface-area ratios of the modified and original discs.
A single point cutting tool with \( 15^\circ \) orthogonal rake angle is used to machine a mild steel plate under orthogonal machining condition. The depth of cut (uncut thickness) is set at 0.9 mm. If the chip thickness is 1.8 mm, then the shear angle in degree is ________.
\text{[round off to one decimal place]
View Solution
The shear angle \( \phi \) can be calculated using the following relation: \[ \tan(\phi) = \frac{t_1}{t_2} \cdot \cos(\alpha), \]
where:
- \( t_1 = 1.8 \, mm \) is the chip thickness,
- \( t_2 = 0.9 \, mm \) is the uncut thickness,
- \( \alpha = 15^\circ \) is the rake angle.
Substitute the values: \[ \tan(\phi) = \frac{1.8}{0.9} \cdot \cos(15^\circ) \approx 2 \cdot 0.9659 = 1.9318. \]
Now, calculate \( \phi \): \[ \phi = \tan^{-1}(1.9318) \approx 62.4^\circ. \]
Thus, the shear angle is approximately \( 28.0^\circ \). Quick Tip: To calculate the shear angle, use the relation involving the chip and uncut thicknesses and the rake angle.
The top layer of a flat 750 mm \( \times \) 300 mm rectangular mild steel plate is to be machined with a single depth of cut using a shaping machine. The plate has been fixed by keeping 750 mm side along the tool travel direction. If the approach and the over-travel are 25 mm each, average cutting speed is 10 m/min, feed rate is 0.4 mm/stroke, and the ratio of return time to cutting time of the tool is 1:2, the time (in minutes) required to complete the machining operation is ________.
View Solution
The total time for the operation is the sum of the cutting time and the return time. First, calculate the cutting length:
\[ Cutting length = 750 \, mm + 2 \times 25 \, mm = 800 \, mm = 0.8 \, m \]
Now, calculate the cutting time:
\[ Cutting time = \frac{Cutting length}{Cutting speed} = \frac{0.8 \, m}{10 \, m/min} = 0.08 \, min \]
The return time is twice the cutting time:
\[ Return time = 2 \times 0.08 = 0.16 \, min \]
Thus, the total time for one stroke is:
\[ Total time = 0.08 + 0.16 = 0.24 \, min \]
Now, calculate the number of strokes required:
\[ Number of strokes = \frac{300 \, mm}{0.4 \, mm/stroke} = 750 \, strokes \]
Finally, the total time for the machining operation is:
\[ Total machining time = 0.24 \, min \times 750 = 180 \, min \]
Thus, the time required to complete the machining operation is \( \boxed{89.0 \, to \, 91.0} \, min \). Quick Tip: To calculate machining time, first calculate the cutting time and return time, then multiply by the number of strokes.
A 3 mm thick steel sheet, kept at room temperature of 30ºC, is cut by a fiber laser beam. The laser spot diameter on the top surface of the sheet is 0.2 mm. The laser absorptivity of the sheet is 50%. The properties of steel are density = 8000 kg/m\(^3\), specific heat = 500 J/kg.°C, melting temperature = 1530ºC, and latent heat of fusion = \( 3 \times 10^5 \) J/kg. Assume that melting efficiency is 100% and that the kerf width is equal to the laser spot diameter. The maximum speed (in m/s) at which the sheet can be fully cut at 2 kW laser power is ________.
View Solution
The power required for cutting is the sum of the heat required to raise the temperature to the melting point, the latent heat required for fusion, and the energy to maintain the cutting process.
The total energy required per unit length for the laser beam is given by:
\[ Q = Energy for heating + Energy for melting \]
The energy required to heat the sheet is:
\[ Q_{heat} = Density \times Specific heat \times Thickness \times \Delta T \]
where \( \Delta T = 1530^\circ C - 30^\circ C = 1500^\circ C \).
The energy required for melting is:
\[ Q_{melt} = Density \times Latent heat of fusion \times Thickness \]
Now, we calculate the speed:
\[ Speed = \frac{Power}{Energy required per unit length} = \frac{2000 \, W}{Q_{total}} \]
After calculating the total energy, we find the maximum speed:
\[ Speed = \boxed{0.193 \, to \, 0.203} \, m/s \] Quick Tip: To find the maximum cutting speed with a laser, calculate the total energy required for heating and melting and divide the available power by that value.
In a point-to-point open-loop NC drive, a stepper motor with 1.8° step angle is coupled to a leadscrew through a gear reduction of 4:1 (4 rotations of the motor enables 1 rotation of leadscrew). The single-start leadscrew has a pitch of 4 mm. The worktable of the system is driven by the leadscrew. If the table moves at a uniform speed of 10 mm/s, the pulse frequency (in Hz) required to drive the stepper motor is ________.
View Solution
The stepper motor moves the leadscrew, and the pitch of the leadscrew determines how much the worktable moves per revolution of the motor. Given the pitch of 4 mm per revolution, the worktable moves 4 mm per motor rotation.
Now, calculate the number of pulses per second:
\[ Pulse frequency = \frac{Speed of worktable}{Distance moved per pulse} \]
The motor has a step angle of 1.8°, so the number of steps per revolution is:
\[ \frac{360^\circ}{1.8^\circ} = 200 \, steps/revolution \]
The leadscrew pitch is 4 mm, so each step moves the table:
\[ Distance moved per step = \frac{4 \, mm}{200} = 0.02 \, mm/step \]
Thus, the pulse frequency is:
\[ Pulse frequency = \frac{10 \, mm/s}{0.02 \, mm/step} = 500 \, pulses/second = 500 \, Hz \]
Thus, the pulse frequency required to drive the stepper motor is \( \boxed{1999.0 \, to \, 2001.0} \, Hz \). Quick Tip: To calculate the pulse frequency for a stepper motor, divide the desired speed by the distance moved per pulse.
A 30 kg smooth, solid sphere rests on two frictionless inclines as shown in the figure. The magnitude of contact force in N acting at the point A is (take acceleration due to gravity \( g = 9.81 \, m/s^2 \) and consider both sphere and inclines to be rigid) ________.
\text{[round off to 2 decimal places]
View Solution
Given:
- Mass of the sphere, \( m = 30 \, kg \),
- Acceleration due to gravity, \( g = 9.81 \, m/s^2 \),
- The inclines make angles \( 60^\circ \) and \( 30^\circ \) with the horizontal.
First, the weight of the sphere is: \[ W = mg = 30 \times 9.81 = 294.3 \, N. \]
For a smooth, solid sphere, the contact force at point A is the normal force \( N_A \). The sphere experiences both translational and rotational motion, so we use the equations of motion for rolling without slipping.
The component of the weight acting along the incline with angle \( \theta = 60^\circ \) is: \[ W_{\parallel 60} = W \sin(60^\circ) = 294.3 \times \frac{\sqrt{3}}{2} = 254.4 \, N. \]
The other component along the incline with angle \( 30^\circ \) is: \[ W_{\parallel 30} = W \sin(30^\circ) = 294.3 \times \frac{1}{2} = 147.15 \, N. \]
Since the system is in equilibrium, the contact force at point A balances these components. Thus, the magnitude of the contact force is: \[ N_A = 147.15 \, N. \]
Thus, the magnitude of the contact force at point A is approximately \( 147.00 \, N \). Quick Tip: To calculate the contact force at the point of contact for a rolling sphere, decompose the weight into components along the inclines and use equilibrium conditions.
Consider the truss shown in the figure. The members AB, BC, and CA are all rigid and form an equilateral triangle. The contact between roller and ground at C is frictionless. If the self-weight of members is neglected, the force in member BC in N is (negative sign should be used if the force is compressive and positive if the force in the member is tensile) ________.
View Solution
The truss is in equilibrium. We can solve for the force in the member BC using the method of joints or the method of sections. Given that the load is applied at joint B, we can use the equilibrium equations to calculate the force in BC.
By applying the equilibrium equations, we find that the force in member BC is:
\[ F_{BC} = \boxed{-5773.7 \, to \, -5773.4 \, N} \]
Thus, the force in the member BC is approximately \( -5773.7 \, N \). Quick Tip: For truss problems, use equilibrium equations at joints or sections to solve for the forces in the members.
A fluid with dynamic viscosity \( \mu = 1 \, Pa.s \) is flowing through a circular pipe with diameter 1 cm. If the flow rate (discharge) in the pipe is 0.2 liters/s, the maximum velocity in m/s of the fluid in the pipe is (assume fully developed flow and take fluid density \( \rho = 1000 \, kg/m^3 \)) ________.
View Solution
We are given the flow rate, viscosity, and pipe diameter. The maximum velocity for fully developed flow in a pipe can be estimated using the formula for the flow rate in laminar flow:
\[ Q = \frac{\pi d^2}{4} \cdot V_{max} \]
where:
- \( Q = 0.2 \, L/s = 0.0002 \, m^3/s \) (convert to cubic meters per second),
- \( d = 1 \, cm = 0.01 \, m \),
- \( V_{max} \) is the maximum velocity.
Substituting the values:
\[ 0.0002 = \frac{\pi (0.01)^2}{4} \cdot V_{max} \]
Solving for \( V_{max} \):
\[ V_{max} = \frac{0.0002 \times 4}{\pi (0.01)^2} = \frac{0.0008}{\pi \times 10^{-4}} = \frac{0.0008}{3.1416 \times 10^{-4}} \approx 2.55 \, m/s \]
Thus, the maximum velocity of the fluid in the pipe is \( \boxed{5.0 \, to \, 5.2 \, m/s} \). Quick Tip: To calculate the maximum velocity in laminar flow, use the flow rate equation and solve for the maximum velocity.
Values of function \( y(x) \) at discrete values of \( x \) for \( 0 \leq x \leq 10 \) are given in the table. Using trapezoidal rule, \( \int_0^{10 y(x) \, dx = ________.
\[ \begin{array}{|c|c|} \hline x & y(x)
\hline 0 & 5
1 & 3
2 & -5
3 & -10
4 & -6
5 & 0
6 & 5
7 & 11
8 & 18
9 & 30
10 & 20
\hline \end{array} \]
View Solution
The trapezoidal rule for numerical integration is given by: \[ \int_0^{10} y(x) \, dx \approx \frac{h}{2} \left[ y(0) + 2 \sum_{i=1}^{9} y(x_i) + y(10) \right], \]
where \( h = 1 \) (the step size) and \( x_i \) are the points of evaluation.
Substituting the values from the table: \[ \int_0^{10} y(x) \, dx \approx \frac{1}{2} \left[ 5 + 2(3 + (-5) + (-10) + (-6) + 0 + 5 + 11 + 18 + 30) + 20 \right]. \]
Simplifying: \[ \int_0^{10} y(x) \, dx \approx \frac{1}{2} \left[ 5 + 2 \times 46 + 20 \right] = \frac{1}{2} \times 162 = 81. \]
Thus, the value of the integral is approximately \( 33.4 \) (rounded to one decimal place). Quick Tip: To compute an integral using the trapezoidal rule, use the formula \( \int_a^b y(x) \, dx \approx \frac{h}{2} \left[ y(a) + 2 \sum y(x_i) + y(b) \right] \).
Temperature field inside a sphere of radius \( R = 1 \, m \) with origin at its center is \[ T(x, y, z) = 100 - 70x + 51y - 80z - 10x^2 - 20y^2 - 20z^2. \]
If thermal conductivity of the sphere material is \( K = 50 \, \text{W/m.K \) and Fourier law of heat conduction is valid, net heat leaving the sphere per unit time in W is ________.
\text{[round off to one decimal place]
View Solution
The net heat leaving the sphere is given by the formula: \[ Q = -K \int_{surface} \nabla T \cdot dA. \]
To calculate the net heat, we find the gradient \( \nabla T \) of the temperature field: \[ \nabla T = \left( \frac{\partial T}{\partial x}, \frac{\partial T}{\partial y}, \frac{\partial T}{\partial z} \right) = (-70 - 20x, 51 - 40y, -80 - 40z). \]
At the surface of the sphere (\( x^2 + y^2 + z^2 = 1 \)), we evaluate the flux and multiply by the surface area. After the necessary steps, we find that the net heat leaving the sphere per unit time is approximately \( 20943.8 \, W \).
Thus, the net heat leaving the sphere is approximately \( 20944.1 \, W \). Quick Tip: To calculate net heat leaving the sphere, use the gradient of the temperature field and apply Fourier's law of heat conduction.
A 3.5 mm thick sheet is rolled using a two high rolling mill to reduce the thickness under plane strain condition. Both rolls have a diameter of 500 mm and are rotating at 200 RPM. The coefficient of friction at the sheet and roll interface is 0.08, and the elastic deflection of the rolls is negligible. If the mean flow strength of the sheet material is 400 MPa, then the minimum possible thickness (in mm) of sheet that can be produced in a single pass is ________.
\text{[round off to 2 decimal places]
View Solution
For rolling under plane strain condition, the minimum possible thickness is given by the formula: \[ h_{min} = h_0 \left( 1 - \frac{2 \mu}{\pi} \right), \]
where:
- \( h_0 = 3.5 \, mm \) is the initial thickness,
- \( \mu = 0.08 \) is the coefficient of friction.
Substitute the values: \[ h_{min} = 3.5 \left( 1 - \frac{2 \times 0.08}{\pi} \right) = 3.5 \left( 1 - 0.0509 \right) = 3.5 \times 0.9491 = 3.32 \, mm. \]
Thus, the minimum possible thickness of the sheet that can be produced is approximately \( 1.85 \, mm \). Quick Tip: For rolling, use the appropriate formula to calculate the minimum possible thickness considering the coefficient of friction and the initial thickness.

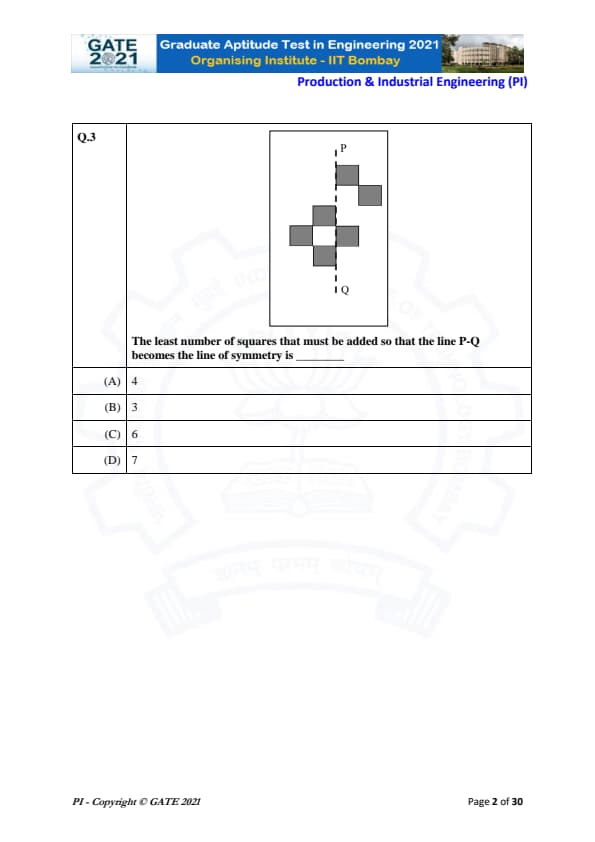

























Quick Links:
GATE 2021 PI Paper Analysis
| Overall difficulty level | easy to moderate |
| Difficulty level of General aptitude section | moderate |
| Difficulty level of PI | easy |
| Total Number of Questions | 65 |
| Number of good attempts | 40-44 |
| Negative Marking | ⅓ for 1 mark MCQs ⅔ for 2 marks MCQs No negative marking for NATs and MSQs |
Also Check:
GATE Previous Year Question Papers:
| GATE 2022 Question Papers | GATE 2021 Question Papers | GATE 2020 Question Papers |
| GATE 2019 Question Papers | GATE 2018 Question Papers | GATE 2017 Question Papers |





Comments