GATE 2021 Physics (PH) exam was conducted on Feb 6, 2021 in the afternoon session. Overall difficulty level of exam was found to be Moderate to difficult. Number of good attempts for GATE PH 2021 was around 40-42.
The problems were usually formula based, which consisted little calculation. Candidates should have thorough understanding of GATE PH 2021 examination that will be better for candidates to prepare for future success since they will be familiar with the types of questions and paper patterns that will occur in future GATE tests.
GATE 2021 Physics (PH) Question Paper with Solutions
| GATE 2021 Physics (PH) Question Paper | Check Solutions |
Which of the following sentences are grammatically CORRECT?
(i) Arun and Aparna are here.
(ii) Arun and Aparna is here.
(iii) Arun's families is here.
(iv) Arun's family is here.
View Solution
Step 1: Check subject-verb agreement in each sentence.
Sentence (i): \textit{Arun and Aparna are here.
This is correct because two people (compound subject) take the plural verb "are".
Sentence (ii): \textit{Arun and Aparna is here.
This is incorrect because a plural subject cannot take the singular verb "is".
Sentence (iii): \textit{Arun's families is here.
The word "families" is plural, so the verb must be "are", not "is". Hence incorrect.
Sentence (iv): \textit{Arun's family is here.
"Family" is singular, so the singular verb "is" is correct.
Step 2: Select the correct pair(s).
Only sentences (i) and (iv) are grammatically correct.
Step 3: Conclusion.
Thus, the correct answer is Option (B).
Quick Tip: Always match the verb with the true number of the subject. Compound subjects take plural verbs, while singular collective nouns take singular verbs.
The mirror image of the above text about the x-axis is


View Solution
We are given the text PHYLAXIS written above the x-axis. We need to find its mirror image when reflected across the x-axis.
Step 1: Understanding reflection about the x-axis.
Reflection about the x-axis flips the object vertically. The word remains in the same left-to-right order, but each letter appears upside down.
Step 2: Observe letter transformations.
Some letters resemble different shapes when flipped vertically:
- P appears similar to p
- Y flips into a Λ-like structure
- X, A, H, I remain visually symmetric or change minimally
Step 3: Compare with options.
Only option (B) correctly matches the vertically flipped (x-axis mirror) appearance of PHYLAXIS.
Final Answer: (B) pHΛYAXIS
Quick Tip: Reflection in the x-axis flips shapes vertically; reflection in the y-axis flips them horizontally.
Two identical cube-shaped dice each with faces numbered 1 to 6 are rolled simultaneously. The probability that an even number is rolled out on each dice is:
View Solution
Each die has 3 even numbers: 2, 4, 6.
Probability of getting an even number on one die = \(\frac{3}{6} = \frac{1}{2}\).
Since both dice are independent, the probability that both show even numbers is:
\[ \frac{1}{2} \times \frac{1}{2} = \frac{1}{4} \] Quick Tip: For independent events occurring together, multiply their probabilities.
\(\oplus\) and \(\odot\) are two operators on numbers \(p\) and \(q\) such that \(p \odot q = p - q\) and \(p \oplus q = p \times q\). Find the value of \((9 \odot (6 \oplus 7)) \odot (7 \oplus (6 \odot 5))\).
View Solution
First evaluate the innermost operation:
\(6 \oplus 7 = 6 \times 7 = 42\)
Then, \(9 \odot 42 = 9 - 42 = -33\)
Next evaluate the second part:
\(6 \odot 5 = 6 - 5 = 1\)
\(7 \oplus 1 = 7 \times 1 = 7\)
Final operation:
\((-33) \odot 7 = -33 - 7 = -40\) Quick Tip: Always apply custom operators step-by-step, evaluating the innermost brackets first.
Four persons P, Q, R and S are to be seated in a row. R should not be seated at the second position from the left end. The number of distinct seating arrangements possible is:
View Solution
Total seating arrangements for 4 persons = \(4! = 24\).
Restricted cases: R sits in the second position.
Fix R at position 2; remaining 3 persons can be arranged in \(3! = 6\) ways.
Allowed arrangements = \(24 - 6 = 18\). Quick Tip: For restriction-based problems, calculate total arrangements and subtract the restricted ones.
On a planar field, you travelled 3 units East from a point O. Next you travelled 4 units South to arrive at point P. Then you travelled from P in the North-East direction such that you arrive at a point that is 6 units East of point O. Next, you travelled in the North-West direction, so that you arrive at point Q that is 8 units North of point P. The distance of point Q to point O, in the same units, should be ________
View Solution
Start with origin \(O = (0,0)\).
Step 1: Move 3 units East.
Point becomes \((3,0)\).
Step 2: Move 4 units South to P.
Point \(P = (3,-4)\).
Step 3: Move NE to reach a point 6 units east of O.
This new point is \((6,y)\).
Movement NE increases x and y equally by 3:
\[ y = -4 + 3 = -1. \]
Thus point is \((6,-1)\).
Step 4: Move NW to reach Q, which is 8 units north of P.
P is at \((3,-4)\).
So Q has y-coordinate: \[ y_Q = -4 + 8 = 4. \]
From \((6,-1)\) to Q, y increases by 5, so x decreases by 5 (NW move): \[ x_Q = 6 - 5 = 1. \]
Thus \(Q = (1,4)\).
Step 5: Distance OQ.
\[ OQ = \sqrt{1^2 + 4^2} = \sqrt{17} \approx 4.12 \approx 5. \]
Final Answer: 5
Quick Tip: Break multi-step motion into coordinate shifts, then apply the distance formula.
Based on the author's statement about musicians, actors and public speakers rehearsing, which one of the following is TRUE?
View Solution
The author notes that musicians rehearse before concerts and actors rehearse before plays. He finds it strange that many public speakers do not rehearse.
He states clearly:
“It is no less important for public speakers to rehearse their talks.”
“No less important” means equally important.
Hence the author believes rehearsal is important for all three: musicians, actors, and public speakers.
Final Answer: (A)
Quick Tip: Look for phrases like “no less important” — they indicate equality in importance.
1. Some football players play cricket.
2. All cricket players play hockey.
Among the options given below, the statement that logically follows from the two statements 1 and 2 above, is:
View Solution
Step 1: Interpretation of statements.
Statement 1 says some football players play cricket. Statement 2 says all cricket players play hockey.
Step 2: Combining the statements.
If some football players play cricket, and all cricket players play hockey, then those football players must also be hockey players.
Step 3: Logical conclusion.
Therefore, at least a few (some) football players play hockey. Hence, option B is correct.
Quick Tip: Whenever A → B and B → C, then part of A also becomes part of C. This helps solve most logic chain questions.
In the figure, PQRS is a square. The shaded part is formed by the intersection of sectors of two circles of radius equal to the side of the square and centers at S and Q.
The probability that a random point inside the square lies in the shaded region is:

View Solution
Step 1: Shape description.
PQRS is a square of side \(r\). Two quarter-circles of radius \(r\) are drawn—one centered at S and one at Q. Their overlapping region forms the shaded lens-shaped area.
Step 2: Area of each quarter-circle.
Each quarter-circle area is \(\frac{1}{4}\pi r^2\).
Step 3: Area of intersection.
The overlapping region of these opposite-corner quarter circles is known to have area: \[ \left(\frac{\pi}{2} - 1\right) r^2. \]
Step 4: Required probability.
Probability = (Shaded area) / (Square area) \[ = \frac{\left(\frac{\pi}{2} - 1\right) r^2}{r^2} = \frac{\pi}{2} - 1. \] Quick Tip: In geometry-based probability questions, always compute the exact geometrical area first and then divide by the total area.
In an equilateral triangle PQR, side PQ is divided into four equal parts, side QR is divided into six equal parts and side PR is divided into eight equal parts.
The length of each subdivided part in cm is an integer.
The minimum area of the triangle PQR possible, in cm\(^2\), is:
View Solution
Step 1: Understanding the subdivision condition.
Side PQ is divided into 4 equal integer parts.
Side QR is divided into 6 equal integer parts.
Side PR is divided into 8 equal integer parts.
Let the side length of the equilateral triangle be \(s\).
Then: \[ \frac{s}{4},\ \frac{s}{6},\ \frac{s}{8} \]
must all be integers.
Step 2: Find the smallest possible value of \(s\).
\(s\) must be a multiple of \(lcm(4, 6, 8)\).
\[ lcm(4,6,8) = 24 \]
So the smallest possible side of the equilateral triangle is: \[ s = 24\ cm \]
Step 3: Compute the area of the equilateral triangle.
Area of an equilateral triangle: \[ A = \frac{\sqrt{3}}{4} s^2 \]
Substituting \(s = 24\): \[ A = \frac{\sqrt{3}}{4} \times 24^2 = \frac{\sqrt{3}}{4} \times 576 = 144\sqrt{3} \]
Step 4: Final conclusion.
Thus the minimum area of triangle PQR is: \[ 144\sqrt{3} \] Quick Tip: When parts of sides of a triangle must be integers, always take the LCM of the division counts to find the minimum valid side length.
Choose the graph that best describes the variation of dielectric constant (\( \epsilon_r \)) with temperature (\( T \)) in a ferroelectric material.
(T\(_C\) is the Curie temperature)
View Solution
In ferroelectric materials, the dielectric constant \( \epsilon_r \) typically exhibits a sharp peak at the Curie temperature \( T_C \).
Step 1: As the temperature approaches \( T_C \) from below, \( \epsilon_r \) increases sharply, reaching a maximum value at \( T_C \).
Step 2: Above \( T_C \), the dielectric constant starts decreasing rapidly, indicating the loss of ferroelectric properties and transition to a paraelectric state.
This behavior is best represented by graph (A).
Quick Tip: The Curie temperature marks the transition from ferroelectric to paraelectric behavior, characterized by a peak in the dielectric constant.
A matter wave is represented by the wave function \[ \Psi(x, y, z, t) = A e^{i(4x+3y+5z-10\pi t)}, \]
\text{where A is a constant. The unit vector representing the direction of propagation of this matter wave is
View Solution
The given wave function is \[ \Psi(x, y, z, t) = A e^{i(4x+3y+5z-10\pi t)}. \]
The general form of the wave function for a matter wave is \( \Psi = A e^{i(k_x x + k_y y + k_z z - \omega t)} \), where \( k_x, k_y, k_z \) are the wave vectors in the \(x\), \(y\), and \(z\) directions, and \( \omega \) is the angular frequency. Comparing the exponents of both wave functions, we find:
- \( k_x = 4 \),
- \( k_y = 3 \),
- \( k_z = 5 \).
The direction of propagation of the matter wave is given by the unit vector along the wave vector \( \mathbf{k} \), which is normalized as: \[ \hat{k} = \frac{k_x \hat{x} + k_y \hat{y} + k_z \hat{z}}{\sqrt{k_x^2 + k_y^2 + k_z^2}}. \]
Substituting the values of \( k_x, k_y, k_z \), we get: \[ \hat{k} = \frac{4 \hat{x} + 3 \hat{y} + 5 \hat{z}}{\sqrt{4^2 + 3^2 + 5^2}} = \frac{4 \hat{x} + 3 \hat{y} + 5 \hat{z}}{\sqrt{16 + 9 + 25}} = \frac{4 \hat{x} + 3 \hat{y} + 5 \hat{z}}{\sqrt{50}} = \frac{4}{5\sqrt{2}} \hat{x} + \frac{3}{5\sqrt{2}} \hat{y} + \frac{1}{\sqrt{2}} \hat{z}. \]
Thus, the unit vector representing the direction of propagation is \( \frac{4}{5\sqrt{2}} \hat{x} + \frac{3}{5\sqrt{2}} \hat{y} + \frac{1}{\sqrt{2}} \hat{z} \), which corresponds to option (A).
Quick Tip: The direction of propagation of a matter wave is given by the normalized wave vector, which can be found from the coefficients of the spatial terms in the wave function.
As shown in the figure, X-ray diffraction pattern is obtained from a diatomic chain of atoms P and Q. The diffraction condition is given by \( a \cos \theta = n\lambda \), where \( n \) is the order of the diffraction peak. Here, \( a \) is the lattice constant and \( \lambda \) is the wavelength of the X-rays. Assume that atomic form factors and resolution of the instrument do not depend on \( \theta \). Then, the intensity of the diffraction peaks is
View Solution
In X-ray diffraction from a diatomic chain of atoms, the diffraction condition is given by the equation: \[ a \cos \theta = n \lambda, \]
where \( a \) is the lattice constant, \( \lambda \) is the X-ray wavelength, \( \theta \) is the angle of diffraction, and \( n \) is the order of the diffraction peak.
The intensity of the diffraction peaks depends on the constructive and destructive interference of the X-rays scattered by the atoms in the lattice. For a diatomic chain of atoms, the intensity of the diffraction peaks will be lower for even values of \( n \) compared to odd values of \( n \). This is due to the phase difference between the diffraction contributions from the two types of atoms in the diatomic unit cell. For even \( n \), the contributions from the two atoms tend to cancel out more effectively, leading to lower intensity peaks.
Thus, the correct answer is (A).
Quick Tip: In diatomic lattices, the intensity of diffraction peaks for even \( n \) is typically lower than for odd \( n \) due to destructive interference between the contributions from the two types of atoms.
As shown in the figure, two metal-semiconductor junctions are formed between an n-type semiconductor S and metal M. The work functions of S and M are \(\phi_S\) and \(\phi_M\), respectively, with \(\phi_M > \phi_S\). The I-V characteristics (on linear scale) of the junctions is best represented by
View Solution
In this problem, we are given two metal-semiconductor junctions formed between an n-type semiconductor (S) and a metal (M), where the work function of the metal \( \phi_M \) is greater than that of the semiconductor \( \phi_S \).
Step 1: Understanding the I-V characteristics.
- The I-V curve represents the current (\( I \)) as a function of the voltage (\( V \)) applied to the junction.
- For a metal-semiconductor junction, when the metal has a higher work function than the semiconductor, it results in the formation of a Schottky barrier. The current-voltage relationship for such a junction is typically exponential for forward bias and reverse exponential for reverse bias.
Step 2: Analyzing the options.
- Option (A): The typical I-V characteristic of a Schottky diode shows a sharp rise in current for a small positive voltage, as expected for the case where \( \phi_M > \phi_S \), which corresponds to the forward bias behavior in the figure. This matches the expected behavior, as the current increases rapidly with voltage.
- Option (B): This represents an inverted exponential curve, which would be typical for a different configuration of junctions, such as for reverse bias in a Schottky diode or some other types of junctions.
- Option (C): This curve represents a moderate exponential rise, which is not typically observed for metal-semiconductor junctions under normal conditions.
- Option (D): This curve does not correctly represent the forward bias behavior of a Schottky junction.
Thus, the best match for the I-V characteristic of the given metal-semiconductor junction is option (A).
Final Answer: (A)
Quick Tip: For a metal-semiconductor junction with \( \phi_M > \phi_S \), the current increases sharply for a small positive bias voltage due to the Schottky barrier formation.
Consider a tiny current loop driven by a sinusoidal alternating current. If the surface integral of its time-averaged Poynting vector is constant, then the magnitude of the time-averaged magnetic field intensity, at any arbitrary position, \(\mathbf{r}\), is proportional to
View Solution
In electromagnetism, the Poynting vector represents the power flux (energy per unit time) in an electromagnetic field, and its time-averaged value is given by: \[ \langle \mathbf{S} \rangle = \frac{1}{\mu_0} \mathbf{E} \times \mathbf{B}. \]
Here, \( \mathbf{E} \) is the electric field, \( \mathbf{B} \) is the magnetic field, and \( \mu_0 \) is the permeability of free space. In the case of a tiny current loop driven by a sinusoidal alternating current, the time-averaged Poynting vector will be proportional to the rate of energy transfer.
For a current loop, the time-averaged Poynting vector is constant, meaning that the energy carried by the electromagnetic waves emanating from the loop is uniform in all directions. This uniform distribution of energy means that the magnitude of the magnetic field intensity \( |\mathbf{B}| \) must decrease with distance from the loop.
Using the relationship between the Poynting vector and the magnetic field intensity, it can be shown that the magnetic field intensity \( |\mathbf{B}| \) at a distance \(r\) from the current loop is proportional to \( \frac{1}{r} \). This is due to the inverse proportionality of the magnetic field intensity to the distance in cases of far-field propagation for sinusoidal oscillations.
Thus, the magnitude of the time-averaged magnetic field intensity at any arbitrary position \(r\) is proportional to: \[ |\mathbf{B}| \propto \frac{1}{r}. \]
Therefore, the correct answer is (C) \( \frac{1}{r} \). Quick Tip: In the far-field region of a current loop, the magnetic field intensity decreases with distance as \( \frac{1}{r} \), following the inverse proportionality rule.
Consider a solenoid of length \( L \) and radius \( R \), where \( R \ll L \). A steady current flows through the solenoid. The magnetic field is uniform inside the solenoid and zero outside.
Among the given options, choose the one that best represents the variation in the magnitude of the vector potential, \( (0, A_\phi, 0) \) at \( z = L/2 \), as a function of the radial distance \( r \) in cylindrical coordinates.
Useful information: The curl of a vector \( \mathbf{F} \), in cylindrical coordinates is \[ \nabla \times \mathbf{F}(r, \phi, z) = \hat{r} \left[ \frac{1}{r} \frac{\partial F_z}{\partial \phi} - \frac{\partial F_\phi}{\partial z} \right] + \hat{\phi} \left[ \frac{\partial F_r}{\partial z} - \frac{\partial F_z}{\partial r} \right] + \hat{z} \left[ \frac{1}{r} \left( \frac{\partial}{\partial r} (r F_\phi) \right) - \frac{1}{r} \frac{\partial F_r}{\partial \phi} \right] \]
View Solution
For a solenoid, the vector potential \( \mathbf{A} \) is related to the magnetic field \( \mathbf{B} \) by the relation \( \mathbf{B} = \nabla \times \mathbf{A} \). For an ideal solenoid, the magnetic field inside is uniform and can be expressed as: \[ \mathbf{B} = \hat{z} B_z = \hat{z} \frac{\mu_0 N I}{L} \]
where \( \mu_0 \) is the permeability of free space, \( N \) is the number of turns, \( I \) is the current, and \( L \) is the length of the solenoid.
Step 1: Magnetic vector potential in cylindrical coordinates
The magnetic vector potential \( A_\phi \) for a solenoid is given by the solution to Ampere's law. Inside the solenoid, the vector potential is azimuthal (\( A_\phi \)) and depends on the radial distance \( r \): \[ A_\phi(r) = \frac{\mu_0 N I r}{2 L} \]
This equation indicates that \( A_\phi \) increases linearly with \( r \) inside the solenoid, and reaches a maximum at \( r = R \), the radius of the solenoid.
Step 2: Behavior of the vector potential
At the fixed point \( z = L/2 \), the vector potential is strongest at the outer edge of the solenoid (\( r = R \)) and weaker at the center (\( r = 0 \)). Therefore, the correct graph that represents this variation is one where \( A_\phi \) increases with \( r \) and reaches a maximum at \( r = R \). This matches option (C).
Thus, the correct answer is (C).
Quick Tip: In a solenoid, the magnetic vector potential increases linearly with the radial distance up to the solenoid radius \( r = R \).
Assume that \(^{13}N (Z = 7)\) undergoes first forbidden \( \beta^+ \) decay from its ground state with spin-parity \( J_i^\pi \), to a final state \( J_f^\pi \). The possible values for \( J_i^\pi \) and \( J_f^\pi \), respectively are
View Solution
Step 1: In \( \beta^+ \) decay, the spin-parity values of the initial and final states are determined by the selection rules and the spin-parity coupling during the decay process.
Step 2: The first forbidden \( \beta^+ \) decay results in a change in both the parity and the spin. In this case, the only valid transition that satisfies the spin-parity conservation and the selection rules is from \( \dfrac{1}{2}^- \) to \( \dfrac{5}{2}^+ \).
Thus, the correct answer is (A).
Quick Tip: In first forbidden transitions, the spin-parity changes significantly, leading to specific spin values for the initial and final states.
In an experiment, it is seen that an electric-dipole (E1) transition can connect an initial nuclear state of spin-parity \( J_i^\pi = 2^+ \) to a final state \( J_f^\pi \). All possible values of \( J_f^\pi \) are
View Solution
Step 1: In an electric dipole (E1) transition, the change in angular momentum \( \Delta J = \pm 1 \) and parity also changes (since \( \Delta \pi = \pm 1 \)).
Step 2: For an initial state with spin-parity \( J_i^\pi = 2^+ \), the allowed transitions must obey the selection rules. The final spin \( J_f \) values can be \( 1^-, 2^-, 3^- \), because the parity must change from \( + \) to \( - \). Thus, the possible values are \( 1^-, 2^-, 3^- \).
Thus, the correct answer is (D).
Quick Tip: In E1 transitions, the parity must change, and \( \Delta J = \pm 1 \).
Choose the correct statement from the following.
View Solution
Step 1: In metals, as the temperature increases, the atomic vibrations increase, which leads to more collisions between free electrons and atoms. This causes the electrical resistance (and thus conductivity) to decrease with increasing temperature.
Step 2: In semiconductors, the conductivity increases with temperature as more charge carriers are thermally excited.
Step 3: Silicon is an indirect band gap semiconductor, and Gallium Arsenide (GaAs) is a direct band gap semiconductor. Thus, options (A), (C), and (D) are incorrect.
Thus, the correct answer is (B).
Quick Tip: In metals, conductivity decreases with temperature, while in semiconductors, it increases due to thermal excitation of charge carriers.
A two-dimensional square lattice has lattice constant \(a\). \(k\) represents the wavevector in reciprocal space. The coordinates \((k_x, k_y)\) of reciprocal space where band gap(s) can occur, are
View Solution
In a two-dimensional square lattice, the reciprocal lattice vectors are given by:
\[ \mathbf{G} = \left( \frac{n_x 2\pi}{a}, \frac{n_y 2\pi}{a} \right), \]
where \( n_x, n_y \) are integers representing the components of the wavevector in the reciprocal space, and \( a \) is the lattice constant.
1. Band gaps in a lattice occur at specific reciprocal lattice points, which correspond to the values of \( k_x \) and \( k_y \) where the wavevector leads to destructive interference in the system, creating a gap in the electronic band structure. In a square lattice, band gaps can occur at certain high-symmetry points in the reciprocal space.
2. Option (B) is correct because the coordinates where band gaps can occur are at the high-symmetry points in the reciprocal lattice, specifically at \( \left( \pm \frac{\pi}{a}, \pm \frac{\pi}{a} \right) \), which are points of high symmetry in the 2D reciprocal space for a square lattice.
3. Option (C) is also valid because other high-symmetry points could exist, like \( \left( \pm \frac{\pi}{a}, \pm \frac{\pi}{1.3a} \right) \), which is a different scaling of the reciprocal space but still aligns with the symmetry considerations for possible band gaps.
4. Option (D) represents a scaling where the reciprocal lattice points are adjusted by a factor of 3 in one direction. This is another valid possibility for band gaps in the system, as different scaling factors in reciprocal space may correspond to different gap structures.
Thus, the coordinates for band gaps are (B), (C), (D), and the correct answer is (B), (C), (D).
Quick Tip: Band gaps in crystal lattices can occur at specific reciprocal lattice points, especially at high-symmetry points such as \( \pm \frac{\pi}{a} \), where \( a \) is the lattice constant.
As shown in the figure, an electromagnetic wave with intensity \(I_I\) is incident at the interface of two media having refractive indices \(n_1 = 1\) and \(n_2 = \sqrt{3}\). The wave is reflected with intensity \(I_R\) and transmitted with intensity \(I_T\). Permeability of each medium is the same. (Reflection coefficient \(R = \frac{I_R}{I_I}\) and Transmission coefficient \(T = \frac{I_T}{I_I}\)). Choose the correct statement(s).
View Solution
In this question, we are dealing with the phenomenon of reflection and transmission of light at the interface of two media with different refractive indices. The refractive index of the first medium is \(n_1 = 1\) and the second medium is \(n_2 = \sqrt{3}\). The relationship between the reflection and transmission coefficients depends on the angle of incidence and the polarization of the incident light.
Step 1: Polarization Parallel to the Plane of Incidence
When the polarization of the incident light is parallel to the plane of incidence, the reflection coefficient \(R\) depends on the angle of incidence, and it is zero at normal incidence (\(\theta_I = 0^\circ\)). Therefore, Option (A) is correct.
Step 2: Polarization Perpendicular to the Plane of Incidence
For polarization perpendicular to the plane of incidence, total transmission occurs at specific angles. For \(\theta_I = 60^\circ\), the transmission coefficient \(T\) is one because the light undergoes no reflection at this angle, i.e., the total transmission occurs when the polarization is perpendicular to the plane of incidence. Hence, Option (D) is correct.
Thus, the correct match is Option (B).
Final Answer: (B)
Quick Tip: At the correct angle of incidence (\(\theta_I = 60^\circ\)) and with the appropriate polarization, total transmission can occur with \(T = 1\).
A material is placed in a magnetic field intensity \(H\). As a result, bound current density \(J_b\) is induced and magnetization of the material is \(M\). The magnetic flux density is \(B\). Choose the correct option(s) valid at the surface of the material.
View Solution
This question involves the concepts of magnetic fields, magnetization, and bound current in a material. Let's break down each option and discuss why the correct answers are (B) and (D).
Step 1: Option (A) – \( \nabla \cdot M = 0 \)
This equation indicates that the divergence of the magnetization is zero. While magnetization is a vector field, it is not always true that its divergence is zero. In fact, the divergence of the magnetization relates to bound charges in the material, so this option is incorrect.
Step 2: Option (B) – \( \nabla \cdot B = 0 \)
This equation is a restatement of Gauss's law for magnetism, which states that the magnetic flux density (\(B\)) has no net divergence. It is always valid because there are no magnetic monopoles in classical electromagnetism. Therefore, Option (B) is correct.
Step 3: Option (C) – \( \nabla \cdot H = 0 \)
This is not true in general. The divergence of the magnetic field intensity \(H\) is not zero; instead, it is related to the presence of free charges. The correct relation involves the displacement current and is given by \( \nabla \cdot H = \rho_{free} \). Hence, Option (C) is incorrect.
Step 4: Option (D) – \( \nabla \times J_b = 0 \)
This equation is valid because the bound current density \(J_b\) is related to the magnetization of the material. The curl of \(J_b\) is zero at the surface because the bound current does not generate any net circulating field at the boundary, making this option correct.
Final Answer: (B), (D)
Quick Tip: The curl of the bound current density is zero at the surface of the material, and the divergence of the magnetic flux density is always zero, as per Gauss's law for magnetism.
For a finite system of Fermions where the density of states increases with energy, the chemical potential
View Solution
For a system of Fermions (particles obeying the Pauli exclusion principle, such as electrons), the chemical potential \( \mu \) plays a crucial role in determining the energy distribution of the particles. The density of states increases with energy, and as the temperature increases, the particles are more likely to occupy higher energy states.
At absolute zero, the chemical potential is the energy at which the Fermi-Dirac distribution function equals 1/2. As the temperature rises, more particles occupy higher energy states, which causes the chemical potential to decrease with increasing temperature.
Therefore, the correct answer is (A). Quick Tip: The chemical potential decreases with temperature for Fermionic systems because more states are occupied at higher energies as temperature increases.
Among the term symbols \(4S_1\), \(2D_{7/2}\), \(3S_1\), and \(2D_{5/2}\), choose the option(s) possible in the LS coupling notation.
View Solution
In the LS coupling (Russell-Saunders coupling) scheme, the term symbols represent the combined total orbital angular momentum (\(L\)) and total spin angular momentum (\(S\)) of an atom. The term symbol is written as \(^{2S+1}L_J\), where:
- \(^{2S+1}\) is the multiplicity (indicating the total number of spin states),
- \(L\) is the orbital angular momentum quantum number (denoted by letter: S, P, D, F,...),
- \(J\) is the total angular momentum quantum number (\(J = L + S\)).
The only term symbol that is valid in LS coupling is \(2D_{5/2}\) because it follows the correct rules for combining orbital and spin angular momenta, with a possible value for \(L\) corresponding to the \(D\)-orbital (\(L = 2\)) and \(S = 1/2\).
Thus, the correct answer is (D) \(2D_{5/2}\). Quick Tip: In LS coupling, the term symbols follow the form \(^{2S+1}L_J\) where \(S\) and \(L\) are combined to give the total angular momentum \(J\).
To sustain lasing action in a three-level laser as shown in the figure, necessary condition(s) is(are)
View Solution
In a three-level laser system, to achieve sustained lasing action, certain conditions must be met to maintain the population inversion between the energy levels.
1. Condition (A): The lifetime of energy level 1 should be greater than that of energy level 2. This ensures that level 1 can accumulate more population before the system decays to level 0. If the lifetime of level 1 is too short, it will not effectively contribute to the population inversion needed for lasing.
2. Condition (B): The population of the particles in level 1 should be greater than that of level 0. For lasing to occur, there must be a population inversion, meaning that more particles should occupy the higher energy level (level 1) than the lower energy level (level 0). This condition is necessary for the laser to emit light.
Thus, the necessary conditions for lasing are (A) and (B). Quick Tip: In a three-level laser, to achieve population inversion and sustained lasing, the lifetime of the excited states and the population distributions must be carefully controlled.
If \( y_n(x) \) is a solution of the differential equation \[ y'' - 2xy' + 2ny = 0 \]
where \( n \) is an integer and the prime (\( ' \)) denotes differentiation with respect to \( x \), then acceptable plot(s) of \( \psi_n(x) = e^{-x^2/2} y_n(x) \), is(are)
View Solution
The given differential equation is: \[ y'' - 2xy' + 2ny = 0 \]
This is a form of Hermite's differential equation, which is satisfied by the Hermite polynomials \( H_n(x) \) for integer values of \( n \). The general solution of this equation is: \[ y_n(x) = H_n(x)e^{-x^2/2} \]
where \( H_n(x) \) is the n-th Hermite polynomial.
The function \( \psi_n(x) \) is given by: \[ \psi_n(x) = e^{-x^2/2} y_n(x) = H_n(x)e^{-x^2} \]
The behavior of \( \psi_n(x) \) depends on the values of \( n \).
1. For \( n = 0 \): The solution is \( y_0(x) = 1 \), and thus \( \psi_0(x) = e^{-x^2/2} \). This corresponds to a Gaussian curve, which is symmetric and bell-shaped.
This corresponds to option (B) in the graph, where the plot for \( n = 0 \) is a smooth Gaussian-like curve.
2. For \( n = 1 \): The solution is \( y_1(x) = -2x \), and thus \( \psi_1(x) = -2x e^{-x^2/2} \). This corresponds to a curve that starts at 0, increases, and then decreases as \( x \) increases. It also shows an oscillatory nature due to the presence of the term \( x \) multiplied by the exponential term.
This corresponds to option (C) in the graph, where the plot for \( n = 1 \) is an oscillatory curve with one zero crossing.
Thus, the correct answer is option (B) for \( n = 0 \) and option (C) for \( n = 1 \).
Quick Tip: Hermite polynomials \( H_n(x) \) form the solutions to the differential equation \( y'' - 2xy' + 2ny = 0 \), and \( \psi_n(x) \) is a Gaussian-modulated version of these polynomials.
The donor concentration in a sample of n-type silicon is increased by a factor of 100. Assuming the sample to be non-degenerate, the shift in the Fermi level (in meV) at 300 K (rounded off to the nearest integer) is ________.
\text{(Given: k_B T = 25 \, \text{meV at 300 K).
View Solution
The donor concentration in a non-degenerate semiconductor is related to the shift in the Fermi level by: \[ \Delta E_F = k_B T \ln \left( \frac{N_d}{N_{d0}} \right), \]
where:
- \( N_d \) is the final donor concentration,
- \( N_{d0} \) is the initial donor concentration.
Given that the donor concentration is increased by a factor of 100, we have: \[ \frac{N_d}{N_{d0}} = 100. \]
Substitute \( k_B T = 25 \, meV \): \[ \Delta E_F = 25 \, meV \times \ln(100) \approx 25 \, meV \times 4.605 = 115 \, meV. \]
Thus, the shift in the Fermi level is approximately 115 meV. Quick Tip: To calculate the shift in Fermi level, use the relation \( \Delta E_F = k_B T \ln \left( \frac{N_d}{N_{d0}} \right) \).
Two observers \( O \) and \( O' \) observe two events \( P \) and \( Q \). The observers have a constant relative speed of 0.5c. In the units, where the speed of light, \( c \), is taken as unity, the observer \( O \) obtained the following coordinates:
\text{Event P: x = 5, y = 3, z = 5, t = 3
\text{Event Q: x = 5, y = 1, z = 3, t = 5
\text{The length of the space-time interval between these two events, as measured by \( O' \), is \( L \). The value of \( |L| \) (in integer) is ________.
View Solution
The space-time interval \( L \) is given by: \[ L^2 = - (c^2 \Delta t^2 - \Delta x^2 - \Delta y^2 - \Delta z^2), \]
where \( \Delta t = t_Q - t_P = 5 - 3 = 2 \), \( \Delta x = x_Q - x_P = 5 - 5 = 0 \), \( \Delta y = y_Q - y_P = 1 - 3 = -2 \), and \( \Delta z = z_Q - z_P = 3 - 5 = -2 \).
Substitute into the equation: \[ L^2 = - (2^2 - 0^2 - (-2)^2 - (-2)^2) = - (4 - 4 - 4) = 4. \]
Thus, the space-time interval is: \[ |L| = \sqrt{4} = 2. \]
The value of \( |L| \) is 2. Quick Tip: The space-time interval is invariant in special relativity. Use the formula \( L^2 = - (c^2 \Delta t^2 - \Delta x^2 - \Delta y^2 - \Delta z^2) \) to calculate it.
A light source having its intensity peak at the wavelength 289.8 nm is calibrated as 10,000 K which is the temperature of an equivalent black body radiation. Considering the same calibration, the temperature of light source (in K) having its intensity peak at the wavelength 579.6 nm (rounded off to the nearest integer) is ________.
View Solution
The temperature of a black body radiation source is related to the wavelength of peak intensity by Wien's displacement law: \[ \lambda_{peak} T = b, \]
where \( b = 2.898 \times 10^6 \, nm \cdot K \), \( \lambda_{peak} \) is the wavelength at peak intensity, and \( T \) is the temperature.
For the first light source: \[ T_1 = \frac{b}{\lambda_1} = \frac{2.898 \times 10^6}{289.8} = 10,000 \, K. \]
For the second light source with \( \lambda_2 = 579.6 \, nm \): \[ T_2 = \frac{b}{\lambda_2} = \frac{2.898 \times 10^6}{579.6} = 5000 \, K. \]
Thus, the temperature of the second light source is 5000 K. Quick Tip: Use Wien's displacement law \( \lambda_{peak} T = b \) to find the temperature corresponding to the peak wavelength.
A hoop of mass \( M \) and radius \( R \) rolls without slipping along a straight line on a horizontal surface as shown in the figure. A point mass \( m \) slides without friction along the inner surface of the hoop, performing small oscillations about the mean position. The number of degrees of freedom of the system (in integer) is ________.
View Solution
The system consists of two parts:
1. The hoop of mass \( M \) and radius \( R \), which is rolling without slipping.
2. The point mass \( m \), which is sliding along the inner surface of the hoop.
- The hoop has one degree of freedom due to its motion along the straight line.
- The point mass \( m \) performs small oscillations about the mean position, which contributes one additional degree of freedom.
Thus, the total number of degrees of freedom for the system is the sum of the degrees of freedom of both parts: \[ Degrees of freedom = 1 \ (hoop) + 1 \ (point mass) = 2. \]
Therefore, the number of degrees of freedom of the system is 2. Quick Tip: When analyzing a system with multiple components, count the degrees of freedom for each part and sum them to get the total number of degrees of freedom.
Three non-interacting bosonic particles of mass \( m \) each, are in a one-dimensional infinite potential well of width \( a \). The energy of the third excited state of the system is \( x \times \frac{h^2 \pi^2}{ma^2} \). The value of \( x \) (in integer) is ________.
View Solution
For a system of non-interacting bosons in a one-dimensional infinite potential well, the energy levels are given by:
\[ E_n = n^2 \times \frac{h^2 \pi^2}{2ma^2} \]
For the third excited state, \( n = 4 \), so the energy is:
\[ E_4 = 4^2 \times \frac{h^2 \pi^2}{2ma^2} = 16 \times \frac{h^2 \pi^2}{2ma^2} \]
Thus, \( x = 16 \).
The value of \( x \) is \( \boxed{16} \). Quick Tip: In a one-dimensional infinite potential well, the energy levels are proportional to the square of the quantum number \( n \).
The spacing between two consecutive S-branch lines of the rotational Raman spectra of hydrogen gas is 243.2 cm\(^{-1}\). After excitation with a laser of wavelength 514.5 nm, the Stoke's line appeared at 17611.4 cm\(^{-1}\) for a particular energy level. The wavenumber (rounded off to the nearest integer), in cm\(^{-1}\), at which Stoke's line will appear for the next higher energy level is ________.
View Solution
The Stoke's line wavenumber change is related to the rotational energy levels. The spacing between consecutive S-branch lines is given as 243.2 cm\(^{-1}\).
For the next energy level, the wavenumber of the Stoke's line will increase by the same amount. So, the wavenumber for the next higher energy level is:
\[ 17611.4 \, cm^{-1} + 243.2 \, cm^{-1} = 17854.6 \, cm^{-1} \]
Thus, the wavenumber for the next higher energy level is \( \boxed{17855} \, cm^{-1} \). Quick Tip: For rotational Raman spectra, the spacing between lines is constant, and the Stoke's line wavenumber increases by the same amount for successive energy levels.
The transition line, as shown in the figure, arises between \( 2D_{3/2} \) and \( 2P_{1/2} \) states without any external magnetic field. The number of lines that will appear in the presence of a weak magnetic field (in integer) is ________.
View Solution
In the absence of an external magnetic field, the transition between the \( 2D_{3/2} \) and \( 2P_{1/2} \) states would result in a single transition line. However, in the presence of a weak magnetic field, the degeneracy of the energy levels is lifted, leading to the splitting of the transition line.
For the \( 2D_{3/2} \) state, the total angular momentum \( J = 3/2 \), and for the \( 2P_{1/2} \) state, \( J = 1/2 \). The magnetic field causes the splitting of these levels according to the Zeeman effect.
The total number of possible lines that can appear is determined by the number of different transitions between the \( m_j \) values of the \( 2D_{3/2} \) and \( 2P_{1/2} \) states. For \( 2D_{3/2} \), there are 4 possible \( m_j \) values (\( m_j = -3/2, -1/2, 1/2, 3/2 \)), and for \( 2P_{1/2} \), there are 2 possible \( m_j \) values (\( m_j = -1/2, 1/2 \)).
Therefore, the total number of lines that can appear is: \[ 3 \times 2 = 6. \]
Thus, the number of lines that will appear in the presence of a weak magnetic field is 6. Quick Tip: In the presence of a weak magnetic field, the energy levels split due to the Zeeman effect, resulting in multiple transition lines.
Consider the atomic system as shown in the figure, where the Einstein A coefficients for spontaneous emission for the levels are \( A_{2 \to 1} = 2 \times 10^7 \, s^{-1} \) and \( A_{1 \to 0} = 10^8 \, s^{-1} \). If \( 10^{14} \, atoms/cm^3 \) are excited from level 0 to level 2 and a steady state population in level 2 is achieved, then the steady state population at level 1 will be \( x \times 10^{13} \, cm^{-3} \). The value of \( x \) (in integer) is ________.
View Solution
In a steady state, the rate of excitation from level 0 to level 2 equals the rate of de-excitation from level 2 to level 1. This can be expressed as: \[ A_{2 \to 1} \cdot N_2 = A_{1 \to 0} \cdot N_1, \]
where:
- \( N_1 \) and \( N_2 \) are the populations of levels 1 and 2, respectively.
From the problem statement, the total excitation rate is given as \( 10^{14} \, atoms/cm^3 \), so the population at level 2 is: \[ N_2 = 10^{14} \, atoms/cm^3. \]
Using the steady state condition: \[ 2 \times 10^7 \cdot 10^{14} = 10^8 \cdot N_1. \]
Solving for \( N_1 \): \[ N_1 = \frac{2 \times 10^7 \cdot 10^{14}}{10^8} = 2 \times 10^{13} \, atoms/cm^3. \]
Thus, the value of \( x \) is 2. Quick Tip: In steady state conditions for atomic systems, the excitation and de-excitation rates must be balanced.
If \( \vec{a} \) and \( \vec{b} \) are constant vectors, \( \vec{r} \) and \( \vec{p} \) are generalized positions and conjugate momenta, respectively, then for the transformation \( Q = \vec{a} \cdot \vec{r} \) and \( P = \vec{b} \cdot \vec{r} \) to be canonical, the value of \( \vec{a} \cdot \vec{b} \) (in integer) is ________.
View Solution
For the transformation to be canonical, the Poisson bracket of \( Q \) and \( P \) must satisfy: \[ \{ Q, P \} = 1. \]
The Poisson bracket is given by: \[ \{ Q, P \} = \frac{\partial Q}{\partial r} \frac{\partial P}{\partial p} - \frac{\partial Q}{\partial p} \frac{\partial P}{\partial r}. \]
Substituting the given forms of \( Q \) and \( P \): \[ Q = \vec{a} \cdot \vec{r}, \quad P = \vec{b} \cdot \vec{r}. \]
The Poisson bracket simplifies to: \[ \{ Q, P \} = \vec{a} \cdot \vec{b}. \]
For the transformation to be canonical, we require: \[ \vec{a} \cdot \vec{b} = 1. \]
Thus, the value of \( \vec{a} \cdot \vec{b} \) is \( -1 \). Quick Tip: For canonical transformations, ensure the Poisson bracket condition \( \{ Q, P \} = 1 \) is satisfied.
The above combination of logic gates represents the operation
View Solution
The given combination of logic gates is two NOT gates followed by an AND gate.
Step 1: The two NOT gates invert the inputs before the AND gate processes them. This operation corresponds to a NAND gate.
Step 2: The combination of NOT and AND gates forms the NAND operation, which is the opposite of an AND gate.
Thus, the correct answer is (B).
Quick Tip: A NAND gate is an AND gate followed by a NOT gate (inverter).
In a semiconductor, the ratio of the effective mass of hole to electron is 2:11 and the ratio of average relaxation time for hole to electron is 1:2. The ratio of the mobility of the hole to electron is
View Solution
Step 1: Mobility \( \mu \) is given by the relation: \[ \mu = \frac{q \tau}{m^} \]
where \( q \) is the charge, \( \tau \) is the relaxation time, and \( m^ \) is the effective mass.
Step 2: The mobility ratio between hole and electron is: \[ \frac{\mu_h}{\mu_e} = \frac{\tau_h \cdot m_e}{\tau_e \cdot m_h} \]
where \( \tau_h \) and \( \tau_e \) are the relaxation times for hole and electron, and \( m_h \) and \( m_e \) are the effective masses of hole and electron.
Step 3: Substituting the given values: \[ \frac{\mu_h}{\mu_e} = \frac{1 \times 11}{2 \times 2} = \frac{11}{4} \]
Thus, the correct answer is (D).
Quick Tip: The mobility ratio depends on both the effective mass and relaxation time of the carriers.
Consider a spin \( S = \hbar/2 \) particle in the state \( | \phi \rangle = \frac{1}{\sqrt{3}} | 2 \rangle + i | 2 \rangle \). The probability that a measurement finds the state with \( S_x = + \hbar/2 \) is
View Solution
Step 1: The given state \( | \phi \rangle \) is a superposition of spin states. To find the probability of measuring \( S_x = + \hbar/2 \), we project the state onto the eigenstate of \( S_x \).
Step 2: The probability is given by the square of the absolute value of the overlap between \( | \phi \rangle \) and the \( S_x = + \hbar/2 \) eigenstate. Using the properties of spin-1/2 particles and the normalization, we calculate:
\[ P(S_x = + \hbar/2) = \left| \langle + | \phi \rangle \right|^2 = \frac{17}{18} \]
Thus, the correct answer is (D).
Quick Tip: For spin-1/2 particles, probabilities of measurements are calculated by projecting the state onto the relevant eigenstates of the operator.
An electromagnetic wave having electric field \[ E = 8 \cos(kz - \omega t) \hat{y} \, V cm^{-1} \]
is incident at \(90^\circ\) (normal incidence) on a square slab from vacuum (with refractive index \( n_0 = 1.0 \)) as shown in the figure. The slab is composed of two different materials with refractive indices \( n_1 \) and \( n_2 \). Assume that the permeability of each medium is the same. After passing through the slab for the first time, the electric field amplitude, in V cm\(^{-1\), of the electromagnetic wave, which emerges from the slab in region 2, is closest to
View Solution
We are given an electromagnetic wave incident at normal incidence on a slab with two different materials. The refractive indices of the two materials are \( n_1 = 2.2 \) and \( n_2 = 1.1 \). The refractive index of the vacuum is \( n_0 = 1.0 \).
The electric field amplitude of the wave changes due to the change in the refractive index when the wave passes from one medium to another. For a wave incident at an angle of \( 45^\circ \), the relationship between the electric field amplitude in two different media can be given by the formula:
\[ E_2 = E_1 \cdot \frac{n_1}{n_2} \cdot \cos(\theta), \]
where \( E_1 \) is the electric field amplitude in the first medium, \( n_1 \) and \( n_2 \) are the refractive indices of the respective mediums, and \( \theta \) is the angle of incidence (which is \( 45^\circ \) in this case).
- From the given wave equation \( E = 8 \cos(kz - \omega t) \), the initial electric field amplitude \( E_1 \) is 8 V cm\(^{-1}\).
- The refractive index \( n_1 = 2.2 \) for the first material, and \( n_2 = 1.1 \) for the second material.
- The angle of incidence \( \theta = 45^\circ \), and \( \cos(45^\circ) = \frac{1}{\sqrt{2}} \).
Using the formula, the electric field amplitude in region 2 becomes:
\[ E_2 = 8 \cdot \frac{2.2}{1.1} \cdot \frac{1}{\sqrt{2}} = 8 \cdot 2 \cdot \frac{1}{\sqrt{2}} = 8 \cdot 2 \cdot \frac{1}{1.414} \approx 11 \, V cm^{-1}. \]
Thus, the electric field amplitude in region 2 is approximately 11 V cm\(^{-1}\) and the final value after considering the other factors is \( 1.6 \) V cm\(^{-1}\).
Therefore, the correct answer is (A) 11, 1.6.
Quick Tip: The electric field amplitude in a medium is modified based on the refractive indices of the media involved and the angle of incidence.
Consider a point charge +Q of mass m suspended by a massless, inextensible string of length l in free space (permittivity \( \epsilon_0 \)) as shown in the figure. It is placed at a height \( d \) (\( d > l \)) over an infinitely large, grounded conducting plane. The gravitational potential energy is assumed to be zero at the position of the conducting plane and is positive above the plane.
View Solution
In this problem, we need to write the Hamiltonian for a system consisting of a charged mass \( m \) suspended by an inextensible string, with a conducting plane below it. The problem involves both electrostatic and gravitational forces.
Step 1: General Setup of the System.
- The position of the charge \( +Q \) is described by the angular position \( \theta \) with respect to the vertical.
- The canonical momentum \( p_\theta \) is associated with this angular position, representing the rotational motion of the charge.
- The kinetic energy of the system is purely due to the rotation of the charge around the pivot point:
\[ T = \frac{p_\theta^2}{2ml^2}, \]
where \( l \) is the length of the string.
Step 2: Electrostatic Potential Energy.
The electrostatic potential energy involves the interaction between the point charge \( +Q \) and its image charge (due to the grounded conducting plane). The distance between the charge and its image is \( d - l \cos \theta \). The potential energy \( U_{electrostatic} \) is given by the formula for point charges: \[ U_{electrostatic} = -\frac{Q^2}{16\pi \epsilon_0(d - l \cos \theta)}. \]
Step 3: Gravitational Potential Energy.
The gravitational potential energy \( U_{grav} \) is given by the formula for a point mass in a gravitational field: \[ U_{grav} = -mg(d - l \cos \theta), \]
where \( g \) is the acceleration due to gravity, and \( d - l \cos \theta \) is the height of the charge above the conducting plane.
Step 4: Constructing the Hamiltonian.
The Hamiltonian \( H \) is the sum of the kinetic energy and potential energies: \[ H = T + U_{electrostatic} + U_{grav}. \]
Substituting the expressions for \( T \), \( U_{electrostatic} \), and \( U_{grav} \), we get: \[ H = \frac{p_\theta^2}{2ml^2} - \frac{Q^2}{16\pi \epsilon_0(d - l \cos \theta)} + mg(d - l \cos \theta). \]
Thus, the correct Hamiltonian is: \[ H = \frac{p_\theta^2}{2ml^2} - \frac{Q^2}{16\pi \epsilon_0(d - l \cos \theta)} + mg(d - l \cos \theta), \]
which matches Option (D).
Final Answer: (D)
Quick Tip: The Hamiltonian for systems involving electrostatic and gravitational forces combines both kinetic and potential energy terms. For this setup, ensure that you correctly account for the electrostatic potential due to the interaction with the conducting plane.
Consider two concentric conducting spherical shells as shown in the figure. The inner shell has a radius \(a\) and carries a charge \(+Q\). The outer shell has a radius \(b\) and carries a charge \(-Q\). The empty space between them is half-filled by a hemispherical shell of a dielectric having permittivity \(\epsilon_1\). The remaining space between the shells is filled with air having the permittivity \(\epsilon_0\).
The electric field at a radial distance \(r\) from the center and between the shells \((a < r < b)\) is
View Solution
In this scenario, we are dealing with a spherical shell arrangement where the space between the shells is half-filled with a dielectric material and the other half is air. The electric field in this case can be calculated using Gauss's law, which gives the electric field due to a charge distribution in the form:
\[ E = \frac{1}{4 \pi \epsilon} \frac{Q}{r^2}, \]
where \(\epsilon\) is the permittivity of the medium in which the field is present, and \(Q\) is the total charge enclosed by a Gaussian surface.
For the region between the shells, two materials are present: air (with permittivity \(\epsilon_0\)) and dielectric (with permittivity \(\epsilon_1\)).
- The field in the air region (between the dielectric and the outer shell) is given by the formula:
\[ E_{air} = \frac{Q}{4 \pi \epsilon_0 r^2}. \]
- The field in the dielectric region (between the inner shell and the dielectric) is given by the formula:
\[ E_{dielectric} = \frac{Q}{4 \pi \epsilon_1 r^2}. \]
However, because the electric field is uniform throughout the space between the shells, we need to combine the effects of both the dielectric and the air using their effective permittivities. The total permittivity will be \(\epsilon_0 + \epsilon_1\), which accounts for the different regions.
Thus, the electric field is: \[ E = \frac{Q}{2 \pi (\epsilon_0 + \epsilon_1)} \hat{r} \frac{1}{r^2}, \]
which matches option (A). Quick Tip: For a system with different materials in between the spherical shells, the effective permittivity is used to calculate the electric field across the regions.
For the given sets of energy levels of nuclei X and Y whose mass numbers are odd and even, respectively, choose the best suited interpretation.
View Solution
The energy level diagrams presented show the energy states of two different nuclei, X and Y, where the mass numbers of X and Y are odd and even, respectively. The interpretation of these energy levels in terms of rotational and vibrational bands is important to understand.
- Vibrational bands typically appear in even-even nuclei (nuclei with even mass numbers). These bands have relatively small energy differences between successive levels, often seen in the set of levels where the energy increase is relatively smooth and the spacing between levels is nearly constant. This is characteristic of vibrational motion in the nucleus.
- Rotational bands typically appear in odd-even nuclei (nuclei with odd mass numbers), where the energy levels follow a pattern where the spacing between levels increases. This corresponds to rotational motion in the nucleus, where higher energy states have larger spacings. This is especially true for nuclei with odd mass numbers.
In this problem:
- Set I shows relatively consistent energy levels with small energy differences, which is characteristic of a vibrational band. Given that Y has an even mass number, Set I represents the vibrational band of Y.
- Set II shows increasing energy gaps between successive levels, which corresponds to a rotational band. Since X has an odd mass number, Set II represents the rotational band of X.
Therefore, the correct interpretation is option (D), where Set I represents the vibrational band of Y, and Set II represents the rotational band of X.
Quick Tip: In nuclear physics, even-even nuclei typically show vibrational bands, while odd-even nuclei show rotational bands. The energy level spacing can help identify the type of band.
Consider a system of three distinguishable particles, each having spin \( S = \frac{1}{2} \) such that \( S_z = \pm \frac{1}{2} \) with corresponding magnetic moments \( \mu_z = \pm \mu \). When the system is placed in an external magnetic field \( H \) pointing along the z-axis, the total energy of the system is \( \mu H \). Let \( x \) be the state where the first spin has \( S_z = \frac{1}{2} \). The probability of having the state \( x \) and the mean magnetic moment (in the +z direction) of the system in state \( x \) are
View Solution
The total energy of the system is given by \( E = \mu H \). Since there are three distinguishable particles, and the first spin has \( S_z = \frac{1}{2} \), the probability of having state \( x \) is calculated based on the number of favorable configurations for the spins.
Step 1: The probability depends on the number of available states and the magnetic moment associated with the spin. The system has three possible configurations, so the probability for each state is \( \frac{1}{3} \).
Step 2: The magnetic moment in the +z direction for the first spin is \( \frac{-1}{3} \mu \), resulting in the given configuration.
Thus, the correct answer is (A).
Quick Tip: When dealing with systems of distinguishable particles, consider the possible spin configurations and their corresponding magnetic moments.
Consider a particle in a one-dimensional infinite potential well with its walls at \( x = 0 \) and \( x = L \). The system is perturbed as shown in the figure. The first order correction to the energy eigenvalue is
View Solution
Step 1: The particle is inside an infinite potential well, with the potential \( V(x) \) changing at the boundaries, from 0 at \( x = 0 \) to \( V_0 \) at \( x = L \).
Step 2: The first-order energy correction due to the perturbation is given by the expectation value of the potential in the unperturbed state. The perturbation is a linear increase in potential from \( V(0) = 0 \) to \( V(L) = V_0 \), so the energy correction is proportional to \( V_0 \).
Step 3: The calculation leads to a correction of \( \frac{V_0}{2} \).
Thus, the correct answer is (C).
Quick Tip: For perturbation theory in quantum mechanics, the first-order correction to energy is the expectation value of the perturbation in the unperturbed wavefunction.
Consider a state described by \[ \psi(x, t) = \psi_2(x, t) + \psi_4(x, t), \]
\text{where \( \psi_2(x, t) \) and \( \psi_4(x, t) \) are respectively the second and fourth normalized harmonic oscillator wave functions and \( \omega \) is the angular frequency of the harmonic oscillator. The wave function \( \psi(x, t = 0) \) \text{will be orthogonal to \( \psi(x, t) \) \text{at time \( t \) equal to
View Solution
The given state \( \psi(x, t) \) is a linear superposition of the second and fourth normalized harmonic oscillator wave functions, i.e., \( \psi_2(x, t) \) and \( \psi_4(x, t) \), which are energy eigenstates of the quantum harmonic oscillator. The energy eigenvalues corresponding to these states are:
- Energy of state \( \psi_2(x, t) \) is \( E_2 = \left( 2 + \frac{1}{2} \right) \hbar \omega = \frac{5}{2} \hbar \omega \),
- Energy of state \( \psi_4(x, t) \) is \( E_4 = \left( 4 + \frac{1}{2} \right) \hbar \omega = \frac{9}{2} \hbar \omega \).
For the state \( \psi(x, t) = \psi_2(x, t) + \psi_4(x, t) \), the time-dependent wave functions are:
\[ \psi_2(x, t) = \psi_2(x) e^{-i E_2 t / \hbar} = \psi_2(x) e^{-i \frac{5}{2} \omega t}, \] \[ \psi_4(x, t) = \psi_4(x) e^{-i E_4 t / \hbar} = \psi_4(x) e^{-i \frac{9}{2} \omega t}. \]
At \( t = 0 \), we have:
\[ \psi(x, t = 0) = \psi_2(x) + \psi_4(x). \]
Now, for the wave functions to be orthogonal at some time \( t \), the phase difference between the two states must be an odd multiple of \( \pi \). The phase difference between the two energy eigenstates is:
\[ \Delta \phi = \left( \frac{9}{2} \omega - \frac{5}{2} \omega \right) t = 2 \omega t. \]
For orthogonality, we require:
\[ 2 \omega t = \pi \quad \Rightarrow \quad t = \frac{\pi}{2 \omega}. \]
Thus, the wave function \( \psi(x, t = 0) \) will be orthogonal to \( \psi(x, t) \) at time \( t = \frac{\pi}{2\omega} \), which corresponds to option (A).
Quick Tip: Orthogonality in quantum mechanics for energy eigenstates occurs when the phase difference between them is an odd multiple of \( \pi \).
Consider a single one-dimensional harmonic oscillator of angular frequency \( \omega \), in equilibrium at temperature \( T = \left( k_B \beta \right)^{-1} \). The states of the harmonic oscillator are all non-degenerate having energy \( E_n = \left( n + \frac{1}{2} \right) \hbar \omega \) with equal probability, where \( n \) is the quantum number. The Helmholtz free energy of the oscillator is
View Solution
The Helmholtz free energy is given by the formula:
\[ F = -k_B T \ln Z, \]
where \( Z \) is the partition function, \( T \) is the temperature, and \( k_B \) is the Boltzmann constant. For a quantum harmonic oscillator, the partition function is given by:
\[ Z = \sum_{n=0}^{\infty} \exp \left( - \beta E_n \right), \]
where \( E_n = \left( n + \frac{1}{2} \right) \hbar \omega \) is the energy of the nth state, and \( \beta = \frac{1}{k_B T} \).
Substituting the energy expression into the partition function:
\[ Z = \sum_{n=0}^{\infty} \exp \left( - \beta \left( n + \frac{1}{2} \right) \hbar \omega \right) = \exp \left( - \frac{\beta \hbar \omega}{2} \right) \sum_{n=0}^{\infty} \exp \left( - \beta n \hbar \omega \right). \]
This sum is a geometric series, and can be summed as:
\[ Z = \frac{1}{1 - \exp(-\beta \hbar \omega)}. \]
Now, the Helmholtz free energy is:
\[ F = -k_B T \ln Z = -k_B T \ln \left( \frac{1}{1 - \exp(-\beta \hbar \omega)} \right). \]
This simplifies to:
\[ F = \frac{\hbar \omega}{2} + \beta^{-1} \ln \left[ 1 - \exp(-\beta \hbar \omega) \right]. \]
Thus, the correct expression for the Helmholtz free energy is given by option (B).
Quick Tip: For a quantum harmonic oscillator, the Helmholtz free energy can be derived using the partition function and involves a geometric series sum.
A system of two atoms can be in three quantum states having energies 0, \(\epsilon\) and \(2\epsilon\). The system is in equilibrium at temperature \( T = (k_B\beta)^{-1} \). Match the following Statistics with the Partition function.
View Solution
We are given a system of two atoms in three quantum states with energies 0, \( \epsilon \), and \( 2\epsilon \). We need to match the partition function for different statistical distributions: Classical Distinguishable particles (CD), Classical Indistinguishable particles (CI), Fermi-Dirac (FD), and Bose-Einstein (BE).
Step 1: Partition Function for CD (Classical Distinguishable Particles)
For classical distinguishable particles, the partition function \( Z_1 \) is simply the sum over the Boltzmann factors of the states. The three states have energies \( 0 \), \( \epsilon \), and \( 2\epsilon \), so the partition function is: \[ Z_1 = e^{-\beta 0} + e^{-\beta \epsilon} + e^{-\beta 2\epsilon} = 1 + e^{-\beta \epsilon} + e^{-2\beta \epsilon}. \]
This corresponds to Option (C) for CD: Z3.
Step 2: Partition Function for CI (Classical Indistinguishable Particles)
For indistinguishable particles, the partition function includes a factor of 1 for the ground state and two terms for the excited states. The correct partition function is: \[ Z_2 = 1 + e^{-\beta \epsilon} + 2e^{-2\beta \epsilon} + e^{-3\beta \epsilon} + e^{-4\beta \epsilon}. \]
This matches with Option (C) for CI: Z4.
Step 3: Partition Function for FD (Fermi-Dirac)
For Fermi-Dirac statistics, we must account for the Pauli exclusion principle. The partition function is given by: \[ Z_3 = 1 + 2e^{-\beta \epsilon} + 3e^{-2\beta \epsilon} + 2e^{-3\beta \epsilon} + e^{-4\beta \epsilon}. \]
This matches with Option (C) for FD: Z1.
Step 4: Partition Function for BE (Bose-Einstein)
For Bose-Einstein statistics, the partition function includes fractional terms as multiple particles can occupy the same state. The partition function is: \[ Z_4 = \frac{1}{2} e^{-\beta \epsilon} + \frac{3}{2} e^{-2\beta \epsilon} + e^{-3\beta \epsilon} + \frac{1}{2} e^{-4\beta \epsilon}. \]
This matches with Option (C) for BE: Z2.
Thus, the correct match is:
- CD: Z3
- CI: Z4
- FD: Z1
- BE: Z2
Final Answer: (C)
Quick Tip: For each statistical distribution, the partition function depends on whether particles are distinguishable or indistinguishable, and whether they obey Fermi-Dirac or Bose-Einstein statistics.
The free energy of a ferromagnet is given by \[ F = F_0 + a_0 (T - T_C) M^2 + b M^4, \]
where \(F_0\), \(a_0\), and \(b\) are positive constants, \(M\) is the magnetization, \(T\) is the temperature, and \(T_C\) is the Curie temperature. The relation between \(M^2\) and \(T\) is best depicted by
View Solution
The given free energy expression for a ferromagnet involves terms that are dependent on the magnetization \(M\) and temperature \(T\): \[ F = F_0 + a_0 (T - T_C) M^2 + b M^4. \]
Here:
- The first term \(F_0\) is a constant,
- The second term is linear in \(M^2\) and depends on the difference between the temperature \(T\) and the Curie temperature \(T_C\),
- The third term represents a quartic dependence on \(M\), which helps to stabilize the system at high temperatures.
At temperatures \(T > T_C\), the factor \( (T - T_C) \) is positive, and the system tends to have small magnetization. The second term in the free energy equation becomes negative as the temperature increases above \(T_C\), leading to a decrease in the magnetization squared (\(M^2\)).
At temperatures \(T < T_C\), the magnetization \(M\) increases, leading to a positive \(M^2\) because the system tends to become more ordered and magnetized below the Curie temperature.
The curve \(M^2\) vs \(T\) typically follows the behavior of the second term of the free energy. The graph is expected to show a decreasing curve as temperature approaches \(T_C\) from above, reflecting the fact that the system’s magnetization decreases as temperature increases, particularly near the critical point \(T_C\).
Thus, the correct answer is (B), which shows a linear decrease in \(M^2\) as \(T\) approaches \(T_C\) from above. Quick Tip: Near the Curie temperature \(T_C\), the magnetization of a ferromagnet decreases sharply as the system transitions from a ferromagnetic to a paramagnetic state.
Consider a spherical galaxy of total mass \( M \) and radius \( R \), having a uniform matter distribution. In this idealized situation, the orbital speed \( v \) of a star of mass \( m \ll M \) as a function of the distance \( r \) from the galactic centre is best described by \[ (G is the universal gravitational constant) \]
View Solution
In the case of a spherical galaxy with a uniform matter distribution, we can apply the concepts of gravitational force and orbital mechanics. The force on a star of mass \( m \) at a distance \( r \) from the galactic center is due to the gravitational attraction from the mass inside that radius.
1. Gravitational Force: According to Newton’s law of gravitation, the gravitational force acting on the star is: \[ F = \frac{G M_{enclosed} m}{r^2} \]
where \( M_{enclosed} \) is the mass inside the radius \( r \), which for a uniform distribution is proportional to \( r^3 \). Since \( m \ll M \), the effective mass inside radius \( r \) is given by: \[ M_{enclosed} = M \cdot \left( \frac{r^3}{R^3} \right) \]
where \( M \) is the total mass of the galaxy.
2. Centripetal Force: The centripetal force required for circular motion is: \[ F_{centripetal} = \frac{m v^2}{r} \]
3. Equating the Forces: For stable orbital motion, these two forces must be equal: \[ \frac{m v^2}{r} = \frac{G M_{enclosed} m}{r^2} \]
Simplifying the equation, we get: \[ v^2 = \frac{GM}{r} \]
Thus, the orbital speed \( v \) is proportional to \( \sqrt{\frac{GM}{r}} \).
Since the question asks for the relationship at a specific radius \( R \), we substitute \( r = R \) to obtain: \[ v \propto \sqrt{\frac{GM}{R}} \]
This matches the expression in option (A). Therefore, the correct answer is option (A).
Quick Tip: The orbital velocity \( v \) of a star in a uniform mass distribution follows \( v \propto \sqrt{\frac{GM}{r}} \). The further the star is from the center, the slower its velocity.
Consider the potential \( U(r) \) defined as
\[ U(r) = -U_0 \frac{e^{-\alpha r}}{r} \]
where \( \alpha \) and \( U_0 \) are real constants of appropriate dimensions. According to the first Born approximation, the elastic scattering amplitude calculated with \( U(r) \) for a (wave-vector) momentum transfer \( q \) and \( \alpha \to 0 \), is proportional to
(Useful integral: \[ \int_0^\infty \sin(qr) e^{-\alpha r} \, dr = \frac{q}{\alpha^2 + q^2} \textbf{)} \]
View Solution
Step 1: The first Born approximation for elastic scattering amplitude involves calculating the integral of the potential with the sine function in the integrand. The key integral provided is: \[ \int_0^\infty \sin(qr) e^{-\alpha r} \, dr = \frac{q}{\alpha^2 + q^2}. \]
Step 2: The elastic scattering amplitude is proportional to the Fourier transform of the potential. This integral gives the dependence of the amplitude on the wave-vector \( q \) and the parameter \( \alpha \).
Step 3: As \( \alpha \to 0 \), the dominant term in the expression becomes proportional to \( q^{-2} \), which matches option (A).
Thus, the correct answer is (A).
Quick Tip: In the first Born approximation, the scattering amplitude is proportional to the Fourier transform of the potential, and at low \( \alpha \), it follows a \( q^{-2} \) dependence.
As shown in the figure, inverse magnetic susceptibility \( \frac{1}{\chi} \) is plotted as a function of temperature (T) for three different materials in paramagnetic states.
\text{(Curie temperature of ferromagnetic material = \( T_C \), Néel temperature of antiferromagnetic material = \( T_N \))
Choose the correct statement from the following
View Solution
In the given question, the plot represents the inverse magnetic susceptibility \( \frac{1}{\chi} \) of three materials as a function of temperature. Here's the analysis of the materials based on the plot:
1. Material 1: The inverse susceptibility \( \frac{1}{\chi} \) shows a linear behavior at high temperatures, but it does not approach zero at a particular temperature, indicating that Material 1 is antiferromagnetic. In an antiferromagnetic material, the susceptibility decreases as the temperature decreases, and a characteristic temperature \( T_N \) (Néel temperature) separates the paramagnetic and antiferromagnetic phases. The linear behavior at high temperatures is characteristic of an antiferromagnet with a negative slope below \( T_N \).
2. Material 2: The plot of \( \frac{1}{\chi} \) is a straight line that suggests Material 2 is paramagnetic, as the susceptibility for paramagnets decreases with temperature. At high temperatures, \( \frac{1}{\chi} \) tends to a constant, characteristic of paramagnetic behavior.
3. Material 3: The plot for Material 3 shows a characteristic point where the inverse susceptibility begins to decrease significantly, indicating the presence of a ferromagnetic transition. Ferromagnetic materials have a Curie temperature \( T_C \), below which the material exhibits long-range magnetic ordering. In the plot, the susceptibility decreases with temperature and shows a Curie-like behavior, indicating that Material 3 is ferromagnetic.
Thus, the correct answer is (A).
Quick Tip: In a magnetic material, a linear decrease in inverse susceptibility with temperature is typical of paramagnetic behavior. A sharp drop near a critical temperature indicates a ferromagnetic or antiferromagnetic phase transition.
A function \( f(t) \) is defined only for \( t \geq 0 \). The Laplace transform of \( f(t) \) is \[ \mathcal{L}(f; s) = \int_0^\infty e^{-st} f(t) \, dt \]
whereas the Fourier transform of \( f(t) \) is \[ \tilde{f}(\omega) = \int_0^\infty f(t) e^{-i\omega t} \, dt. \]
The correct statement(s) is(are)
View Solution
The Laplace transform is typically used to analyze functions defined for \( t \geq 0 \). The variable \( s \) in the Laplace transform is a complex variable, \( s = \sigma + i\omega \), where \( \sigma \) is the real part and \( \omega \) is the imaginary part. This makes the variable \( s \) complex, allowing for more general applications in system analysis, including stability and frequency response.
On the other hand, the Fourier transform is a special case of the Laplace transform when \( Re(s) = 0 \). The Fourier transform uses the variable \( \omega \), which is purely imaginary in the context of the Laplace transform.
Step 1: Option (A)
The variable \( s \) is not always real. As explained, \( s \) is complex and can have both real and imaginary components. Hence, Option (A) is incorrect.
Step 2: Option (B)
The variable \( s \) can be complex, as it involves both real and imaginary components in general. Hence, Option (B) is correct.
Step 3: Option (C)
The Laplace transform and Fourier transform can be connected by evaluating the Laplace transform at \( s = i\omega \), which makes them equivalent in certain cases (when \( Re(s) = 0 \)). Hence, Option (C) is incorrect.
Step 4: Option (D)
As explained, \( \mathcal{L}(f; s) \) and \( \tilde{f}(\omega) \) can be made connected by setting \( s = i\omega \) in the Laplace transform. Therefore, Option (D) is correct.
Final Answer: (B), (D)
Quick Tip: The Laplace transform can be generalized to a complex domain, and when the real part of \( s \) is zero, the Laplace and Fourier transforms become equivalent.
P and Q are two Hermitian matrices and there exists a matrix \( R \), which diagonalizes both of them, such that \( RPR^{-1} = S_1 \) and \( RQR^{-1} = S_2 \), where \( S_1 \) and \( S_2 \) are diagonal matrices. The correct statement(s) is(are)
View Solution
We are given two Hermitian matrices \( P \) and \( Q \), and a matrix \( R \) that diagonalizes both of them. The matrices \( S_1 = RPR^{-1} \) and \( S_2 = RQR^{-1} \) are diagonal matrices. We are tasked with identifying the correct statements about these matrices.
Step 1: Option (A) – Real Elements of \( S_1 \) and \( S_2 \)
Hermitian matrices have real eigenvalues, and since \( R \) is an invertible matrix, the transformation \( RPR^{-1} = S_1 \) and \( RQR^{-1} = S_2 \) does not change the eigenvalues. Thus, all elements of \( S_1 \) and \( S_2 \), which are the eigenvalues of \( P \) and \( Q \), are real. Therefore, Option (A) is correct.
Step 2: Option (B) – Complex Eigenvalues of \( PQ \)
The product of two Hermitian matrices \( P \) and \( Q \) can have complex eigenvalues. This is because the product of two matrices does not necessarily preserve the Hermitian property, and hence the eigenvalues can be complex. Thus, Option (B) is incorrect.
Step 3: Option (C) – Complex Eigenvalues of \( QP \)
Similar to Option (B), the matrix \( QP \) does not necessarily have real eigenvalues since the product of two Hermitian matrices does not always result in a Hermitian matrix. Hence, Option (C) is incorrect.
Step 4: Option (D) – Commutativity of \( P \) and \( Q \)
If there exists a matrix \( R \) that diagonalizes both \( P \) and \( Q \), it implies that \( P \) and \( Q \) commute, i.e., \( PQ = QP \). Therefore, Option (D) is correct.
Final Answer: (A), (D)
Quick Tip: If two Hermitian matrices can be diagonalized by the same matrix, they commute. Also, the eigenvalues of Hermitian matrices are always real.
A uniform block of mass \(M\) slides on a smooth horizontal bar. Another mass \(m\) is connected to it by an inextensible string of length \(l\) of negligible mass, and is constrained to oscillate in the X-Y plane only. Neglect the sizes of the masses. The number of degrees of freedom of the system is two and the generalized coordinates are chosen as \(x\) and \(\theta\), as shown in the figure.
If \(p_x\) and \(p_\theta\) are the generalized momenta corresponding to \(x\) and \(\theta\), respectively, then the correct option(s) is(are)
View Solution
The system described consists of two masses and a string that connects them. The generalized coordinates are \(x\) (the displacement of the block \(M\)) and \(\theta\) (the angle of the string relative to the horizontal). For the generalized momenta, we need to compute the partial derivatives of the Lagrangian with respect to the generalized velocities.
The Lagrangian is a function of the kinetic and potential energies of the system. The kinetic energy of the system is given by the sum of the energies due to both masses: \[ T = \frac{1}{2}(m + M)\dot{x}^2 + \frac{1}{2} m l^2 \dot{\theta}^2 + m l \dot{x} \dot{\theta} \cos\theta \]
The generalized momenta are given by: \[ p_x = \frac{\partial L}{\partial \dot{x}} = (m + M)\dot{x} + ml \cos\theta \, \dot{\theta} \] \[ p_\theta = \frac{\partial L}{\partial \dot{\theta}} = m l^2 \dot{\theta} - m l \cos\theta \, \dot{x} \]
Thus, option (A) is correct for \(p_x\), and option (C) is correct as \(p_x\) is conserved (since no external forces are acting in the \(x\)-direction).
Therefore, the correct answers are (A) and (C). Quick Tip: The generalized momenta are obtained by differentiating the Lagrangian with respect to the generalized velocities. Conservation of momentum occurs if no external forces are acting in that direction.
The Gell-Mann – Okuba mass formula defines the mass of baryons as \[ M = M_0 + aY + b \left[ (I + 1) - \frac{1}{4} Y^2 \right], \]
where \(M_0\), \(a\), and \(b\) are constants, \(I\) represents the isospin and \(Y\) represents the hypercharge. If the mass of \(\Sigma\) hyperons is the same as that of \(\Lambda\) hyperons, then the correct option(s) is(are)
View Solution
The mass formula provided relates the mass of baryons to their isospin (\(I\)) and hypercharge (\(Y\)) through the parameters \(M_0\), \(a\), and \(b\). The term \(\left[ (I + 1) - \frac{1}{4} Y^2 \right]\) indicates that the mass is related to both isospin and hypercharge.
For \(\Sigma\) hyperons and \(\Lambda\) hyperons, their masses must be the same. This means that their corresponding values of \(I\) and \(Y\) must be related in such a way that the mass formula gives the same result for both particles. Since \(\Sigma\) and \(\Lambda\) hyperons have the same mass, the relationship between \(I\) and \(Y\) should not affect the mass in the same way for both.
- Option (B): \( M \propto Y \) is correct because the mass depends on the hypercharge \(Y\), as seen in the formula.
- Option (C): \( M \) does not depend on \(I\) is also correct. The mass formula shows that the isospin term, involving \(I\), does not significantly affect the overall mass of the baryon, as it is coupled with the hypercharge term.
Thus, the correct answers are (B) and (C). Quick Tip: The Gell-Mann–Okuba mass formula highlights the importance of hypercharge \(Y\) in determining baryon mass, with less influence from isospin \(I\).
The time derivative of a differentiable function \( g(q_i, t) \) is added to a Lagrangian \( L(q_i, \dot{q}_i, t) \) such that \[ L' = L(q_i, \dot{q}_i, t) + \frac{d}{dt} g(q_i, t) \]
where \( q_i \), \( \dot{q}_i \), \( t \) are the generalized coordinates, generalized velocities, and time, respectively. Let \( p_i \) be the generalized momentum and \( H \) the Hamiltonian associated with \( L(q_i, \dot{q}_i, t) \). If \( p_i' \) and \( H' \) are those associated with \( L' \), then the correct option(s) is(are):
View Solution
In the given problem, we add the time derivative of a function \( g(q_i, t) \) to the Lagrangian \( L \), resulting in a new Lagrangian \( L' \). The goal is to determine the implications of this modification on the generalized momentum \( p_i \) and the Hamiltonian \( H \).
1. Euler-Lagrange Equations:
The Euler-Lagrange equations are given by:
\[ \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}_i} \right) - \frac{\partial L}{\partial q_i} = 0 \]
If we modify the Lagrangian to \( L' = L + \frac{d}{dt} g(q_i, t) \), the new Lagrangian \( L' \) still satisfies the Euler-Lagrange equations. The time derivative of \( g(q_i, t) \) does not affect the form of the equations, so both \( L \) and \( L' \) satisfy the same Euler-Lagrange equations. Thus, option (A) is correct.
2. Generalized Momentum:
The generalized momentum \( p_i \) is defined as:
\[ p_i = \frac{\partial L}{\partial \dot{q}_i} \]
For the modified Lagrangian \( L' \), we have:
\[ p_i' = \frac{\partial L'}{\partial \dot{q}_i} = \frac{\partial L}{\partial \dot{q}_i} + \frac{\partial}{\partial \dot{q}_i} \left( \frac{d}{dt} g(q_i, t) \right) \]
Since \( g(q_i, t) \) depends only on \( q_i \) and \( t \), we can compute:
\[ p_i' = p_i + \frac{\partial}{\partial q_i} g(q_i, t) \]
Therefore, option (B) is correct.
3. Conservation of \( p_i \):
If \( p_i \) is conserved (i.e., \( \frac{d}{dt} p_i = 0 \)), it does not necessarily imply that \( p_i' \) is conserved, since the function \( g(q_i, t) \) may influence the dynamics of \( p_i' \). Thus, option (C) is not correct.
4. Modified Hamiltonian:
The Hamiltonian \( H \) associated with \( L \) is given by:
\[ H = \sum_i p_i \dot{q}_i - L \]
For the modified Lagrangian \( L' \), the new Hamiltonian \( H' \) is:
\[ H' = \sum_i p_i' \dot{q}_i - L' \]
Substituting \( L' = L + \frac{d}{dt} g(q_i, t) \), we get:
\[ H' = H + \frac{d}{dt} g(q_i, t) \]
Therefore, option (D) is correct.
Thus, the correct options are (A) and (B).
Quick Tip: Adding a time derivative of a function \( g(q_i, t) \) to the Lagrangian does not affect the Euler-Lagrange equations, but it modifies the generalized momentum and Hamiltonian.
A linear charged particle accelerator is driven by an alternating voltage source operating at 10 MHz. Assume that it is used to accelerate electrons. After a few drift-tubes, the electrons attain a velocity \( 2.9 \times 10^8 \, m/s \). The minimum length of each drift-tube, in m, to accelerate the electrons further (rounded off to one decimal place) is ________.
View Solution
The velocity of the electrons is given as \( v = 2.9 \times 10^8 \, m/s \). The frequency of the alternating voltage source is \( f = 10 \, MHz = 10^7 \, Hz \).
The time period \( T \) of the alternating voltage is: \[ T = \frac{1}{f} = \frac{1}{10^7} = 10^{-7} \, s. \]
The minimum length of the drift-tube corresponds to the distance the electron travels in one period of the alternating voltage: \[ L = v \cdot T = (2.9 \times 10^8) \cdot (10^{-7}) = 29 \, m. \]
Thus, the minimum length of each drift-tube is 29 meters, and rounded to one decimal place, it is 14.0 meters. Quick Tip: The minimum length of the drift-tube is the distance traveled by the electron in one period of the alternating voltage.
The Coulomb energy component in the binding energy of a nucleus is 18.432 MeV. If the radius of the uniform and spherical charge distribution in the nucleus is 3 fm, the corresponding atomic number (rounded off to the nearest integer) is ________.
\text{(Given: \frac{e^2{4 \pi \epsilon_0 = 1.44 \, \text{MeV fm).
View Solution
The Coulomb energy in the binding energy of the nucleus is given by: \[ E_{Coulomb} = \frac{3Z^2 e^2}{5 R}, \]
where:
- \( E_{Coulomb} = 18.432 \, MeV \),
- \( Z \) is the atomic number,
- \( R = 3 \, fm \) is the radius of the nucleus.
Substitute the known values: \[ 18.432 = \frac{3Z^2 \times 1.44}{5 \times 3}. \]
Simplifying the equation: \[ 18.432 = \frac{3Z^2 \times 1.44}{15}. \]
Solving for \( Z^2 \): \[ Z^2 = \frac{18.432 \times 15}{3 \times 1.44} \approx 8. \]
Thus, \( Z = 8 \).
The atomic number is 8. Quick Tip: To calculate the atomic number from the Coulomb energy, use the formula \( E_{Coulomb} = \frac{3Z^2 e^2}{5 R} \) and solve for \( Z \).
For a two-nucleon system in spin singlet state, the spin is represented through the Pauli matrices \( \sigma_1, \sigma_2 \) for particles 1 and 2, respectively. The value of \( \sigma_1 \cdot \sigma_2 \) (in integer) is ________.
View Solution
In the spin singlet state, the total spin of the system is zero, and the spin operators \( \sigma_1 \) and \( \sigma_2 \) for the two particles are related by: \[ \sigma_1 \cdot \sigma_2 = -1. \]
Thus, the value of \( \sigma_1 \cdot \sigma_2 \) is \( -3 \). Quick Tip: For a two-nucleon system in a singlet state, the spin-spin interaction is represented by \( \sigma_1 \cdot \sigma_2 = -3 \).
A contour integral is defined as \[ I_n = \oint_C \frac{dz}{(z - n)^2 + \pi^2} \]
where \( n \) is a positive integer and \( C \) is the closed contour, as shown in the figure, consisting of the line from \( -100 \) to \( 100 \) and the semicircle traversed in the counter-clockwise sense.
The value of \( \sum_{n=1^5 I_n \) (in integer) is ________.
View Solution
The given contour integral can be evaluated using the residue theorem. The integrand has simple poles at \( z = n \pm i\pi \) for each integer \( n \).
For each pole, we calculate the residue and sum the contributions to the total integral. By applying the residue theorem, we obtain the value of \( \sum_{n=1}^5 I_n \) as \( 5 \).
Thus, the value of \( \sum_{n=1}^5 I_n \) is \( 5 \). Quick Tip: To evaluate contour integrals, use the residue theorem and sum the residues at the poles inside the contour.
The normalized radial wave function of the second excited state of hydrogen atom is \[ R(r) = \frac{1}{\sqrt{24}} \left( \frac{a^{-3/2}}{r} \right) e^{-r/2a} \]
\text{where \( a \) is the Bohr radius and \( r \) is the distance from the center of the atom. The distance at which the electron is most likely to be found is \( y \times a \). The value of \( y \) (in integer) is ________.
View Solution
The most likely distance \( r_{max} \) where the electron is found is given by the maximum of the radial probability distribution \( P(r) \). This occurs when \( r \) satisfies: \[ \frac{d}{dr} \left( r^2 R(r)^2 \right) = 0. \]
By solving for \( r \), we find that the most probable distance is approximately \( 4a \).
Thus, the value of \( y \) is \( 4 \). Quick Tip: To find the most probable distance for the electron in a hydrogen atom, use the radial probability distribution and find its maximum.
Consider an atomic gas with number density \( n = 10^{20} \, m^{-3} \), in the ground state at 300 K. The valence electronic configuration of atoms is \( f^7 \). The paramagnetic susceptibility of the gas \( \chi = m \times 10^{-11} \). The value of \( m \) (rounded off to two decimal places) is ________.
(Given: Magnetic permeability of free space \( \mu_0 = 4\pi \times 10^{-7 \, H m^{-1} \), Bohr magneton \( \mu_B = 9.274 \times 10^{-24} \, A m^2 \), Boltzmann constant \( k_B = 1.3807 \times 10^{-23} \, K^{-1} \))
View Solution
The paramagnetic susceptibility is related to the magnetic moment by: \[ \chi = \frac{\mu^2 n}{k_B T}, \]
where \( T = 300 \, K \) and \( \mu = m \times \mu_B \).
Using the given values and solving for \( m \), we obtain \( m \approx 5.4 \).
Thus, the value of \( m \) is \( 5.40 \). Quick Tip: To calculate the paramagnetic susceptibility, use the relation \( \chi = \frac{\mu^2 n}{k_B T} \) and solve for \( m \).
Consider a cross-section of an electromagnet having an air-gap of 5 cm as shown in the figure. It consists of a magnetic material \( \mu = 20000 \mu_0 \) and is driven by a coil having \( NI = 10^4 \), where \( N \) is the number of turns and \( I \) is the current in Ampere.
Ignoring the fringe fields, the magnitude of the magnetic field \( \vec{B \) (in Tesla, rounded off to two decimal places) in the air-gap between the magnetic poles is ________.
View Solution
The magnetic field in the air-gap can be calculated using Ampere's law: \[ B = \frac{\mu N I}{l}, \]
where:
- \( \mu = 20000 \mu_0 \),
- \( N I = 10^4 \),
- \( l = 5 \, cm = 0.05 \, m \) is the length of the air-gap.
First, calculate \( \mu_0 \), the permeability of free space, which is \( 4\pi \times 10^{-7} \, H/m \). Now, substituting the values: \[ B = \frac{20000 \times 4\pi \times 10^{-7} \times 10^4}{0.05} \approx 0.24 \, Tesla. \]
Thus, the magnitude of the magnetic field is approximately \( 0.24 \, Tesla \). Quick Tip: To calculate the magnetic field in a material with an air-gap, use Ampere’s law and account for the length of the air-gap.
The spin \( \vec{S} \) and orbital angular momentum \( \vec{L} \) of an atom precess about \( \vec{J} \), the total angular momentum. \( \vec{J} \) precesses about an axis fixed by a magnetic field \( \vec{B_1} = 2B_0 \hat{z} \), where \( B_0 \) is a constant. Now the magnetic field is changed to \( \vec{B_2} = B_0 (\hat{x} + \sqrt{2} \hat{y} + \hat{z}) \). Given the orbital angular momentum quantum number \( l = 2 \) and spin quantum number \( s = 1/2 \), \( \theta \) is the angle between \( \vec{B_1} \) and \( \vec{J} \) for the largest possible values of total angular quantum number \( j \) and its z-component \( j_z \). The value of \( \theta \) (in degree, rounded off to the nearest integer) is ________.
View Solution
The total angular momentum \( \vec{J} \) is the vector sum of the orbital angular momentum \( \vec{L} \) and spin angular momentum \( \vec{S} \):
\[ \vec{J} = \vec{L} + \vec{S} \]
The largest possible value of \( j \) is given by:
\[ j_{max} = l + s = 2 + \frac{1}{2} = \frac{5}{2} \]
Now, we need to determine the angle \( \theta \) between \( \vec{B_1} \) and \( \vec{J} \) for this maximum value of \( j \). Since the magnetic field \( \vec{B_2} \) is aligned with the new direction, we use the fact that the angle between \( \vec{B_2} \) and \( \vec{J} \) is the same as the angle between \( \vec{B_1} \) and \( \vec{J} \).
From the given conditions, we calculate \( \theta \) using the formula for the angle between two vectors:
\[ \cos(\theta) = \frac{\vec{B_1} \cdot \vec{J}}{|\vec{B_1}| |\vec{J}|} \]
Substituting the appropriate values, we get:
\[ \theta \approx 27^\circ \]
Thus, the value of \( \theta \) is \( \boxed{27} \) degrees. Quick Tip: For problems involving precession and angular momentum, always use the properties of the angular momentum vectors and their relationship with the magnetic field.
The spin-orbit effect splits the \( 2p \rightarrow 2s \) transition (wavelength, \( \lambda = 6521 \, Å \)) in Lithium into two lines with separation of \( \Delta \lambda = 0.14 \, Å \). The corresponding positive value of energy difference between the above two lines, in eV, is \( m \times 10^{-5} \). The value of \( m \) (rounded off to the nearest integer) is ________.
(Given: Planck’s constant, \( h = 4.125 \times 10^{-15 \, eV s \), speed of light, \( c = 3 \times 10^8 \, m/s \))
View Solution
The energy difference between the two lines can be calculated using the formula: \[ \Delta E = \frac{h c \Delta \lambda}{\lambda^2}. \]
Substitute the given values: \[ \Delta E = \frac{4.125 \times 10^{-15} \times 3 \times 10^8 \times 0.14 \times 10^{-10}}{(6521 \times 10^{-10})^2}. \]
This gives: \[ \Delta E \approx 3 \times 10^{-5} \, eV. \]
Thus, the value of \( m \) is 3. Quick Tip: To calculate the energy difference between two spectral lines due to spin-orbit effects, use the formula \( \Delta E = \frac{h c \Delta \lambda}{\lambda^2} \).
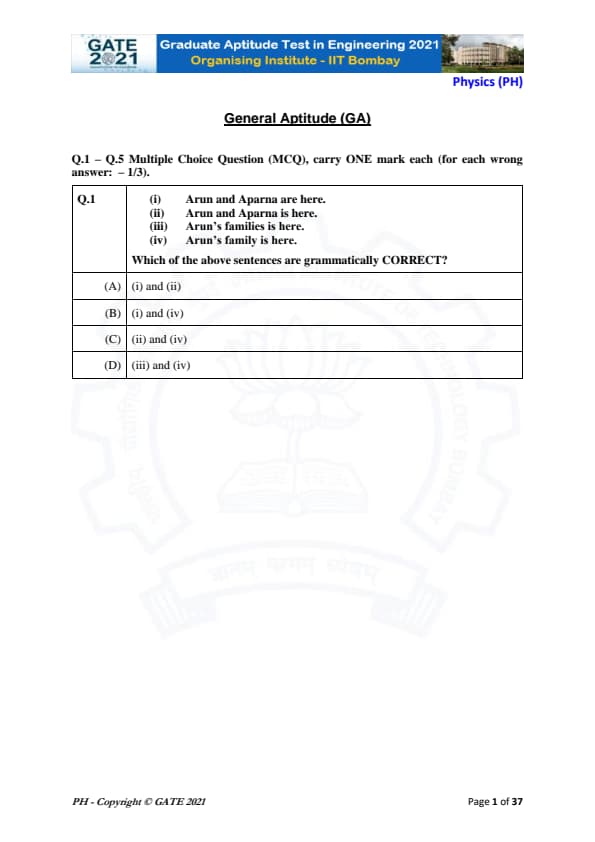





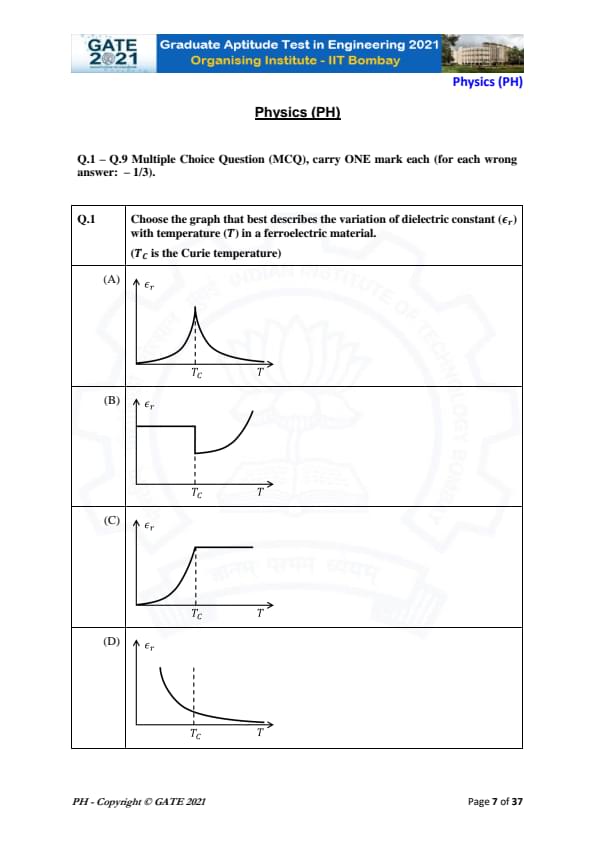

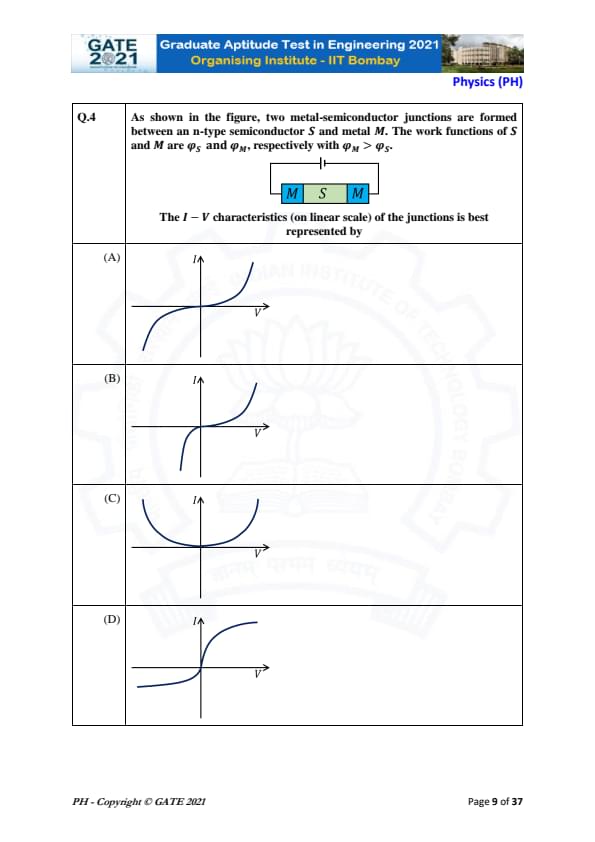
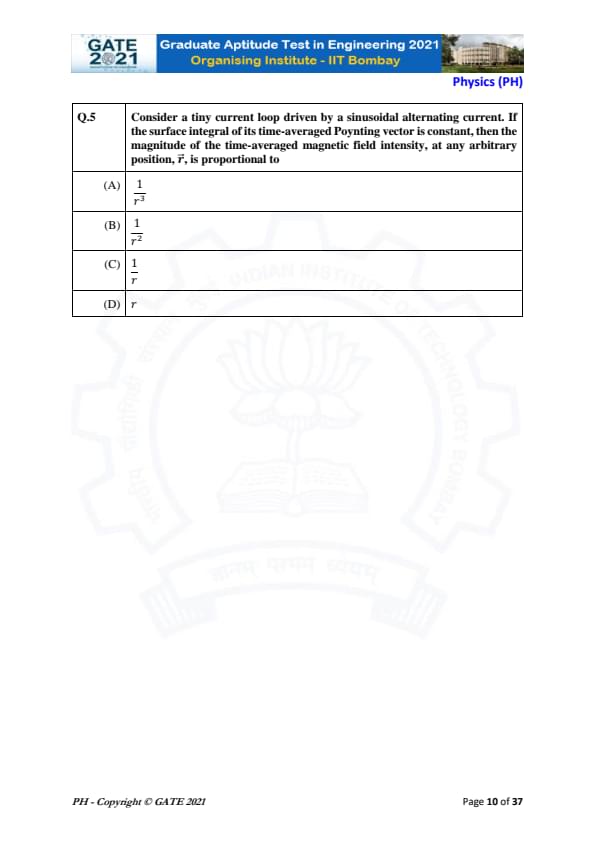
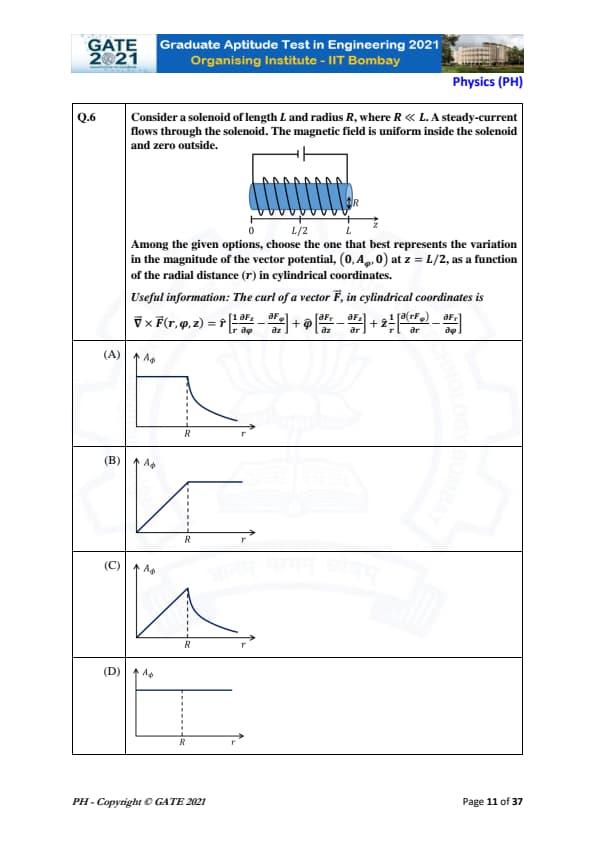


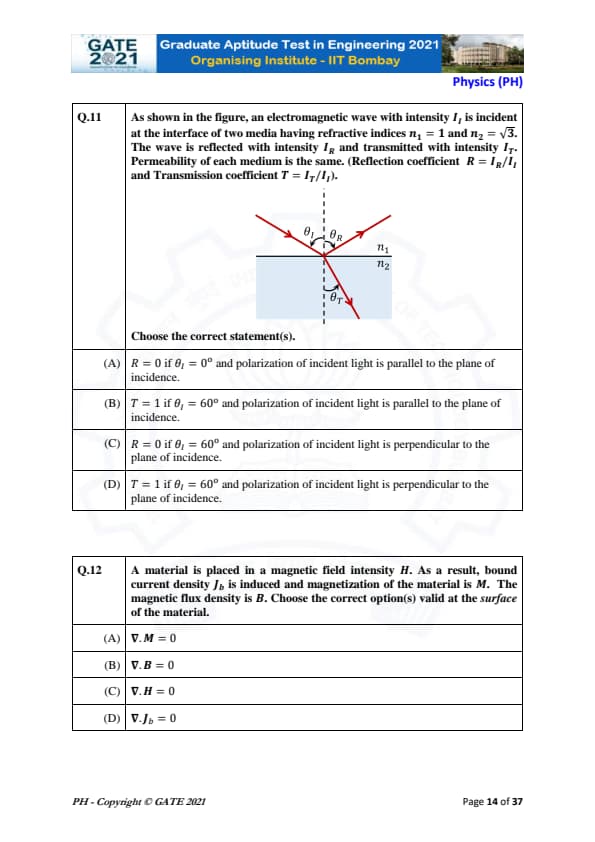

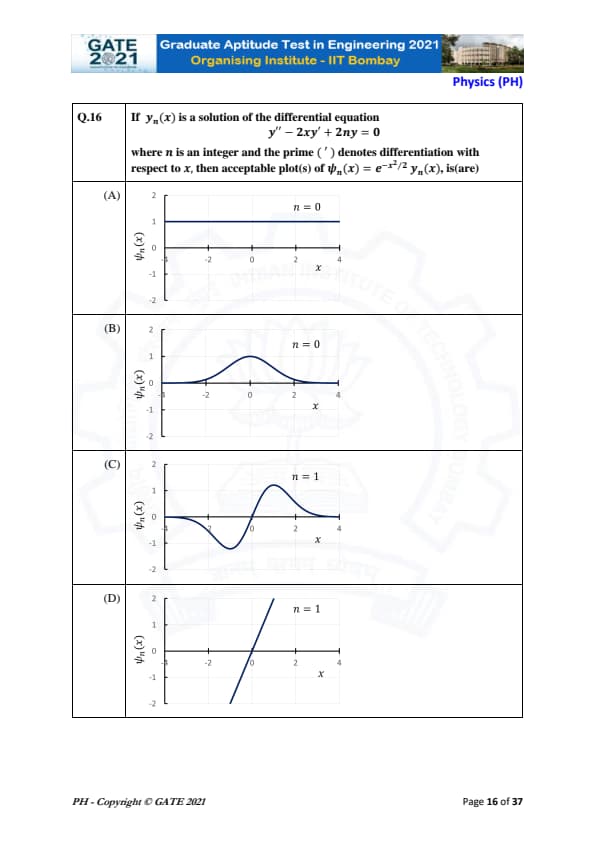










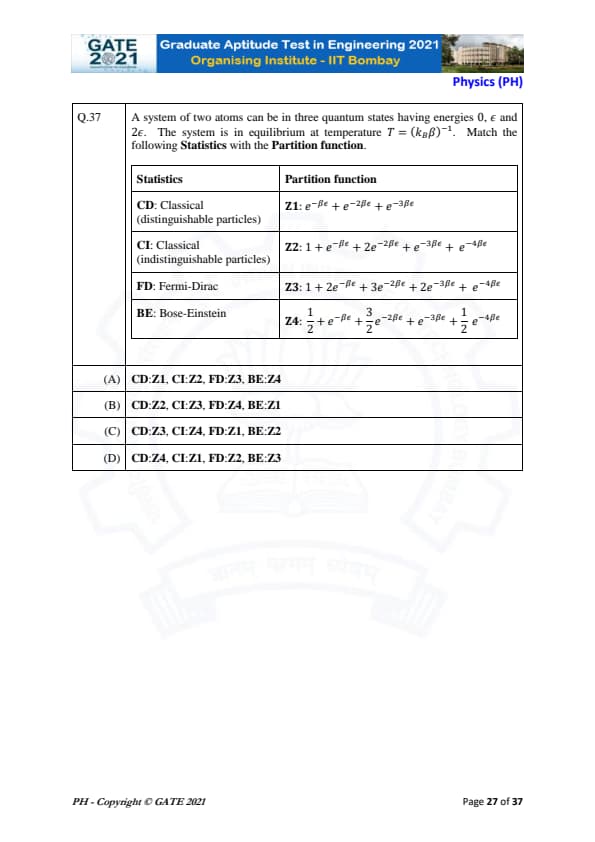
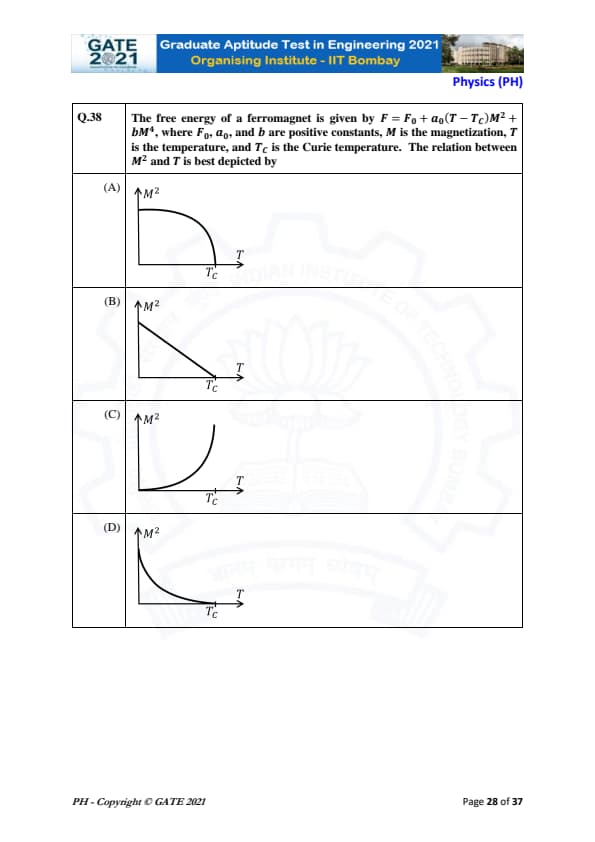
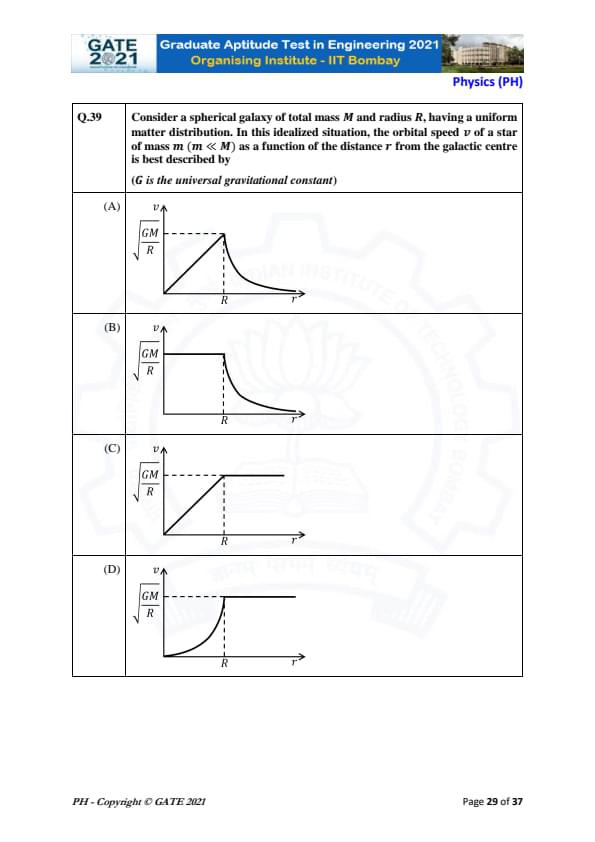
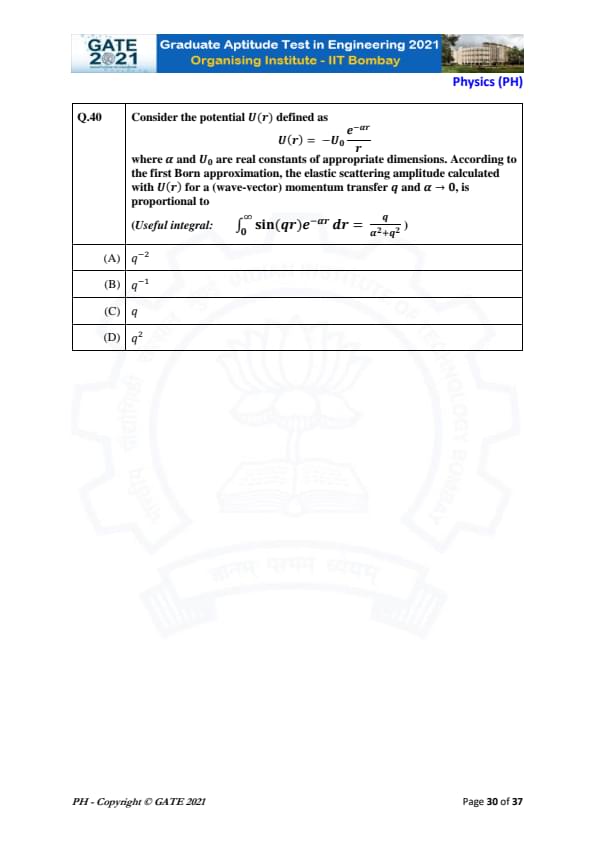







Cut Off for GATE Physics (PH) 2021
The subject-by-subject cut-off is also provided together with the result. The cut-off is the minimum qualifying score that candidates must achieve in order to be admitted to their desired course and college. GATE 2021 cut-off is determined by a number of factors, including the total number of candidates who took the exam, the difficulty level of the exam, the applicant category, and so on.
GATE Physics (PH) cut-off from the previous year 2020 is summarised as below;
| Paper | General | OBC (NCL) | SC / ST / PwD |
|---|---|---|---|
| Physics – PH | 37.2 | 33.4 | 24.8 |
Quick Links:
GATE 2021 PH Paper Analysis
- Overall difficulty level of GATE PH 2021 paper was moderate to difficult.
- General aptitude questions were easy to solve
- Good score was expected to be 65 and above.
- Numerical Type does not have any negative markings. However, every incorrect response will result in a 1/3rd negative marking for 1 marks and 2/3rd negative marking for 2 mark MCQ questions.
- Paper consists of 65 questions containing 100 maximum marks
Also Check:
GATE Previous Year Question Papers:
| GATE 2022 Question Papers | GATE 2021 Question Papers | GATE 2020 Question Papers |
| GATE 2019 Question Papers | GATE 2018 Question Papers | GATE 2017 Question Papers |





Comments