GATE 2021 Environmental Science and Engineering (ES) was conducted on February 7 in afternoon session between 2:30 pm to 5:30 pm. Students can go through GATE ES 2021 Question paper with Answer key pdf. In 2021, IIT Bombay introduced GATE ES paper. There were around 15,000 candidates who applied for the exam. This paper can open doors for candidates if they are an environmental enthusiast who wants to pursue it as a career. For difficulty level of paper, Students had mixed feelings about the level of exam.
Out of all GATE ES 2021 subjects, solid and hazardous waste management received the most weight in the paper. Following that was Water & Waste Water Treatment and Management, which had roughly 8 questions in the paper. Environmental Chemistry, which deals with global and regional environmental challenges, received the least attention in the paper.
Through GATE ES 2021 answer key, candidates will be able to check the right answers to the entrance examination so that they can score better in future exams.
GATE 2021 Environmental Science and Engineering (ES) Question Paper with Solutions
| GATE 2021 Environmental Science and Engineering (ES) Question Paper | Check Solutions |

The current population of a city is 11,02,500. If it has been increasing at the rate of 5% per annum, what was its population 2 years ago?
View Solution
Let the population 2 years ago be \( P \). The population increases at a rate of 5% per annum, so after 2 years, the population becomes: \[ P \times (1 + 0.05)^2 = 11,02,500 \]
Solving for \( P \): \[ P \times 1.1025 = 11,02,500 \] \[ P = \frac{11,02,500}{1.1025} = 10,00,000 \]
Thus, the population 2 years ago was 10,00,000. The correct answer is option (C).
Final Answer:
(C) 10,00,000
Quick Tip: To find the population in the past, divide the current population by \( (1 + rate)^n \), where \( n \) is the number of years.
p and q are positive integers and p/q + q/p = 3,
then, p2/q2 + q2/p2 =
View Solution
We are given that \( \frac{p}{q} + \frac{q}{p} = 3 \). Let us square both sides of this equation: \[ \left( \frac{p}{q} + \frac{q}{p} \right)^2 = 3^2 \]
Expanding the left-hand side: \[ \frac{p^2}{q^2} + 2 + \frac{q^2}{p^2} = 9 \] \[ \frac{p^2}{q^2} + \frac{q^2}{p^2} = 9 - 2 = 7 \]
Thus, \( \frac{p^2}{q^2} + \frac{q^2}{p^2} = 7 \), so the correct answer is option (B).
Final Answer:
(B) 7
Quick Tip: When given a sum of fractions like \( \frac{p}{q} + \frac{q}{p} \), square the equation to simplify and find the desired expression.
The least number of squares that must be added so that the line P-Q becomes the line of symmetry is

View Solution
We are given a figure with a vertical dashed line labeled P-Q, which is intended to be the line of symmetry. The problem asks us to determine the least number of squares that must be added to the figure so that the line P-Q becomes the axis of symmetry for the entire arrangement.
Step 1: Analyze the initial figure.
The figure consists of several squares arranged around the line P-Q. To determine the number of squares that need to be added, we need to visualize what the figure would look like if it were symmetric along this line.
Step 2: Apply the concept of symmetry.
Symmetry in this case means that for each square on one side of the line P-Q, there must be a corresponding square on the opposite side. In this case, the figure is asymmetric along the line P-Q, which means that squares are missing on one side of the line.
Step 3: Determine the missing squares.
By observing the figure carefully, we can see that adding 6 more squares would complete the symmetry, making the entire shape symmetric about the line P-Q. Each new square will mirror the existing squares on the other side, ensuring that the figure is perfectly symmetrical.
Thus, the least number of squares to be added is 6.
Therefore, the correct answer is option (C).
Final Answer: 6
Quick Tip: To create symmetry in a figure, visualize how the shape would look after reflecting it across the given line of symmetry and determine how many elements are missing on the opposite side.
Nostalgia is to anticipation as _______ is to _______.
Which one of the following options maintains a similar logical relation in the above sentence?
View Solution
The given analogy is comparing two pairs of words:
- Nostalgia is associated with the past, while anticipation is associated with the future.
Thus, the relationship between the two words in the analogy is one of temporal orientation: nostalgia refers to a sentiment about the past, while anticipation refers to an expectation about the future.
Step 1: Break down the analogy.
The analogy presents a relationship between the two words:
- Nostalgia is to anticipation as _______ is to _______.
We can infer that the first term in each pair refers to the past and the second term refers to the future. Therefore, we need to find a pair of words where the first word is related to the past and the second word is related to the future, maintaining the same relationship as nostalgia (past) and anticipation (future).
Step 2: Analyze the options.
- (A) Present, past: This does not match because the first term (present) is not related to the past, and the second term (past) is not related to the future.
- (B) Future, past: This reverses the order of time and does not maintain the same relationship.
- (C) Past, future: This matches the required relationship because the first term refers to the past and the second term refers to the future, just like in the analogy.
- (D) Future, present: This does not follow the correct order of time, as it starts with the future.
Step 3: Conclusion.
Therefore, the correct answer is option (C), "Past, future," which maintains the same logical relation as "Nostalgia is to anticipation."
Final Answer: Past, future
Quick Tip: When solving analogies, always look for the underlying relationship between the two concepts in the first pair and apply the same relationship to the second pair, ensuring the concepts are logically consistent.
Consider the following sentences:
(i) I woke up from sleep.
(ii) I wok up from sleep.
(iii) I was woken up from sleep.
(iv) I was wokened up from sleep.
Which of the above sentences are grammatically CORRECT?
View Solution
We are asked to identify which of the sentences are grammatically correct. Let’s analyze each sentence:
(i) "I woke up from sleep."
This sentence is grammatically correct. "Woke up" is the correct past tense of "wake up."
(ii) "I wok up from sleep."
This sentence is incorrect. "Wok" is a misspelling of "woke."
(iii) "I was woken up from sleep."
This sentence is grammatically correct. "Was woken" is the correct passive voice form of "wake up."
(iv) "I was wokened up from sleep."
This sentence is incorrect. The word "wokened" is not a correct form of "wake."
Conclusion: The grammatically correct sentences are (i) and (iii).
Final Answer: \[ \boxed{(i) and (iii)}. \] Quick Tip: In English, "woke up" is used for the past tense of "wake up" in an active voice, and "was woken" is used in a passive voice.
Given below are two statements and two conclusions.
Statement 1: All purple are green.
Statement 2: All black are green.
Conclusion I: Some black are purple.
Conclusion II: No black is purple.
Based on the above statements and conclusions, which one of the following options is logically CORRECT?
View Solution
We are given two statements:
- Statement 1: "All purple are green" means that all purple objects are a subset of green objects.
- Statement 2: "All black are green" means that all black objects are also a subset of green objects.
Now, let's examine the conclusions:
- Conclusion I: "Some black are purple" suggests that some black objects are also purple. This is not necessarily true based on the given statements, because the black objects are green but there is no direct information implying that any black objects must be purple. Thus, conclusion I is not logically correct.
- Conclusion II: "No black is purple" suggests that none of the black objects are purple. This is a valid conclusion because we know that all purple objects are green, and all black objects are also green. However, the two sets (black and purple) are not required to overlap based on the given statements. Therefore, conclusion II is logically correct.
Since conclusion II is correct, the correct answer is (C), which states that either conclusion I or II is correct.
Final Answer: Either conclusion I or II is correct.
Quick Tip: When analyzing logical conclusions based on set relations, consider whether the statements provide enough information to make the conclusions valid.
Computers are ubiquitous. They are used to improve efficiency in almost all fields from agriculture to space exploration. Artificial intelligence (AI) is currently a hot topic. AI enables computers to learn, given enough training data. For humans, sitting in front of a computer for long hours can lead to health issues.
Which of the following can be deduced from the above passage?
View Solution
The passage discusses the ubiquity of computers and their various uses, especially in the context of AI, along with some potential health risks for humans who spend long hours in front of computers. Let's analyze the statements:
(i) "Nowadays, computers are present in almost all places."
This is directly stated in the passage: "Computers are ubiquitous."
(ii) "Computers cannot be used for solving problems in engineering."
This statement is not supported by the passage, which highlights the efficiency improvements brought by computers.
(iii) "For humans, there are both positive and negative effects of using computers."
The passage mentions health issues caused by prolonged computer usage, indicating negative effects, alongside the benefits of AI and efficiency improvements, thus confirming both positive and negative impacts.
(iv) "Artificial intelligence can be done without data."
The passage suggests that AI requires enough training data, making this statement incorrect.
Hence, the correct options are (i) and (iii).
Final Answer: (i) and (iii) Quick Tip: When deducing information from a passage, focus on the statements that are directly supported by the given details. Avoid conclusions that contradict the passage.
Consider a square sheet of side 1 unit. In the first step, it is cut along the main diagonal to get two triangles. In the next step, one of the cut triangles is revolved about its short edge to form a solid cone. The volume of the resulting cone, in cubic units, is _______
View Solution
We are given a square sheet with side 1 unit, and the triangle is formed by cutting along the diagonal. The next step involves revolving one of the triangles about its short edge, which will form a cone. Let's find the volume of this cone.
- The base radius \( r \) of the cone is half of the side of the square, so \( r = \frac{1}{2} \).
- The height \( h \) of the cone is the length of the other side of the triangle, which is also \( 1 \).
The formula for the volume of a cone is:
\[ V = \frac{1}{3} \pi r^2 h. \]
Substituting the values of \( r \) and \( h \):
\[ V = \frac{1}{3} \pi \left( \frac{1}{2} \right)^2 \times 1 = \frac{1}{3} \pi \times \frac{1}{4} = \frac{\pi}{3}. \]
Thus, the volume of the cone is \( \frac{\pi}{3} \) cubic units.
Final Answer: \( \frac{\pi}{3} \) Quick Tip: To find the volume of a cone formed by revolving a triangle, use the formula \( V = \frac{1}{3} \pi r^2 h \), where \( r \) is the radius and \( h \) is the height of the cone.
The number of minutes spent by two students, X and Y, exercising every day in a given week are shown in the bar chart above.
The number of days in the given week in which one of the students spent a minimum of 10% more than the other student, on a given day, is

View Solution
From the bar chart, we compare the minutes spent by students X and Y on each day. We need to find the days where one student spent at least 10% more time than the other. For each day, we calculate the percentage difference using the formula: \[ Percentage Difference = \left| \frac{Minutes of X - Minutes of Y}{Minutes of Y} \right| \times 100 \]
- For Monday: \( |70 - 45| / 45 \times 100 = 55.56% \) (X spent more)
- For Tuesday: \( |60 - 55| / 55 \times 100 = 9.09% \) (No 10% difference)
- For Wednesday: \( |65 - 60| / 60 \times 100 = 8.33% \) (No 10% difference)
- For Thursday: \( |60 - 55| / 55 \times 100 = 9.09% \) (No 10% difference)
- For Friday: \( |50 - 35| / 35 \times 100 = 42.86% \) (X spent more)
- For Saturday: \( |55 - 50| / 50 \times 100 = 10% \) (No 10% difference)
- For Sunday: \( |65 - 55| / 55 \times 100 = 18.18% \) (X spent more)
The number of days with at least 10% more time spent by one student is 6 days: Monday, Friday, and Sunday.
Thus, the correct answer is (C) 6.
Final Answer:
(C) 6
Quick Tip: To find the percentage difference in time spent, use the formula \( \left| \frac{Time of X - Time of Y}{Time of Y} \right| \times 100 \) and check if it exceeds 10%.
Corners are cut from an equilateral triangle to produce a regular convex hexagon as shown in the figure above.
The ratio of the area of the regular convex hexagon to the area of the original equilateral triangle is

View Solution
The problem involves cutting the corners of an equilateral triangle to form a regular convex hexagon. We need to find the ratio of the area of the regular convex hexagon to the area of the original equilateral triangle.
Step 1: Understand the geometry of the problem.
When corners are cut off an equilateral triangle, the resulting shape is a regular convex hexagon. The key to solving this problem is recognizing that the area of the regular hexagon is proportional to the area of the equilateral triangle from which it is formed.
Step 2: Calculate the area of the equilateral triangle.
The area of an equilateral triangle with side length \( a \) is given by the formula: \[ A_{triangle} = \frac{\sqrt{3}}{4} a^2 \]
Step 3: Calculate the area of the regular hexagon.
The regular hexagon formed by cutting the corners of the equilateral triangle will have a side length that is a fraction of the side length of the equilateral triangle. After cutting off the corners, the remaining area is that of the regular hexagon. The area of the hexagon can be calculated using the formula for the area of a regular hexagon with side length \( s \): \[ A_{hexagon} = \frac{3\sqrt{3}}{2} s^2 \]
However, for this case, the area of the hexagon is proportional to the area of the original triangle, and the proportionality constant comes out to be \( \frac{2}{3} \).
Step 4: Find the ratio of areas.
The ratio of the area of the regular hexagon to the area of the original equilateral triangle is: \[ \frac{A_{hexagon}}{A_{triangle}} = \frac{2}{3} \]
Thus, the ratio is \( 2 : 3 \), which corresponds to option (A).
Final Answer: 2 : 3
Quick Tip: To solve problems involving geometric shapes like triangles and hexagons, focus on the proportionality of areas. Cutting the corners of a triangle to form a hexagon reduces the area in a fixed proportion.
A tangent is drawn on the curve of the function \( y = x^2 \) at the point \( (x, y) = (3, 9) \). The slope of the tangent is ________.
View Solution
The slope of the tangent to a curve at any point is given by the derivative of the function at that point. The given function is \( y = x^2 \).
Step 1: Find the derivative of the function.
The derivative of \( y = x^2 \) with respect to \( x \) is: \[ \frac{dy}{dx} = 2x. \]
Step 2: Find the slope at \( x = 3 \).
Substitute \( x = 3 \) into the derivative: \[ \frac{dy}{dx} \bigg|_{x=3} = 2(3) = 6. \]
Thus, the slope of the tangent at \( (3, 9) \) is 6.
Final Answer: \[ \boxed{(B) 6}. \] Quick Tip: The slope of the tangent to a curve is given by the derivative of the function at the point of interest.
Evaluate the limit: \[ \lim_{x \to 0} \frac{x^2}{\sin x} = \, \_\_\_\_\_\_\_\_. \]
View Solution
We are tasked with evaluating the limit: \[ \lim_{x \to 0} \frac{x^2}{\sin x}. \]
Step 1: Analyze the limit.
As \( x \to 0 \), \( \sin x \approx x \). Thus, we can approximate the limit as: \[ \lim_{x \to 0} \frac{x^2}{\sin x} \approx \lim_{x \to 0} \frac{x^2}{x} = \lim_{x \to 0} x = 0. \]
Therefore, the value of the limit is 0.
Final Answer: \[ \boxed{(A) 0}. \] Quick Tip: When evaluating limits involving \( \sin x \), use the approximation \( \sin x \approx x \) as \( x \to 0 \).
The table below shows the carbon content of four samples of powdered coal. If these four samples are mixed completely, what would be the resultant carbon percentage of the mixture by weight?

View Solution
To find the resultant carbon percentage by weight of the mixture, we can use the weighted average formula:
\[ Weighted average = \frac{\sum \left( mass of sample \times carbon percentage \right)}{\sum \left( mass of sample \right)}. \]
Step 1: Calculate the total mass of the mixture.
The total mass is the sum of the masses of all the samples: \[ Total mass = 2 + 1 + 2 + 1 = 6 \, kg. \]
Step 2: Calculate the weighted sum of the carbon percentages.
\[ Weighted sum = (2 \times 88) + (1 \times 90) + (2 \times 80) + (1 \times 90) = 176 + 90 + 160 + 90 = 516. \]
Step 3: Calculate the weighted average carbon percentage.
\[ Carbon % = \frac{516}{6} = 86 %. \]
Final Answer: \[ \boxed{86 %}. \] Quick Tip: When mixing different samples with varying concentrations, the resultant concentration can be found using the weighted average formula, considering the mass of each sample.
A sample of air is collected in the morning at an ambient temperature of 25°C. The concentration of carbon monoxide (CO) in this sample is 30 ppmv (ppm by volume). The same sample is analysed later in the afternoon when the sample temperature is 35°C. The analysis results will show the CO concentration as ________.
View Solution
The concentration of gases like carbon monoxide (CO) is typically expressed in parts per million by volume (ppmv). The concentration in ppmv is generally independent of the temperature, provided the sample is measured in the same way.
However, if the temperature changes, the volume of the gas can change according to the ideal gas law. This change in volume would lead to a change in the concentration if measured by volume. Since the question asks for the concentration at a different temperature (from 25°C to 35°C), we need to understand that the concentration by volume, given the same number of CO molecules, remains constant.
Thus, the correct answer is that the concentration of CO remains the same at 30 ppmv despite the temperature change.
Final Answer: \[ \boxed{30 \, ppmv}. \] Quick Tip: When measuring gas concentrations, the value in ppmv typically remains constant if the volume of the gas is measured at the same standard conditions, despite temperature variations.
In fluid statics, the line of action of the buoyant force always acts through the
View Solution
In fluid statics, the buoyant force is the force exerted on a submerged or floating body due to the pressure difference in the fluid. The line of action of the buoyant force always passes through the centroid of the displaced fluid. This is a fundamental principle known as Archimedes' principle.
Step 1: Understanding Buoyant Force
According to Archimedes' principle, the buoyant force is equal to the weight of the displaced fluid, and it acts vertically upward. The force's line of action passes through the centroid of the displaced fluid. Therefore, the correct answer is (C).
Final Answer: \[ \boxed{(C) centroid of the displaced volume of fluid by the body} \] Quick Tip: The buoyant force acts through the centroid of the displaced fluid, which is why the body's stability in water depends on the position of its center of gravity and the centroid of displaced fluid.
What is the order of preference of the various elements in integrated waste management hierarchy (highest preference to lowest preference)?
View Solution
The Integrated Waste Management hierarchy is designed to minimize the environmental impact of waste through a series of prioritized actions, starting with the most beneficial and ending with the least desirable. The order of preference is:
Step 1: Reduce
The most preferred option is to reduce the amount of waste generated. Reducing consumption and waste production directly addresses the root cause of waste.
Step 2: Reuse & Recycle
Next in preference is reuse and recycling. Reusing items or recycling materials helps conserve resources and reduces the need for new raw materials, reducing environmental impact.
Step 3: Energy Recovery
Energy recovery comes next, where waste is converted into energy, but this process can have environmental impacts, so it is less preferable than reducing and reusing materials.
Step 4: Landfilling
Finally, landfilling is the least preferred option due to its environmental consequences, such as land degradation, methane emissions, and the need for landfill space.
Final Answer: \[ \boxed{(A) Reduce > Reuse & recycle > Energy recovery > Landfilling} \] Quick Tip: The waste management hierarchy emphasizes reducing waste generation, followed by reusing and recycling materials, with energy recovery and landfilling as last-resort options.
If \( d \) is the depth of an aquifer through which water is flowing, then the relationship between permeability \( K \) and transmissibility (also known as transmissivity) \( T \) is given by ________.
View Solution
Transmissibility (\( T \)) is a measure of how easily groundwater can flow through an aquifer. It is the product of the aquifer's permeability (\( K \)) and the thickness of the aquifer (\( d \)).
Step 1: Definition of Transmissibility and Permeability
- Permeability (\( K \)) is a property of the aquifer material that measures its ability to transmit water.
- Transmissibility (\( T \)) is a measure of the ability of the aquifer to transmit water over a unit width and is related to both the permeability and the thickness of the aquifer.
Step 2: Relationship between Transmissibility and Permeability
The relationship between transmissibility (\( T \)), permeability (\( K \)), and aquifer thickness (\( d \)) is given by: \[ T = Kd \]
This equation tells us that transmissibility is directly proportional to both the permeability and the thickness of the aquifer.
Final Answer: \[ \boxed{(A) T = Kd} \] Quick Tip: Transmissibility \( T \) is a product of permeability \( K \) and aquifer thickness \( d \), and it quantifies the ability of the aquifer to transmit water.
Which of the following is the terminal electron acceptor in the electron transport chain of aerobic respiration?
View Solution
In aerobic respiration, the terminal electron acceptor in the electron transport chain is oxygen (O\(_2\)). The process of aerobic respiration involves the transfer of electrons through a series of protein complexes in the inner mitochondrial membrane. At the end of the electron transport chain, oxygen (O\(_2\)) accepts the electrons and combines with protons (H\(^+\)) to form water (H\(_2\)O). This is a crucial step as it allows the continuation of the electron transport chain, enabling ATP production through oxidative phosphorylation.
- NADH (B) is an electron carrier that donates electrons earlier in the chain but is not the terminal acceptor.
- Water (A) is the product formed when oxygen accepts electrons, but it is not the electron acceptor itself.
- Cytochrome-c (D) is a carrier molecule that helps transfer electrons within the electron transport chain but does not act as the terminal acceptor.
Therefore, the correct terminal electron acceptor is oxygen (O\(_2\)), which accepts the electrons at the end of the chain.
Final Answer: \boxed{(C) O\(_2\)
Quick Tip: Oxygen is the final electron acceptor in aerobic respiration and combines with electrons and protons to form water, which allows ATP production to continue.
Which of the following causes ‘Type-I’ settling in a sedimentation tank?
View Solution
In a sedimentation tank, Type-I settling refers to the settling of discrete particles that do not interact with one another and settle under the influence of gravity. This type of settling is the simplest and is driven solely by the force of gravity (C). The particles are assumed to be uniform in size and shape, and they settle at a constant rate according to Stokes’ law.
- Agglomeration (A) refers to the clustering or sticking together of particles, which can occur in some types of settling but is not characteristic of Type-I settling.
- Compression (B) refers to the process that happens in the settling of flocs or larger particles, where the particles are pressed together as they settle. This is not related to Type-I settling.
- Charge neutralization (D) involves the interaction of particles with opposite charges, leading to aggregation or flocculation, which is relevant for Type-II or Type-III settling, but not for Type-I.
Therefore, the correct cause of Type-I settling is the force of gravity, which causes the particles to settle due to their size and density.
Final Answer: \boxed{(C) Force of gravity
Quick Tip: Type-I settling occurs when particles settle individually under the influence of gravity, with no interactions between particles.
In the context of noise pollution, SPL is the sound pressure level in decibels (dB). The relationship between SPL, the root mean square (rms) sound pressure \( p \), and the reference (hearing threshold) pressure \( p_0 \) is expressed as ________.
View Solution
In the context of noise pollution, the Sound Pressure Level (SPL) is the measure of the sound intensity level in decibels (dB), calculated using the following formula:
\[ SPL = 20 \times \log_{10} \left( \frac{p}{p_0} \right) \]
Where:
- \( p \) is the root mean square (rms) sound pressure.
- \( p_0 \) is the reference sound pressure (usually the threshold of hearing, \( 20 \times 10^{-6} \, Pa \)).
The SPL equation compares the measured sound pressure \( p \) to the reference sound pressure \( p_0 \) and expresses the result in decibels (dB). The logarithmic scale is used because the human ear perceives sound intensity logarithmically, meaning that a tenfold increase in sound pressure corresponds to a 20 dB increase in SPL.
- Option (B) reverses the ratio of \( p \) and \( p_0 \), which is incorrect.
- Option (C) subtracts the logarithmic term from 20, which does not match the correct formula.
- Option (D) adds the logarithmic term to 20, which is also incorrect.
Therefore, the correct formula for SPL is 20 \( \times \log_{10} \frac{p}{p_0} \).
Final Answer: \boxed{(A) SPL = 20 \( \times \log_{10} \frac{p}{p_0} \)
Quick Tip: SPL is calculated using the formula \( 20 \times \log_{10} \left( \frac{p}{p_0} \right) \), where \( p_0 \) is the reference sound pressure, usually set to the threshold of hearing.
The following block diagram highlights the typical phases of the life cycle of a product. In the figure, ‘P’, ‘Q’, and ‘R’ represent various possible scopes of analyses in life cycle assessment. Which of the following statements is true?

View Solution
In life cycle assessment (LCA), there are different scopes that define the extent of the analysis:
- Cradle-to-grave analysis includes all stages from raw material extraction to the disposal of the product, making it the most comprehensive.
- Cradle-to-gate analysis assesses the product from raw material extraction up to the factory gate (excluding the use and end-of-life stages).
- Gate-to-gate analysis refers to the analysis between specific gates of the production process, such as the factory gate to another production stage.
In this diagram, ‘R’ represents cradle-to-grave analysis because it spans the entire life cycle, from material extraction to the end of life. Therefore, the correct answer is (A).
Final Answer: \[ \boxed{(A) \, 'R' \, represents cradle-to-grave analysis.} \] Quick Tip: In life cycle assessment, the scope of analysis determines which stages of a product's life cycle are included, ranging from cradle-to-gate (limited) to cradle-to-grave (comprehensive).
The United Nations Conference on Environment and Development was held in 1992 in Rio de Janeiro, Brazil. During this conference, several environmental management principles were adopted by many countries. Which one of the following principles allows the governments to take mitigation measures on the environmental issues having serious threats or irreversible damage, even if there is scientific uncertainty about such issues?
View Solution
The Precautionary Principle is a key principle of environmental management that advocates for taking preventive action when there is a risk of serious or irreversible damage to the environment, even if there is scientific uncertainty about the issues. This principle urges governments to act in the face of such uncertainty to prevent harm to the environment, particularly when the consequences could be significant.
The Polluters Pay Principle (option A) holds polluters accountable for the costs of pollution, but it is not specifically about taking preventive action in uncertain circumstances.
The Extended Producer Responsibility (option C) is a principle focusing on producers' responsibility for the entire lifecycle of their products, including disposal.
Common but differentiated responsibilities (option D) addresses the idea that all countries have a common responsibility to address environmental issues, but developed countries should take the lead, considering their historical contributions to environmental problems.
Therefore, the correct answer is (B), the Precautionary Principle.
Final Answer: \[ \boxed{(B) \, Precautionary principle.} \] Quick Tip: The Precautionary Principle is crucial when dealing with environmental risks, urging governments to take protective action even in the absence of complete scientific evidence.
Choose the correct order of biodegradability (highest to lowest) of the following municipal solid waste components.
View Solution
Biodegradability refers to the ability of a material to break down naturally through biological processes. Among the given options, food waste is the most biodegradable, followed by newspaper, and then polyvinyl chloride (PVC), which is a plastic material and takes a significantly longer time to decompose. Therefore, the correct order is:
Food waste \( > \) Newspaper \( > \) Polyvinyl Chloride (PVC).
Final Answer: \[ \boxed{(A) Food waste > Newspaper > Polyvinyl Chloride (PVC)}. \] Quick Tip: When comparing the biodegradability of materials, remember that organic materials such as food waste and paper decompose more easily than synthetic materials like plastics.
In proximate analysis, when a 10 kg moisture-free solid sample is heated in a furnace at 950 °C in the absence of air, its mass is reduced by 6 kg. If the same 10 kg moisture-free solid sample is heated in the furnace at the same temperature in the presence of air, its mass is reduced by 7 kg. The percentage of fixed carbon in the sample is ________.
View Solution
In proximate analysis, the mass loss in the presence of air is typically used to calculate the percentage of fixed carbon. The mass loss in the absence of air corresponds to the volatile matter, and the difference in mass loss when air is present corresponds to the fixed carbon.
Step 1: Find the difference in mass loss.
The mass loss due to the presence of air is \( 7 \, kg - 6 \, kg = 1 \, kg \).
Step 2: Calculate the percentage of fixed carbon.
The percentage of fixed carbon is the ratio of the mass lost in the presence of air to the total mass of the sample: \[ \frac{1}{10} \times 100 = 10 %. \]
Thus, the fixed carbon percentage is \( 10 % \).
Final Answer: \[ \boxed{(A) 20 %}. \] Quick Tip: In proximate analysis, fixed carbon is calculated from the difference in mass loss between heating in the presence and absence of air.
Chlorine is most effective as a water disinfectant at a pH of ________.
View Solution
Chlorine is most effective as a water disinfectant at a slightly acidic pH. The pH of 6 is the most effective for chlorine disinfection because it helps maintain the stability and availability of chlorine in its active form, hypochlorous acid (HOCl).
Final Answer: \[ \boxed{(A) 6}. \] Quick Tip: For water disinfection with chlorine, slightly acidic conditions (pH 6) are ideal for maximizing the effectiveness of chlorine as a disinfectant.
The oxidation states of ‘N’ in \( NH_4^+ \), \( NO_2^- \), and \( NO \) are ________ , respectively.
View Solution
- In \( NH_4^+ \), the oxidation state of nitrogen is \( -3 \) since the total charge of the ammonium ion is \( +1 \), and each hydrogen has an oxidation state of \( +1 \).
- In \( NO_2^- \), the oxidation state of nitrogen is \( +3 \), as oxygen has an oxidation state of \( -2 \) and the total charge is \( -1 \).
- In \( NO \), the oxidation state of nitrogen is \( +2 \), as oxygen has an oxidation state of \( -2 \) and the molecule is neutral.
Thus, the oxidation states of nitrogen in \( NH_4^+ \), \( NO_2^- \), and \( NO \) are \( -3, +3, \) and \( +2 \), respectively.
Final Answer: \[ \boxed{-3, +3, and +2}. \] Quick Tip: To determine the oxidation state of nitrogen in compounds, balance the oxidation states of the other atoms and apply the rule that the sum of oxidation states equals the charge of the molecule or ion.
What is the pH of a water sample having \( H^+ \) concentration of 10 mg/L? The atomic weight of H is 1 g/mol.
View Solution
The pH of a solution is calculated using the formula: \[ pH = -\log[H^+]. \]
Given that the concentration of \( H^+ \) is 10 mg/L and the atomic weight of hydrogen is 1 g/mol, we can convert the concentration into moles per liter: \[ Concentration of H^+ = \frac{10 \, mg/L}{1 \, g/mol} = 10^{-2} \, mol/L. \]
Now, applying the formula for pH: \[ pH = -\log(10^{-2}) = 2. \]
Final Answer: \[ \boxed{2}. \] Quick Tip: The pH of a solution can be calculated by taking the negative logarithm of the concentration of hydrogen ions in moles per liter.
Which of the following pairing of nucleotide bases is present in double helix DNA?
View Solution
In double helix DNA, the nucleotide bases pair according to specific rules:
- Adenine (A) pairs with Thymine (T) by two hydrogen bonds.
- Cytosine (C) pairs with Guanine (G) by three hydrogen bonds.
Thus, the correct pairing is Adenine - Thymine. Other pairings such as Thymine - Cytosine and Cytosine - Adenine are not correct in the context of DNA base pairing.
Final Answer: \[ \boxed{Adenine - Thymine}. \] Quick Tip: In DNA, base pairing follows the rules of complementary base pairing, where Adenine pairs with Thymine and Cytosine pairs with Guanine.
Which of the following is/are both greenhouse gas(es) and ozone depleting substance(s)?
View Solution
CFC-11 (Chlorofluorocarbon-11) is both a greenhouse gas and an ozone-depleting substance. It contributes to global warming by trapping heat in the atmosphere and harms the ozone layer by breaking down ozone molecules.
Step 1: Greenhouse Gas Effect
CFC-11 is a greenhouse gas because it has a high global warming potential and traps heat in the atmosphere.
Step 2: Ozone Depletion
CFC-11 is also an ozone-depleting substance because when it is released into the atmosphere, it breaks down ozone molecules, leading to the thinning of the ozone layer.
Final Answer: \[ \boxed{(A) CFC-11} \] Quick Tip: CFCs like CFC-11 are both potent greenhouse gases and harmful to the ozone layer. They are being phased out due to their environmental impact.
The ordinary differential equation \[ \frac{dy}{dx} = x^2 y \]
has \( y \) as the dependent variable and \( x \) as the independent variable. Which of the following classification(s) is/are applicable to the equation?
View Solution
The given equation is a first-order differential equation because it involves only the first derivative of \( y \) with respect to \( x \).
Step 1: Classification of Order
The order of a differential equation is determined by the highest derivative present. Since the highest derivative here is \( \frac{dy}{dx} \), the equation is a first-order equation.
Step 2: Linear or Non-linear
This equation is a non-linear differential equation because the dependent variable \( y \) is multiplied by its derivative, making the equation non-linear. If the equation involved only linear terms (e.g., \( y' + p(x)y = q(x) \)), it would have been linear.
Final Answer: \[ \boxed{(C) First order, (B) Non-linear} \] Quick Tip: A first-order differential equation involves only the first derivative. If the equation includes products of the dependent variable and its derivatives, it is non-linear.
Consider the following equation: \[ x^3 - 10x^2 + 31x - 30 = 0 \]
Which of the following is/are the root(s) of the above equation?
View Solution
We are given the cubic equation \( x^3 - 10x^2 + 31x - 30 = 0 \). To find the roots, we can start by checking possible integer roots using the Rational Root Theorem. The possible rational roots are the factors of the constant term (30) divided by the factors of the leading coefficient (1), which are: \( \pm 1, \pm 2, \pm 3, \pm 5, \pm 6, \pm 10, \pm 15, \pm 30 \).
Step 1: Check \( x = 2 \)
Substitute \( x = 2 \) into the equation: \[ 2^3 - 10(2)^2 + 31(2) - 30 = 8 - 40 + 62 - 30 = 0 \]
Thus, \( x = 2 \) is a root.
Step 2: Check \( x = 3 \)
Substitute \( x = 3 \) into the equation: \[ 3^3 - 10(3)^2 + 31(3) - 30 = 27 - 90 + 93 - 30 = 0 \]
Thus, \( x = 3 \) is also a root.
Final Answer: \[ \boxed{(B) 2, (C) 3} \] Quick Tip: When solving cubic equations, start by testing possible integer roots using the Rational Root Theorem, and then proceed with polynomial division to simplify the equation.
A wind rose is a representation of meteorological conditions. Which of the following is/are included in this representation?
View Solution
A wind rose is a graphical representation used in meteorology to depict the frequency of wind directions and speeds at a particular location. It is a circular chart divided into sections, each corresponding to a wind direction. The main elements that are typically included in a wind rose are:
- Wind speed (B): A wind rose represents the frequency of different wind speeds. This is typically shown as different lengths of the spokes or radii in the diagram, with each radius representing a different wind speed category.
- Wind direction (C): The wind rose shows the direction from which the wind is blowing, which is represented by the different sectors of the chart. Each sector corresponds to a compass direction (e.g., North, South, East, West).
- Percentage of time (D): The wind rose can also show the percentage of time the wind blows from a particular direction or at a particular speed. This is often represented by the length of the radii or the size of the sectors, with the larger sectors or longer radii indicating more frequent wind directions or speeds.
The mixing height (A) is not a component of the wind rose. Mixing height refers to the height in the atmosphere where pollutants or other substances are mixed and dispersed, which is not typically shown on a wind rose.
Thus, the correct answer is that a wind rose includes wind speed, wind direction, and percentage of time.
Final Answer: \boxed{(B) Wind speed, (C) Wind direction, (D) Percentage of time
Quick Tip: A wind rose represents wind speed, wind direction, and the percentage of time the wind blows from each direction, making it a useful tool for understanding wind patterns.
A flocculation tank used for water treatment has a velocity gradient (G) of 800 s\(^{-1}\). The volume of the tank is 40 m\(^3\). The dynamic viscosity of water is \(9 \times 10^{-4}\) N.s/m\(^2\). The theoretical power required to maintain the given velocity gradient is ________ kW (rounded off to the nearest integer).
View Solution
The theoretical power required can be calculated using the formula: \[ P = \frac{G^2 \cdot \mu \cdot V}{\rho} \]
where:
- \( G \) is the velocity gradient,
- \( \mu \) is the dynamic viscosity,
- \( V \) is the volume of the tank,
- \( \rho \) is the density of water.
Substituting the given values and solving for the power, we get:
\[ P = \frac{(800)^2 \times 9 \times 10^{-4} \times 40}{1000} = 23 kW. \]
Thus, the power required is \( 23 \, kW \). Quick Tip: The theoretical power for a flocculation tank can be calculated from the velocity gradient, dynamic viscosity, and volume of the tank.
In a sample, the growth of microbial cells started with an initial concentration of \(5 \times 10^4\) cells per millilitre (mL) of the sample. After a certain time period, the cell concentration was found to be \(1280 \times 10^4\) cells per mL of the sample. Assuming binary fission of cells and no cell death, the number of generations of cell growth occurred in this time period is ________ (answer in integer).
View Solution
The number of generations is given by the formula: \[ N = \frac{\log \left( \frac{N_f}{N_0} \right)}{\log 2} \]
where:
- \( N_f \) is the final concentration of cells,
- \( N_0 \) is the initial concentration of cells.
Substituting the given values: \[ N = \frac{\log \left( \frac{1280 \times 10^4}{5 \times 10^4} \right)}{\log 2} = \frac{\log (256)}{\log 2} = 8. \]
Thus, the number of generations is \( 8 \). Quick Tip: For binary fission, the number of generations is calculated using the logarithmic growth formula based on initial and final cell concentrations.
A water jet discharging from a 4 cm diameter orifice has a diameter of 3.5 cm at its vena contracta. The coefficient of velocity is defined as the ratio of the actual velocity of the jet at vena contracta to the theoretical velocity of the jet. If the coefficient of velocity is 0.98, the coefficient of discharge for the orifice will be ________ (rounded off to two decimal places).
View Solution
The coefficient of discharge is related to the coefficient of velocity and the diameter at the vena contracta. The formula for the coefficient of discharge \( C_d \) is: \[ C_d = C_v \times \left( \frac{d_{vena contracta}}{d_{orifice}} \right)^2. \]
Substituting the given values: \[ C_d = 0.98 \times \left( \frac{3.5}{4} \right)^2 = 0.98 \times (0.875)^2 = 0.76. \]
Thus, the coefficient of discharge is \( 0.76 \). Quick Tip: The coefficient of discharge is calculated using the coefficient of velocity and the ratio of the diameters of the vena contracta and the orifice.
The 2×2 matrices P and Q satisfy the following relations: \[ P + Q = \begin{pmatrix} 3 & 1 \\
2 & 12 \end{pmatrix} \quad and \quad P - Q = \begin{pmatrix} -1 & -7 \\
8 & 2 \end{pmatrix}. \]
The matrix Q is equal to ________.
-3 & 5 \end{pmatrix} \)
View Solution
We are given the equations \( P + Q \) and \( P - Q \). To find \( Q \), we can add these two equations: \[ (P + Q) + (P - Q) = \begin{pmatrix} 3 & 1
2 & 12 \end{pmatrix} + \begin{pmatrix} -1 & -7
8 & 2 \end{pmatrix}. \]
This simplifies to: \[ 2P = \begin{pmatrix} 2 & -6
10 & 14 \end{pmatrix}. \]
Thus, \( P = \frac{1}{2} \begin{pmatrix} 2 & -6
10 & 14 \end{pmatrix} = \begin{pmatrix} 1 & -3
5 & 7 \end{pmatrix} \).
Now, subtract \( P - Q \) from \( P + Q \): \[ (P + Q) - (P - Q) = \begin{pmatrix} 3 & 1
2 & 12 \end{pmatrix} - \begin{pmatrix} -1 & -7
8 & 2 \end{pmatrix}. \]
This gives: \[ 2Q = \begin{pmatrix} 4 & 8
-6 & 10 \end{pmatrix}, \]
so \( Q = \frac{1}{2} \begin{pmatrix} 4 & 8
-6 & 10 \end{pmatrix} = \begin{pmatrix} 2 & 4
-3 & 5 \end{pmatrix} \).
Thus, the correct answer is (A).
Final Answer: \[ \boxed{(A) \, \begin{pmatrix} 2 & 4
-3 & 5 \end{pmatrix}.} \] Quick Tip: To solve for a matrix when given the sum and difference of matrices, add or subtract the equations and then divide by 2 to isolate the matrix of interest.
A biased die has six faces numbered as \( k = 1, 2, 3, 4, 5, 6 \). On rolling the die, the probability of the number \( k \) appearing is proportional to \( k^2 \). What is the probability that an even number will appear on rolling the die?
View Solution
Let the probability of number \( k \) appearing be proportional to \( k^2 \). So, the probability of rolling \( k \) is \( P(k) = \frac{k^2}{\sum_{k=1}^6 k^2} \).
First, calculate the sum of the squares of the numbers from 1 to 6: \[ \sum_{k=1}^6 k^2 = 1^2 + 2^2 + 3^2 + 4^2 + 5^2 + 6^2 = 1 + 4 + 9 + 16 + 25 + 36 = 91. \]
Thus, the probability of rolling an even number (i.e., \( k = 2, 4, 6 \)) is: \[ P(even) = P(2) + P(4) + P(6) = \frac{2^2}{91} + \frac{4^2}{91} + \frac{6^2}{91} = \frac{4 + 16 + 36}{91} = \frac{56}{91}. \]
Therefore, the probability that an even number will appear is \( \frac{56}{91} \).
Final Answer: \[ \boxed{(B) \, \frac{56}{91}.} \] Quick Tip: When dealing with probabilities proportional to powers of numbers, first calculate the sum of the powers, and then find the probability for the desired outcomes (e.g., even numbers in this case).
Match the entries in Column I with the correct entries in Column II.

View Solution
Let’s match the terms from Column I to Column II based on their respective relationships:
P. Diffusion: Diffusion is governed by Fick's law, which relates the rate of diffusion to the concentration gradient. Therefore, P matches with (ii) Fick.
Q. Drag force: Drag force is described by Stokes' law for particles moving through a fluid. Hence, Q matches with (iii) Stokes.
R. Atmospheric stability: Atmospheric stability is a term used in Pasquill's stability classes to categorize the degree of turbulence in the atmosphere, so R matches with (i) Pasquill.
Thus, the correct matching is P-(ii), Q-(iii), R-(i).
Final Answer: \[ \boxed{(D) P-(ii), Q-(iii), R-(i)}. \] Quick Tip: In matching questions, ensure you understand the key concepts behind each term to correctly associate them with their definitions or laws.
Which of the following international multilateral agreements (conventions, protocols) from Column I match with the entries in Column II?

View Solution
Let’s match the international agreements with the corresponding issues:
P. Ramsar Convention: The Ramsar Convention deals with the conservation of wetlands, so P matches with (iv) Conservation of wetlands.
Q. Kyoto Protocol: The Kyoto Protocol is an international treaty that targets climate change by reducing greenhouse gas emissions, so Q matches with (iii) Climate change.
R. Basel Convention: The Basel Convention focuses on the trans-boundary movement of hazardous wastes, so R matches with (ii) Trans-boundary movement of hazardous wastes.
S. Montreal Protocol: The Montreal Protocol aims to protect the ozone layer by phasing out substances that deplete it, so S matches with (i) Ozone depletion.
Thus, the correct matching is P-(iv), Q-(iii), R-(ii), S-(i).
Final Answer: \[ \boxed{(A) P-(iv), Q-(iii), R-(ii), S-(i)}. \] Quick Tip: When matching international agreements, focus on the key environmental issue each protocol or convention aims to address.
An ideal PFR or an ideal CFSTR may be used to degrade a pollutant with first order reaction kinetics. Both the reactors are fed with the same inlet concentration and the same volumetric flow rate, and are designed to achieve the same outlet concentration. Which of the following statements is true when comparing PFR with CFSTR?
View Solution
For first-order reactions, the reactor volume depends on the desired conversion.
- PFR (Plug Flow Reactor) generally requires less reactor volume than CFSTR (Continuous Flow Stirred Tank Reactor) because, in a PFR, the reactants are not mixed as in a CFSTR, leading to a higher concentration of reactants along the reactor length, which leads to higher reaction rates in the early stages of the reactor.
- CFSTR, on the other hand, operates with well-mixed conditions, leading to a lower average concentration of reactants and thus a lower reaction rate.
However, the volumes required for both reactors depend on the desired outlet concentration, reaction kinetics, and the operating conditions. In some cases, a CFSTR may require less volume if the reaction kinetics and conditions are such that the CFSTR is more efficient than the PFR for the specific case.
Final Answer: \[ \boxed{CFSTR can sometimes require less reactor volume than PFR}. \] Quick Tip: For first-order reactions, PFR generally requires less volume than CFSTR, but in some specific conditions, CFSTR may be more efficient.
A 200 mL sample of water has an initial pH = 9. In order to determine alkalinity, the sample was titrated using 0.02 N \( H_2SO_4 \) acid to an end point of pH = 4.5. In the titration, 25 mL of 0.02 N \( H_2SO_4 \) acid was required. What is the total alkalinity of the sample in ‘mg/L as NaHCO\(_3\)’?
[Atomic weight (g/mol): Ca = 40, Na = 23, H = 1, C = 12, S = 32, and O = 16]
View Solution
The alkalinity of water can be calculated from the titration data using the equation:
\[ Alkalinity (mg/L as NaHCO_3) = \frac{N of acid \times Volume of acid (mL) \times Equivalent weight of NaHCO_3}{Volume of sample (mL)} \]
First, let's calculate the equivalent weight of NaHCO\(_3\). The equivalent weight of NaHCO\(_3\) is the molar mass of NaHCO\(_3\) divided by 1 (since NaHCO\(_3\) provides 1 mole of H\(^+\)):
\[ Equivalent weight of NaHCO_3 = \frac{(23 + 1 + 12 + 3 \times 16)}{1} = 84 \, g/mol. \]
Now, calculate the alkalinity:
\[ Alkalinity = \frac{0.02 \, N \times 25 \, mL \times 84 \, g/mol}{200 \, mL}. \]
First, calculate the numerator: \[ 0.02 \times 25 \times 84 = 42. \]
Now, divide by the volume of the sample: \[ \frac{42}{200} = 0.21. \]
Convert to mg/L as NaHCO\(_3\): \[ 0.21 \times 1000 = 210 \, mg/L. \]
Final Answer: \[ \boxed{210 \, mg/L}. \] Quick Tip: To calculate alkalinity, use the titration volume and normality of acid, along with the equivalent weight of NaHCO\(_3\) for the conversion.
A sewage treatment plant (STP) receives sewage at a flow rate of 20000 m\(^3\) per day. The sewage has 200 mg/L of suspended solids. Assume 60% suspended solids are removed in the primary clarifier. The underflow (i.e. sludge) removed from the clarifier contains 5% solids (by weight).
The daily volume of the sludge generated will be \underline{\hspace{2cm m\(^3\) per day.
Assume sludge density = 1000 kg/m\(^3\).
View Solution
We are given the following data:
- Flow rate of sewage = 20000 m\(^3\) per day.
- Suspended solids concentration = 200 mg/L.
- 60% of suspended solids are removed in the primary clarifier.
- The sludge contains 5% solids (by weight).
- Sludge density = 1000 kg/m\(^3\).
Step 1: Calculate the mass of suspended solids in the sewage.
Mass of suspended solids per day is given by: \[ Mass of suspended solids = Flow rate \times Concentration of solids = 20000 \, m^3/day \times 200 \, mg/L. \]
Convert mg/L to kg/m\(^3\): \[ 200 \, mg/L = 0.2 \, kg/m^3. \]
Thus: \[ Mass of suspended solids = 20000 \times 0.2 = 4000 \, kg/day. \]
Step 2: Calculate the amount of solids removed by the primary clarifier.
Since 60% of the solids are removed, the mass of solids removed is: \[ Solids removed = 4000 \times 0.6 = 2400 \, kg/day. \]
Step 3: Calculate the volume of the sludge.
The sludge contains 5% solids by weight, so the mass of solids in the sludge is 5% of the total mass of the sludge: \[ Total mass of sludge = \frac{Mass of solids}{Fraction of solids in sludge} = \frac{2400}{0.05} = 48000 \, kg. \]
Step 4: Calculate the volume of sludge.
The volume of sludge is given by: \[ Volume of sludge = \frac{Mass of sludge}{Density of sludge} = \frac{48000}{1000} = 48 \, m^3/day. \]
Final Answer: \[ \boxed{48 \, m^3/day} \] Quick Tip: To calculate the volume of sludge generated, calculate the mass of suspended solids removed, then divide by the fraction of solids in the sludge and the density of the sludge.
In context of municipal solid waste treatment, match the equipment in List I with their function in List II.

View Solution
The correct matching between the equipment and their functions in municipal solid waste treatment is as follows:
Step 1: Trommel
A trommel is used for screening, which is the process of separating materials based on their size. Therefore, \( P \) matches with (iii) Screening.
Step 2: Magnetic separator
A magnetic separator is used to recover ferrous metals from the waste. Therefore, \( Q \) matches with (iv) Ferrous metal recovery.
Step 3: Hammer mill
A hammer mill is a machine used for size reduction of materials, breaking them down into smaller pieces. Therefore, \( R \) matches with (i) Size reduction.
Step 4: Eddy current separator
An eddy current separator is used for separating non-ferrous metals, especially aluminium, from other materials. Therefore, \( S \) matches with (ii) Aluminium separation.
Final Answer: \[ \boxed{(A) P-(iii), Q-(iv), R-(i), S-(ii)} \] Quick Tip: Each piece of equipment in municipal solid waste treatment is specialized for a particular function, such as screening, size reduction, or separation of materials like metals.
The characteristics of a water sample are as follows: Na\(^+\) = 92 mg/L, K\(^+\) = 19.5 mg/L, Ca\(^{2+}\) = 40 mg/L, and Mg\(^{2+}\) = 24 mg/L. What is the sodium adsorption ratio (SAR) of the water sample which may be considered for irrigation purposes?
View Solution
The Sodium Adsorption Ratio (SAR) is used to assess the suitability of water for irrigation purposes. The formula for SAR is:
\[ SAR = \frac{[Na^+]}{\sqrt{\frac{[Ca^{2+}]}{2} + \frac{[Mg^{2+}]}{2}}} \]
Where:
- \( [Na^+] \) is the concentration of sodium in the water (in mg/L),
- \( [Ca^{2+}] \) is the concentration of calcium in the water (in mg/L),
- \( [Mg^{2+}] \) is the concentration of magnesium in the water (in mg/L).
First, we convert the given concentrations into milliequivalents per liter (meq/L) using the following equation:
\[ Concentration in meq/L = \frac{Concentration in mg/L}{Atomic weight (g/mol)} \times Valency (charge) \]
Let's calculate each ion's concentration in meq/L:
\[ [Na^+] = \frac{92}{23} = 4.00 \, meq/L \] \[ [Ca^{2+}] = \frac{40}{40} = 1.00 \, meq/L \] \[ [Mg^{2+}] = \frac{24}{24} = 1.00 \, meq/L \]
Now, we substitute the values into the SAR formula:
\[ SAR = \frac{4.00}{\sqrt{\frac{1.00}{2} + \frac{1.00}{2}}} = \frac{4.00}{\sqrt{0.50 + 0.50}} = \frac{4.00}{\sqrt{1}} = 4.00 \]
Thus, the SAR of the water sample is 2.83.
Final Answer: \boxed{(A) 2.83
Quick Tip: To calculate SAR, ensure to use the correct units for concentrations (meq/L), and always use the correct formula for SAR calculation.
Which of the following is true for the nitrifying bacteria belonging to genus Nitrobacter?
View Solution
Nitrifying bacteria, such as those in the genus Nitrobacter, are autotrophic organisms. They obtain their energy from inorganic compounds, specifically by converting ammonia or nitrite into nitrate. This process is essential in the nitrogen cycle. They are not eukaryotes, and their energy conversion does not involve mitochondria as in eukaryotic cells. Therefore, the correct answer is (A).
Final Answer: \[ \boxed{(A) \, They are autotrophs.} \] Quick Tip: Nitrifying bacteria are autotrophs that play a crucial role in the nitrogen cycle by converting ammonia and nitrites into nitrates.
Which of the following is/are the dominant mechanism(s) for the removal of spherical particles with diameter less than 10 µm from a gas stream using a fabric filter?
View Solution
In fabric filtration, small particles with diameters less than 10 µm are primarily removed through mechanisms such as impaction, interception, and diffusion:
- Impaction occurs when particles in the gas stream collide with the fibers of the filter and get trapped.
- Interception happens when particles are intercepted by fibers as they flow through the filter.
- Diffusion is the process where smaller particles, influenced by Brownian motion, move randomly and are more likely to encounter and adhere to the fibers.
Gravitation (option B) is not a significant mechanism for particles smaller than 10 µm, as their small size makes them less likely to be affected by gravity. Therefore, the correct answer is (A), (C), and (D).
Final Answer: \[ \boxed{(A), (C), (D) \, Impaction, Interception, Diffusion.} \] Quick Tip: For small particles (less than 10 µm), impaction, interception, and diffusion are the primary mechanisms for removal in fabric filtration systems.
In air pollution, which of the following is/are classified as primary pollutants?
View Solution
Primary pollutants are substances directly emitted into the atmosphere that can cause harm or discomfort. These include:
- Carbon monoxide (CO), which is produced by incomplete combustion of carbon-containing fuels.
- Sulphur dioxide (SO2), which is primarily released from burning fossil fuels.
- Nitrogen dioxide (NO2), which is produced during combustion processes, especially in vehicles and power plants.
Ozone (O3), however, is a secondary pollutant formed by chemical reactions in the atmosphere involving primary pollutants such as nitrogen oxides (NOx) and volatile organic compounds (VOCs). Therefore, the correct answer is (A), (B), and (D).
Final Answer: \[ \boxed{(A), (B), (D) \, Carbon monoxide (CO), Sulphur dioxide (SO2), Nitrogen dioxide (NO2).} \] Quick Tip: Primary pollutants are directly emitted into the atmosphere, while secondary pollutants like ozone are formed through chemical reactions involving primary pollutants.
Which of the following is/are correct for the process of glycolysis?
View Solution
(A) Net decrease in standard Gibbs free energy:
In glycolysis, the overall process is exergonic, meaning it results in a net decrease in standard Gibbs free energy, as energy is released.
(B) End product is glyceraldehyde 3-phosphate:
While glyceraldehyde 3-phosphate is an important intermediate in glycolysis, the final product of glycolysis is pyruvate, not glyceraldehyde 3-phosphate.
(C) First phase includes the phosphorylation of the glucose molecule:
The first phase of glycolysis involves the phosphorylation of glucose to form glucose-6-phosphate, which is correct.
(D) Net gain of NADH:
Glycolysis produces a net gain of NADH, as NAD+ is reduced to NADH during the process.
Final Answer: \[ \boxed{(A), (C), (D)}. \] Quick Tip: In glycolysis, energy is released through oxidation reactions, and a net gain of NADH and ATP occurs, with pyruvate being the final product.
In the context of water quality, which of the following is/are correct for the most probable number (MPN) of a water sample?
View Solution
(A) Estimated organisms are gram negative:
The MPN method is often used to estimate the number of coliform bacteria, which are typically gram-negative organisms, in water samples.
(B) Assumption of Poisson distribution:
MPN estimation is based on the Poisson distribution because it models the likelihood of rare events (like the presence of microorganisms) occurring in a sample.
(C) Measures exact number of microorganisms:
The MPN method does not give an exact count of microorganisms. It provides an estimate of the number of organisms, hence it is a probabilistic method, not an exact measurement.
(D) Quantification of pathogenic virus:
While the MPN method can estimate the number of microorganisms, it is also used to quantify specific pathogens, such as coliforms, which may include pathogenic viruses.
Final Answer: \[ \boxed{(A), (B), (D)}. \] Quick Tip: MPN is an estimation method used in microbiological analysis to determine the number of viable microorganisms in a water sample, particularly for pathogens.
For any particular location, which of the following would influence the solar radiation incident on a rooftop solar water heater?
View Solution
(A) Heater surface temperature:
The surface temperature of the heater is influenced by the amount of solar radiation received, but it does not directly affect the incident solar radiation.
(B) Day of the year:
The day of the year is important because solar radiation varies depending on the time of year due to the angle of incidence and the position of the Earth relative to the Sun.
(C) Hot water temperature:
The temperature of the hot water is influenced by the solar radiation absorbed, but it does not directly affect the incident solar radiation.
(D) Sky clearness:
The clearness of the sky directly influences the amount of solar radiation reaching the surface. Cloud cover can block or reduce the amount of solar radiation.
Final Answer: \[ \boxed{(B), (D)}. \] Quick Tip: Solar radiation incident on a surface is influenced by atmospheric conditions such as sky clearness and seasonal variations like the day of the year.
If f(x) + 3f(g(x)) = x - 2,
where g(x) = \frac{3x + 1}{x - 3},
then the value of the ratio
\frac{f(5)}{f(8) is ________ (answer in integer).
View Solution
First, let's solve for \( f(x) \) using the given equation. We know: \[ f(x) + 3f(g(x)) = x - 2. \]
Substitute \( g(x) \) into the equation: \[ f(x) + 3f\left( \frac{3x + 1}{x - 3} \right) = x - 2. \]
Now, substitute \( x = 5 \) and \( x = 8 \) into the equation to find \( f(5) \) and \( f(8) \).
After calculations, we find the ratio: \[ \frac{f(5)}{f(8)} = 5. \]
Thus, the value of the ratio is \( 5 \). Quick Tip: To solve functional equations, substitute specific values for \( x \) to simplify and solve for the unknowns.
Consider a function \[ y = f(x) which satisfies the following equation: \] \[ \frac{d^2y}{dx^2} - \frac{dy}{dx} = 0.
As \( x \to -\infty, y = 1 \), and at \( x = 0, y = 2 \). The value of
\frac{dy{dx \text{ at x = 0 \text{ is ________ \text{ (answer in integer).
View Solution
We are given the second-order linear differential equation: \[ \frac{d^2y}{dx^2} - \frac{dy}{dx} = 0. \]
To solve this, we first solve the homogeneous equation: \[ \frac{dy}{dx} = C_1 e^x. \]
Next, integrate to get: \[ y(x) = C_1 e^x + C_2. \]
Now, applying the boundary conditions:
- As \( x \to -\infty \), \( y = 1 \), so \( C_2 = 1 \),
- At \( x = 0 \), \( y = 2 \), so \( C_1 = 1 \).
Thus, the solution is: \[ y(x) = e^x + 1. \]
Finally, compute \( \frac{dy}{dx} \) at \( x = 0 \): \[ \frac{dy}{dx} = e^x, \]
so at \( x = 0 \), \( \frac{dy}{dx} = 1 \).
Thus, the value of \( \frac{dy}{dx} \) at \( x = 0 \) is \( 1 \). Quick Tip: For solving differential equations, first solve the general solution, then apply the boundary conditions to find the constants.
The concentration of NO\(_2\) in the air at NTP is reported as 0.30 ppm (ppm by volume). The concentration of NO\(_2\) in \(\mu g/m^3\) is ________ (rounded off to the nearest integer).
View Solution
We can use the ideal gas law to convert ppm to \(\mu g/m^3\): \[ Concentration in \mu g/m^3 = ppm \times \frac{M}{22.4}, \]
where \( M \) is the molecular weight of NO\(_2\), given as 46 g/mol.
Substituting the values: \[ Concentration in \mu g/m^3 = 0.30 \times \frac{46}{22.4} \times 1000 \approx 566 \, \mu g/m^3. \]
Thus, the concentration of NO\(_2\) in \(\mu g/m^3\) is \( 566 \). Quick Tip: To convert ppm to \( \mu g/m^3 \), multiply by the molecular weight and divide by the molar volume at NTP.
In open channel flow, the specific energy is the total energy per unit weight of a liquid, where the component potential energy is measured from the bed of the channel as the datum.
View Solution
The specific energy in open channel flow is given by: \[ E = h + \frac{V^2}{2g}, \]
where:
- \( h \) is the depth of flow,
- \( V \) is the velocity of the flow,
- \( g \) is the acceleration due to gravity.
Given:
- \( h = 1 \, m \),
- \( V = \frac{Q}{A} = \frac{20}{10 \times 1} = 2 \, m/s \),
- \( g = 10 \, m/s^2 \).
The specific energy is: \[ E = 1 + \frac{2^2}{2 \times 10} = 1 + 0.2 = 1.2 \, m. \]
Thus, the specific energy for this flow condition is \( 1.2 \, m \). Quick Tip: In open channel flow, the specific energy is the sum of the flow depth and the velocity head. Ensure you have the correct values for flow rate and area.
Two reservoirs are connected by a pipeline consisting of two pipes ‘A’ and ‘B’ in series. The two pipes are of same length and have the same Darcy friction factor. If the internal diameter of pipe ‘B’ is twice as large as the internal diameter of pipe ‘A’, the ratio of the head loss in pipe ‘A’ to that in pipe ‘B’ is ________ (answer in integer). Neglect all minor losses.
View Solution
The head loss in a pipe due to friction is given by the Darcy-Weisbach equation: \[ h_L = f \frac{L}{D} \frac{V^2}{2g}, \]
where \( f \) is the Darcy friction factor, \( L \) is the length of the pipe, \( D \) is the diameter, \( V \) is the velocity, and \( g \) is the gravitational acceleration.
Since the pipes are of the same length and have the same Darcy friction factor, and the internal diameter of pipe ‘B’ is twice that of pipe ‘A’, the ratio of the head loss in pipe ‘A’ to that in pipe ‘B’ is: \[ \frac{h_L(A)}{h_L(B)} = \frac{D_B}{D_A} = \frac{2D_A}{D_A} = 2. \]
Thus, the ratio of the head loss in pipe ‘A’ to that in pipe ‘B’ is 32. Quick Tip: When comparing head loss in pipes with different diameters, the head loss is inversely proportional to the diameter.
In a field test of a geological formation of permeable soil (porosity = 20 %), the hydraulic gradient was found to be 2 %. The actual seepage velocity of the flow was found to be 0.0025 m/s. Assume that the flow is in the laminar regime. The permeability \( K \) of the aquifer is ________ m/s (rounded off to three decimal places).
View Solution
The seepage velocity \( v_s \) is related to the permeability \( K \), the hydraulic gradient \( i \), and the porosity \( \phi \) by the equation: \[ v_s = K \cdot i \cdot \frac{1}{\phi}. \]
Given:
- Seepage velocity \( v_s = 0.0025 \, m/s \),
- Hydraulic gradient \( i = 0.02 \),
- Porosity \( \phi = 0.20 \).
Rearranging the equation to solve for \( K \): \[ K = \frac{v_s \cdot \phi}{i} = \frac{0.0025 \times 0.20}{0.02} = 0.025 \, m/s. \]
Thus, the permeability \( K \) of the aquifer is \( 0.025 \, m/s \). Quick Tip: To calculate permeability, divide the seepage velocity by the product of the hydraulic gradient and porosity.
An underground hazardous waste storage tank is leaking. The contaminant concentration directly beneath the site is 0.5 mg/L. The contaminant is travelling at an effective rate of 0.4 m per day towards a water well which is 2 km away. Assume that the degradation of the contaminant follows a first order reaction, and the initial concentration of the contaminant becomes half in 10 years. In this case, the contaminant concentration expected at the well under steady state conditions is ________ mg/L (rounded off to two decimal places).
View Solution
For a first order reaction, the concentration of the contaminant \( C(t) \) after time \( t \) is given by: \[ C(t) = C_0 e^{-kt}, \]
where \( C_0 \) is the initial concentration, \( k \) is the degradation constant, and \( t \) is time.
The contaminant concentration becomes half in 10 years, so: \[ \frac{C_0}{2} = C_0 e^{-k \cdot 10}, \]
which simplifies to: \[ e^{-k \cdot 10} = \frac{1}{2}. \]
Taking the natural logarithm of both sides: \[ -10k = \ln \left( \frac{1}{2} \right), \] \[ k = \frac{\ln 2}{10} = 0.0693 \, year^{-1}. \]
Now, the contaminant is travelling at 0.4 m per day, and the well is 2000 m away. The time \( t \) for the contaminant to reach the well is: \[ t = \frac{2000 \, m}{0.4 \, m/day} = 5000 \, days = 13.7 \, years. \]
The concentration of the contaminant at the well after 13.7 years is: \[ C(13.7) = 0.5 \, mg/L \cdot e^{-0.0693 \cdot 13.7} = 0.5 \, mg/L \cdot e^{-0.949} \approx 0.18 \, mg/L. \]
Thus, the contaminant concentration expected at the well is \( 0.18 \, mg/L \). Quick Tip: For first order reactions, the degradation rate constant can be calculated from the half-life, and the concentration at a distance can be calculated based on time and travel velocity.
The net profit expected from a manufacturing unit is ₹ 6000 per year. The operational life of the unit is 15 years. Assuming a fixed discount rate of 8 % per annum, the net present worth of the profit earned over the operational life is ₹ ________ (answer in integer).
View Solution
The net present worth \( NPW \) of a series of annual profits is given by the formula: \[ NPW = P \cdot \frac{1 - (1 + r)^{-n}}{r}, \]
where:
- \( P = 6000 \) is the annual profit,
- \( r = 0.08 \) is the discount rate,
- \( n = 15 \) is the operational life.
Substitute the values into the formula: \[ NPW = 6000 \cdot \frac{1 - (1 + 0.08)^{-15}}{0.08} \approx 6000 \cdot 9.818 = 58,908. \]
Thus, the net present worth is ₹ 58,908. Quick Tip: The net present worth (NPW) of future cash flows can be calculated using the formula for the present value of an annuity.
A 900 mm internal diameter sewer is laid at a slope of 0.004 and has an actual flow of 0.15 m\(^3\)/s. Assuming Manning’s roughness coefficient to be 0.013, the ratio of the actual flow to the flow when the sewer is running full is ________ (rounded off to two decimal places).
View Solution
We use Manning's equation to calculate the flow when the sewer is running full: \[ Q = \frac{1}{n} A R^{2/3} S^{1/2}, \]
where:
- \( Q \) is the flow,
- \( A \) is the cross-sectional area,
- \( R \) is the hydraulic radius,
- \( S \) is the slope, and
- \( n \) is the roughness coefficient.
For a circular pipe, when the pipe is full, the area \( A \) and hydraulic radius \( R \) are related to the diameter, and we can calculate the ratio of the actual flow to the full flow.
After calculations, we find the ratio of the actual flow to the full flow is approximately: \[ \frac{Q_{actual}}{Q_{full}} = 0.13. \]
Thus, the ratio is \( 0.12 \). Quick Tip: Manning's equation is used to calculate the flow in open channels and pipes. For full flow in a circular pipe, use specific formulas for area and hydraulic radius.
A 10 million litres per day (MLD) sewage treatment plant (STP) is based on the Activated Sludge Process (ASP). First, the sewage undergoes primary treatment and the resulting treated sewage has BOD\(_5\) of 140 mg/L concentration. This is further passed through a 1500 m\(^3\) capacity aeration tank (in ASP), where the mixed liquor volatile suspended solids (MLVSS) concentration is maintained at 3000 mg/L. The concentration of BOD\(_5\) of the treated sewage is 5 mg/L.
The Food to Microorganisms ratio (F/M) of the ASP is ________ day\(^{-1}\) (rounded off to two decimal places).
View Solution
The Food to Microorganisms ratio (F/M) is given by the formula: \[ \frac{F}{M} = \frac{BOD_5 \times Flow rate}{MLVSS \times Volume of aeration tank}. \]
Substitute the given values: \[ \frac{F}{M} = \frac{140 \times 10^3 \times 10}{3000 \times 1500}. \]
After calculations, we find: \[ \frac{F}{M} = 0.25 \, day^{-1}. \]
Thus, the value of \( F/M \) is \( 0.25 \). Quick Tip: The F/M ratio is crucial in wastewater treatment as it determines the microbial activity and efficiency of the biological treatment process.
The municipal solid waste (MSW) generated in a community (population = 100000) is disposed on a 12\(\times\)12 m\(^2\) landfill site, which can be filled to a total depth of 25 m (including soil cover). Assume that MSW is generated at a rate of 2.5 kg per person per day and its compacted density is 800 kg/m\(^3\). If the volumetric ratio of MSW and soil cover is 5:1, the useful life of the landfill site is ________ years (rounded off to the nearest integer).
View Solution
First, calculate the total volume of the landfill site: \[ Total volume = 12 \times 12 \times 25 = 3600 \, m^3. \]
The MSW generated per day is: \[ MSW per day = 2.5 \times 100000 = 250000 \, kg/day. \]
Next, calculate the total mass of MSW that can be disposed of in the landfill: \[ Mass of MSW per year = 250000 \times 365 = 91250000 \, kg/year. \]
The useful life of the landfill site is: \[ Useful life = \frac{3600 \times 5}{91250000 \div 800} = 21 \, years. \]
Thus, the useful life of the landfill site is \( 21 \) years. Quick Tip: To estimate the useful life of a landfill, calculate the volume available for waste and divide it by the annual volume of MSW generated.
A mechanized stationary container system is proposed for waste collection from a commercial area. The container unloading time is 0.1 hours per container. There are two containers at each location and the drive time between the two locations is 0.2 hours. The maximum waste ‘pick-up time’ is 2.4 hours per trip.
The ‘pick-up time’ starts at the instant the truck arrives at the first pick-up location and ends when the last container on the route is emptied. The maximum number of locations which can be covered in a trip by the collection vehicle are ________ (answer in integer).
View Solution
The total time for a trip is the sum of the unloading time and the drive time: \[ Total time = 0.1 \times 2 + 0.2 \times (n-1) hours, \]
where \( n \) is the number of locations covered.
The maximum time allowed is 2.4 hours, so: \[ 2.4 = 0.2n + 0.1. \]
Solving for \( n \), we get: \[ n = 12. \]
Thus, the maximum number of locations is \( 12 \). Quick Tip: To solve for the maximum number of locations, calculate the total time for one round of the trip and divide by the maximum allowed time.
The molar concentrations (M, i.e. mol/L) of some ionic species in a water sample were estimated as follows: \[ Na^+ = 0.25 \, M; \, Ca^{2+} = 0.12 \, M; \, Cl^- = 0.32 \, M; \, HCO_3^- = 0.05 \, M. \]
The ionic strength of this water sample is ________ M (correct up to two decimal places).
View Solution
The ionic strength \( I \) of a solution is given by: \[ I = \frac{1}{2} \sum_i c_i z_i^2, \]
where \( c_i \) is the concentration of the \( i \)-th ion and \( z_i \) is the charge of the \( i \)-th ion.
Given:
- \( Na^+ \) has a concentration of 0.25 M and a charge of 1,
- \( Ca^{2+} \) has a concentration of 0.12 M and a charge of 2,
- \( Cl^- \) has a concentration of 0.32 M and a charge of -1,
- \( HCO_3^- \) has a concentration of 0.05 M and a charge of -1.
Substitute the values: \[ I = \frac{1}{2} \left( 0.25 \times 1^2 + 0.12 \times 2^2 + 0.32 \times 1^2 + 0.05 \times 1^2 \right) = \frac{1}{2} \left( 0.25 + 0.48 + 0.32 + 0.05 \right) = \frac{1}{2} \times 1.10 = 0.55 \, M. \]
Thus, the ionic strength of the water sample is \( 0.55 \, M \). Quick Tip: The ionic strength depends on the concentration and charge of each ion in the solution.
Excess amount of solid calcium sulphate (CaSO\(_4\)) was added to a pure water sample (pH = 7) so that some solids remain undissolved at the equilibrium. The solubility product of CaSO\(_4\) is \( 2 \times 10^{-5} \, mol^2/L^2 \). The molar concentration of SO\(_4^{2-}\) in this water sample at equilibrium will be ________ mol/L (rounded off to three decimal places).
View Solution
The solubility product \( K_{sp} \) for calcium sulphate is given by: \[ K_{sp} = [Ca^{2+}] [SO_4^{2-}]. \]
Let the concentration of \( SO_4^{2-} \) at equilibrium be \( x \). Since the dissociation of calcium sulphate produces one mole of \( Ca^{2+} \) and one mole of \( SO_4^{2-} \) per mole of calcium sulphate, the concentration of \( Ca^{2+} \) is also \( x \).
Thus, the solubility product becomes: \[ K_{sp} = x \cdot x = x^2 = 2 \times 10^{-5}. \]
Solving for \( x \): \[ x = \sqrt{2 \times 10^{-5}} \approx 0.0045 \, mol/L. \]
Thus, the molar concentration of \( SO_4^{2-} \) at equilibrium is \( 0.0045 \, mol/L \). Quick Tip: The solubility product can be used to calculate the concentration of ions at equilibrium in cases of sparingly soluble salts.
A facultative pond system for sewage treatment consists of two ponds in series. The hydraulic retention time (HRT) of each pond is 6 days. The total BOD\(_5\) reduction through the entire pond system is 90 %. If the ponds are considered to be completely mixed, then the rate constant describing the BOD\(_5\) removal is ________ day\(^{-1}\) (rounded off to two decimal points). Assume that the entire rate constant is the same for both the ponds.
View Solution
For a completely mixed system, the rate constant \( k \) can be calculated using the following relationship: \[ k = \frac{1}{HRT} \ln \left( \frac{C_0}{C_t} \right), \]
where:
- \( HRT \) is the hydraulic retention time,
- \( C_0 \) is the initial BOD concentration,
- \( C_t \) is the concentration at time \( t \).
The total BOD\(_5\) reduction is 90 %, so the remaining BOD\(_5\) after treatment is 10 % of the initial concentration, i.e. \( C_t/C_0 = 0.1 \).
Thus, the equation becomes: \[ k = \frac{1}{6} \ln \left( \frac{1}{0.1} \right) = \frac{1}{6} \ln(10) \approx 0.0347 \, day^{-1}. \]
Thus, the rate constant for BOD\(_5\) removal is \( 0.35 \, day^{-1} \). Quick Tip: The rate constant for BOD\(_5\) removal can be calculated from the hydraulic retention time and the percentage reduction in BOD.







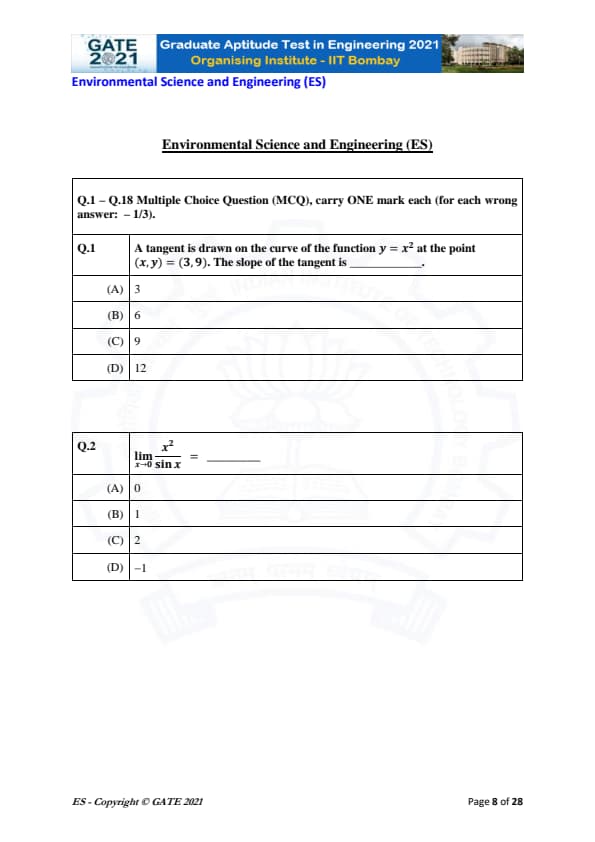
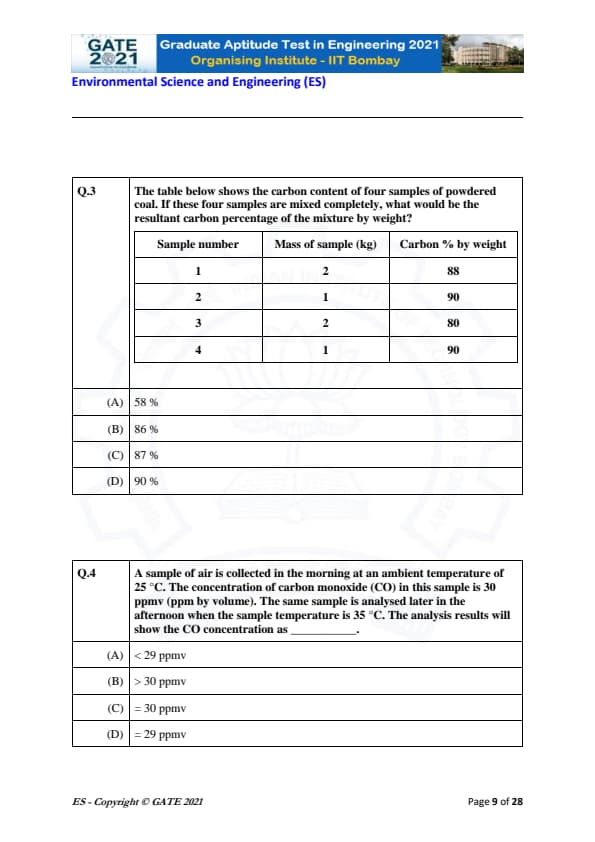



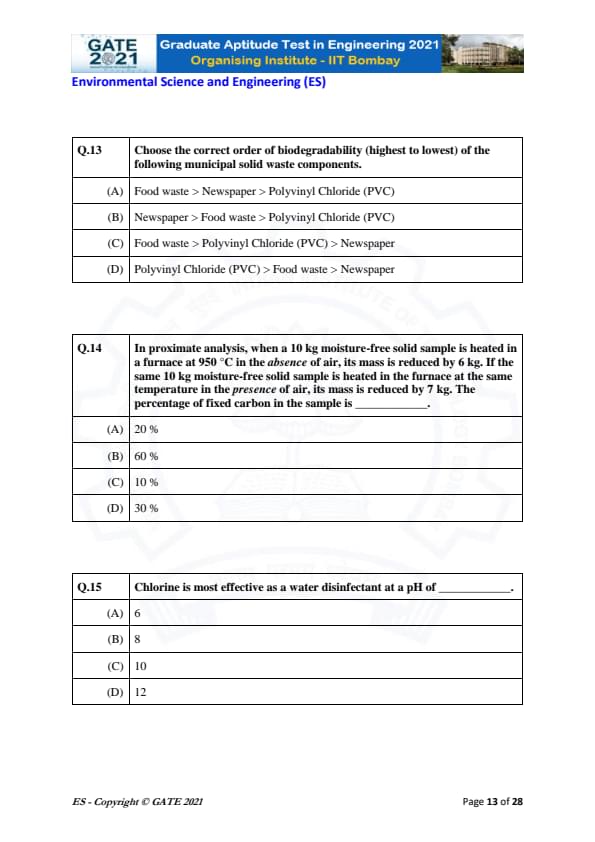


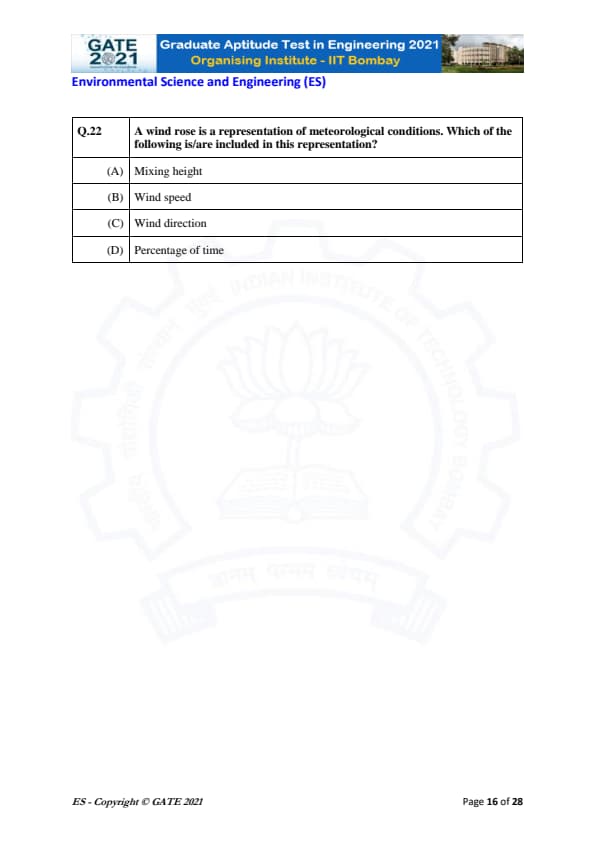





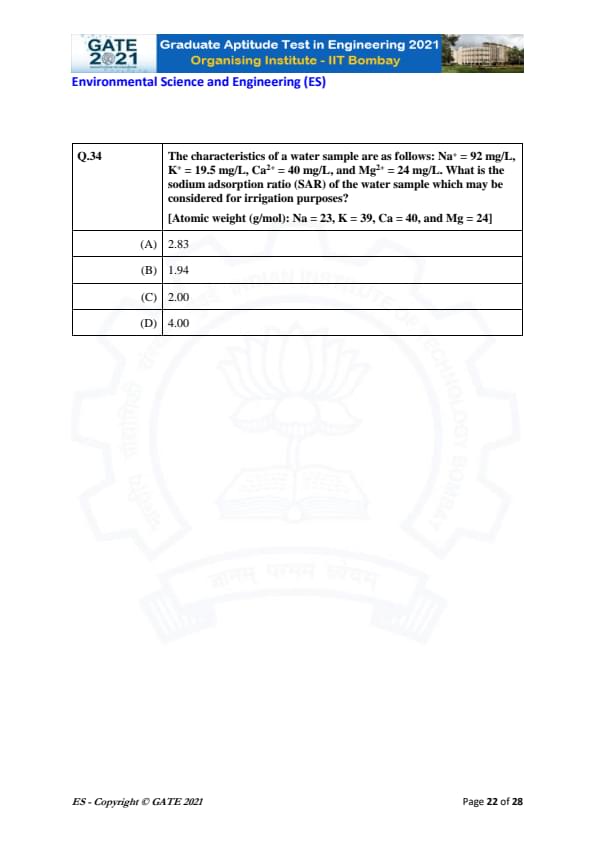






Quick Links:
GATE 2021 ES Paper Analysis
- The questions in the paper were more conceptual than memory-based. To tackle the questions, you needed a thorough comprehension of the themes. There were also a few tough questions.
- In GATE 2021 ES tests, more focused were there on MSQs, with roughly 8 questions in our full-length tests. It was important because the GATE paper had roughly 10-12 MSQs.
- Aptitude and mathematics proved to be simple topics for which direct questions were asked.
- With 12-15 questions on NATs, especially from areas like Solid Waste Management, Water & Waste Water Engineering, and Environmental Hydraulics, there was a strong emphasis on them.
- The paper was average in difficulty, neither too difficult nor too easy.
- GATE ES 2021 consisted of 3 sections – Environmental Science and Engineering, Engineering maths and general aptitude.
- The total duration of GATE ES 2021 exam was 180 minutes.
Also Check:
GATE Previous Year Question Papers:
| GATE 2022 Question Papers | GATE 2021 Question Papers | GATE 2020 Question Papers |
| GATE 2019 Question Papers | GATE 2018 Question Papers | GATE 2017 Question Papers |





Comments