Maharashtra Board Class 10 Mathematics Geometry Part-2 Question Paper 2025 (Code N 819) Available- Download Here with Solution PDF

Out of the following which is a Pythagorean triplet ?

• (A) (1, 5, 10)
• (B) (3, 4, 5)
• (C) (2, 2, 2)
• (D) (5, 5, 2)

\(\angle\)ACB is inscribed angle in a circle with centre O. If \(\angle\)ACB = 65\(^{\circ}\), then what is measure of its intercepted arc AXB ?

• (A) 65\(^{\circ}\)
• (B) 230\(^{\circ}\)
• (C) 295\(^{\circ}\)
• (D) 130\(^{\circ}\)

Distance of point (3, 4) from the origin is .................... .

• (A) 7
• (B) 1
• (C) 5
• (D) -5

If radius of cone is 5 cm and its perpendicular height is 12 cm, then the slant height is .................... .

• (A) 17 cm
• (B) 4 cm
• (C) 13 cm
• (D) 60 cm

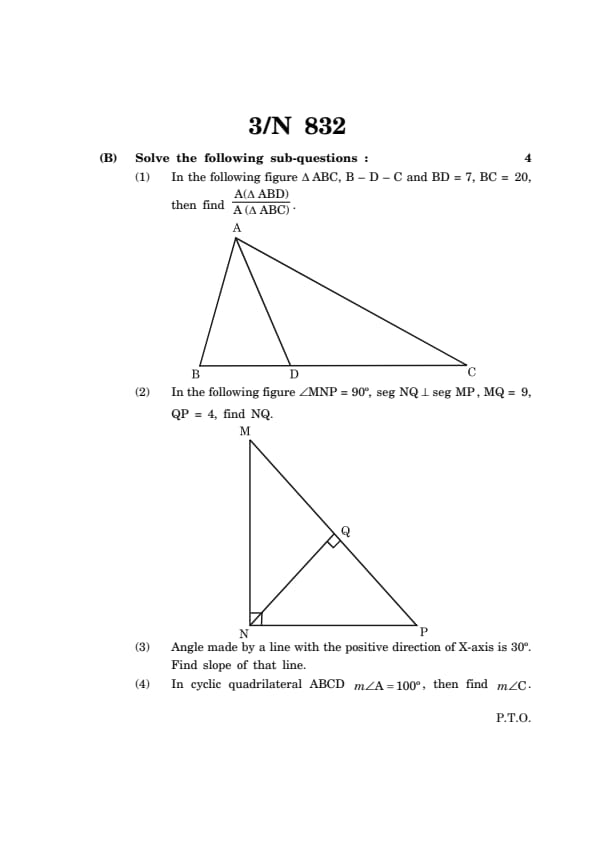
In the following figure \(\triangle\) ABC, B-D-C and BD = 7, BC = 20, then find \(\frac{A(\triangle ABD)}{A(\triangle ABC)}\).

In the following figure \(\angle\)MNP = 90\(^\circ\), seg NQ \(\perp\) seg MP, MQ = 9, QP = 4, find NQ.

Angle made by a line with the positive direction of X-axis is 30\(^\circ\). Find slope of that line.

In cyclic quadrilateral ABCD m\(\angle\)A = 100\(^\circ\), then find m\(\angle\)C.

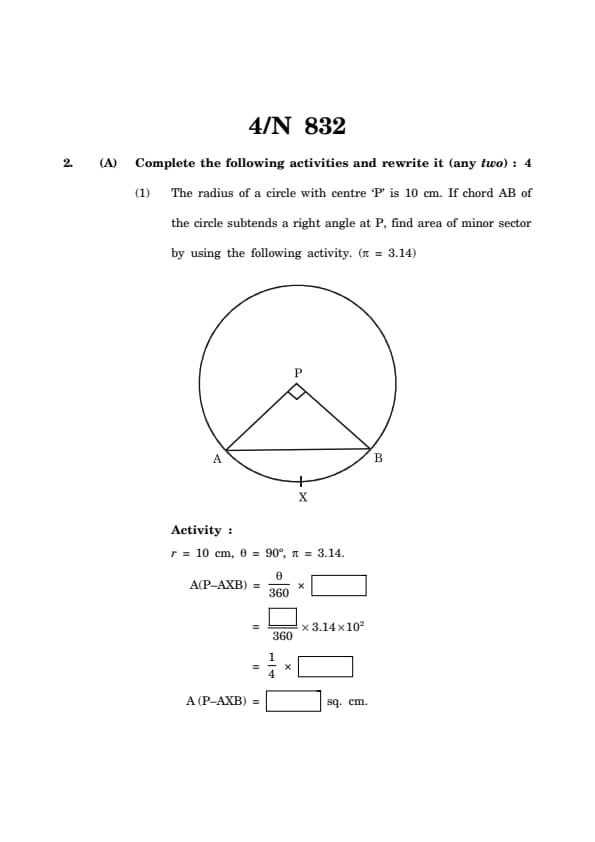
(1) The radius of a circle with centre 'P' is 10 cm. If chord AB of the circle subtends a right angle at P, find area of minor sector by using the following activity. (\(\pi = 3.14\))




Activity :

r = 10 cm, \(\theta\) = 90\(^\circ\), \(\pi\) = 3.14.

A(P-AXB) = \(\frac{\theta}{360} \times \framebox[1cm]{\phantom{X}}\)


= \(\frac{\framebox[1cm]{\phantom{X}}}{360} \times 3.14 \times 10^2\)


= \(\frac{1}{4} \times \framebox[1cm]{\phantom{X}}\)


A(P-AXB) = \framebox[1cm]{\phantom{X sq. cm.

In the following figure chord MN and chord RS intersect at point D. If RD = 15, DS = 4, MD = 8, find DN by completing the following activity:




Activity :
\(\therefore\) MD \(\times\) DN = \framebox[1cm]{\phantom{X \(\times\) DS.


 (Theorem of internal division of chords)

\(\therefore\) \framebox[1cm]{\phantom{X \(\times\) DN = 15 \(\times\) 4

\(\therefore\) DN = \(\frac{\framebox[1cm]{\phantom{X}}}{8}\)

\(\therefore\) DN = \framebox[1cm]{\phantom{X

An observer at a distance of 10 m from tree looks at the top of the tree, the angle of elevation is 60\(^\circ\). To find the height of tree complete the activity. (\(\sqrt{3} = 1.73\))



Activity :


In the figure given above, AB = h = height of tree, BC = 10 m, distance of the observer from the tree.


Angle of elevation (\(\theta\)) = \(\angle\)BCA = 60\(^\circ\)


tan \(\theta\) = \(\frac{\framebox[1cm]{\phantom{X}}}{BC}\) \dots \dots \dots (I)


tan 60\(^\circ\) = \framebox[1cm]{\phantom{X \dots \dots \dots (II)

\(\frac{AB}{BC} = \sqrt{3}\) \dots \dots (From (I) and (II))


AB = BC \(\times\) \(\sqrt{3}\) = 10\(\sqrt{3}\)


AB = 10 \(\times\) 1.73 = \framebox[1cm]{\phantom{X

\(\therefore\) height of the tree is \framebox[1cm]{\phantom{X m.

Solve the following sub-questions (any four):

(1) In \( \triangle ABC \), \( DE \parallel BC \). If \( DB = 5.4 \, cm \), \( AD = 1.8 \, cm \), \( EC = 7.2 \, cm \), then find \( AE \).

In the figure given below, find RS and PS using the information given in \(\triangle\)PSR.

In the following figure, circle with centre D touches the sides of \(\angle\)ACB at A and B. If \(\angle\)ACB = 52\(^\circ\), find measure of \(\angle\)ADB.

Verify, whether points, A(1, -3), B(2, -5) and C(-4, 7) are collinear or not.

If \(\sin\theta = \frac{11}{61}\), find the value of \(\cos\theta\) using trigonometric identity.

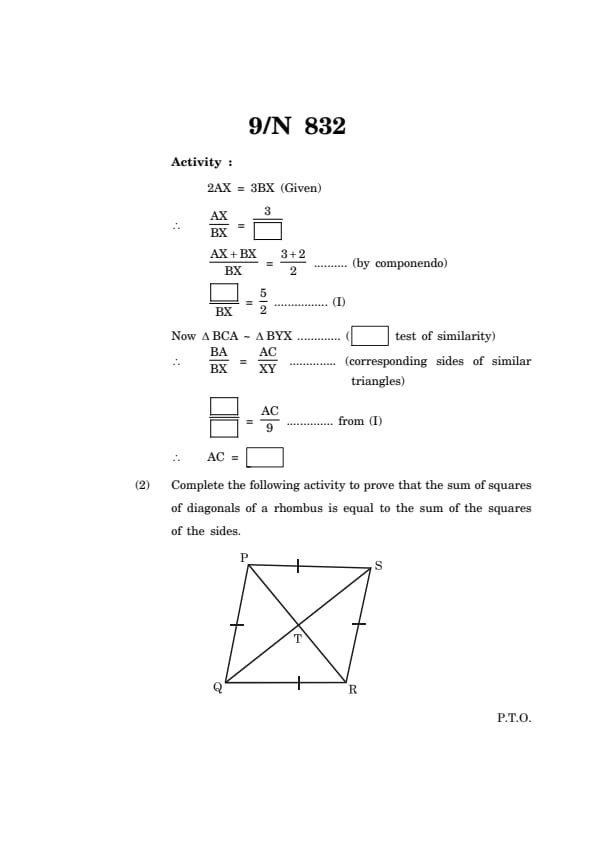
(1) In the following figure, XY \(||\) seg AC. If 2AX = 3BX and XY = 9. Complete the activity to find the value of AC.





Activity:


2AX = 3BX (Given)

\(\therefore \frac{AX}{BX} = \frac{3}{\framebox[1cm]{\phantom{X}}}\)

\(\frac{AX + BX}{BX} = \frac{3+2}{2}\) (by componendo)

\(\frac{BA}{BX} = \frac{5}{2}\) \dots \dots(I)


Now \(\triangle\) BCA \(\sim\) \(\triangle\) BYX (\framebox[1cm]{\phantom{X test of similarity)

\(\therefore \frac{BA}{BX} = \frac{AC}{XY}\) (corresponding sides of similar triangles)

\(\frac{5}{2} = \frac{AC}{9}\) from (I)

\(\therefore\) AC = \framebox[1cm]{\phantom{X

Complete the following activity to prove that the sum of squares of diagonals of a rhombus is equal to the sum of the squares of the sides.




Given: PQRS is a rhombus. Diagonals PR and SQ intersect each other at point T.


To prove: PS\(^2\) + SR\(^2\) + QR\(^2\) + PQ\(^2\) = PR\(^2\) + QS\(^2\)


Activity: Diagonals of a rhombus bisect each other.


In \(\triangle\)PQS, PT is the median and in \(\triangle\)QRS, RT is the median.

\(\therefore\) by Apollonius theorem,


PQ\(^2\) + PS\(^2\) = \framebox[1.5cm]{\phantom{X + 2QT\(^2\) \dots \dots(I)


QR\(^2\) + SR\(^2\) = \framebox[1.5cm]{\phantom{X + 2QT\(^2\) \dots \dots(II)


adding (I) and (II),


PQ\(^2\) + PS\(^2\) + QR\(^2\) + SR\(^2\) = 2(PT\(^2\) + \framebox[1.5cm]{\phantom{X) + 4QT\(^2\)


= 2(PT\(^2\) + \framebox[1.5cm]{\phantom{X) + 4QT\(^2\) (RT = PT)


= 4PT\(^2\) + 4QT\(^2\)


= (\framebox[1.5cm]{\phantom{X)\(^2\) + (2QT)\(^2\)

\(\therefore\) PQ\(^2\) + PS\(^2\) + QR\(^2\) + SR\(^2\) = PR\(^2\) + \framebox[1.5cm]{\phantom{X

Show that points P(1, -2), Q(5, 2), R(3, -1), S(-1, -5) are the vertices of a parallelogram.

Prove that tangent segments drawn from an external point to a circle are congruent.

Draw a circle with radius 4.1 cm. Construct tangents to the circle from a point at a distance 7.3 cm from the centre.

How many solid cylinders of radius 10 cm and height 6 cm can be made by melting a solid sphere of radius 30 cm?

(i) In the following figure DE\(||\)BC, then: If DE = 4 cm, BC = 8 cm, A(\(\triangle\)ADE) = 25 cm\(^2\), find A(\(\triangle\)ABC).

(ii) If DE : BC = 3 : 5, then find A(\(\triangle\)ADE) : A(\(\square\)DBCE).

\(\triangle\)ABC \(\sim\) \(\triangle\)PQR. In \(\triangle\)ABC, AB = 3.6 cm, BC = 4 cm and AC = 4.2 cm. The corresponding sides of \(\triangle\)ABC and \(\triangle\)PQR are in the ratio 2 : 3, construct \(\triangle\)ABC and \(\triangle\)PQR.

The radii of the circular ends of a frustum of a cone are 14 cm and 8 cm. If the height of the frustum is 8 cm, find: (\(\pi = 3.14\))
(i) Curved surface area of frustum.
(ii) Total surface area of the frustum.
(iii) Volume of the frustum.

(1) \(\square\)ABCD is a rectangle. Taking AD as a diameter, a semicircle AXD is drawn which intersects the diagonal BD at X. If AB = 12 cm, AD = 9 cm, then find the values of BD and BX.

(2) Taking \(\theta = 30^\circ\) to verify the following Trigonometric identities:
(i) \(\sin^2\theta + \cos^2\theta = 1\)
(ii) \(1 + \tan^2\theta = \sec^2\theta\)
(iii) \(1 + \cot^2\theta = \csc^2\theta\)